프로그래머스 소수 찾기

👉🏻문제 링크👈🏻

소수란?

1보다 큰 자연수 중, 1과 자기 자신 외에는 나누어지지 않는 수

소수 찾기 알고리즘

소수 찾기 알고리즘 두가지를 소개하려고 한다.

1. 직접 2부터 나눠서 나누어 떨어지는 수가 있는지 판별하는 방법

2. 어떤 수가 소수라면 그 값의 배수들을 모두 거짓으로 바꿔 걸러내는 방법

하나의 수가 주어지고 그 수가 소수인지 아닌지를 판별할 때에는 1번이 적합하고, 많은 수들 중에서 소수를 찾을 때에는 2번이 적합하다.

1. 나누어서 확인하기

특정 숫자 x이 소수인지 확인하는 가장 간단한 방법은 2에서부터 x-1까지 직접 나눠보고 나누어 떨어지는 수가 있는지 없는지 확인하는 방법이다.

def isPrime(x):
	for i in range(2, x):
    	if x % i == 0:
        	return False
    return True

그러나 자연수의 약수에 존재하는 원리를 생각하면 x-1까지 곱할 필요가 없다.

예를 들어 25의 약수는 1, 5, 25이다.

1 x 25 = 25
5 x 5 = 25
25 x 1 = 25

약수들이 대칭적으로 짝을 이루기 때문에 25의 제곱근을 기준으로 앞뒤는 똑같을 것이다.

그러므로 x의 제곱근까지만 나누어떨어지는지 확인하면 해당 숫자가 소수인지 아닌지 알 수 있다.

import math

def isPrime(x):
	for i in range(2, int(math.sqrt(x) + 1):
    	if x % i == 0:
        	return False
    return True

2. 소수가 아닌 수를 걸러내는 방법(에라토스테네스의 체)

sieve라는 0 ~ n까지의 숫자가 소수라면 True, 아니면 False의 값을 담고있는 배열을 생성한다. sieve[i]의 값이 참이라면 그 값의 배수들을 모두 거짓으로 바꾼다.

import math

def primeList(x):
	sieve = [False, False] + [True] * (x-1)
    for i in range(2, int(math.sqrt(x) + 1)):
    	if sieve[i] == True:
        	for j in range(2*i, x+1, i):
            	sieve[j] = False
    return [i for i in range(n) if sieve[i] == True]

문제 풀이

이 문제에서는 2번 방법으로 풀이하는 것이 좋을 것 같다.
itertools를 활용하면 순열을 쉽게 구할 수 있다.

from itertools import permutations
permutations(p, r)

p: 순열을 뽑을 iterable한 객체
r: 순열의 길이. 지정하지 않았을 경우 iterable의 길이
순열로 뽑은 숫자들 중 가장 큰 숫자의 제곱근을 기준으로 2번 방법을 진행한다.

import math
from itertools import permutations

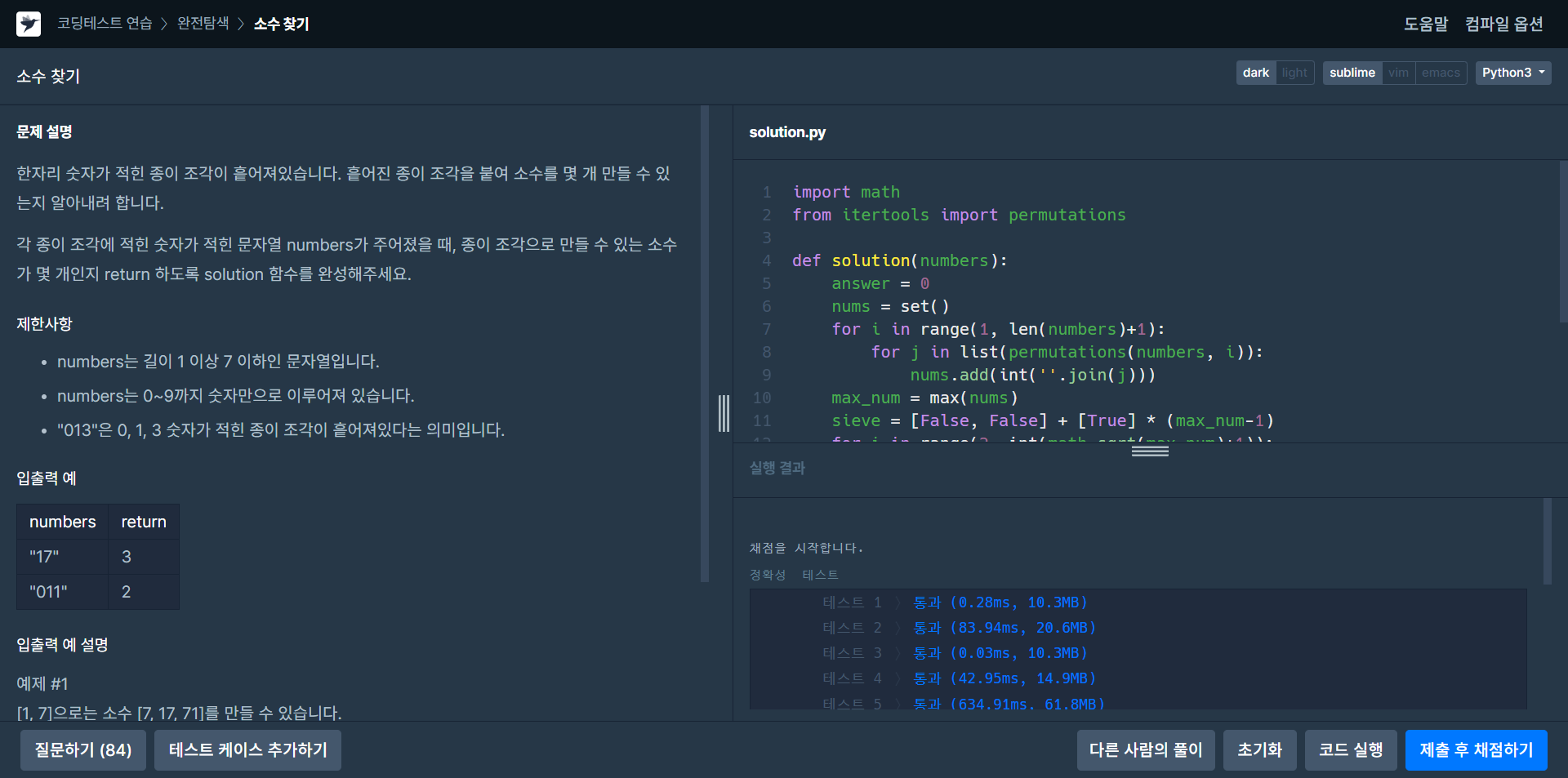
def solution(numbers):
    answer = 0
    nums = set()
    for i in range(1, len(numbers)+1):
        for j in list(permutations(numbers, i)):
            nums.add(int(''.join(j)))
    max_num = max(nums)
    sieve = [False, False] + [True] * (max_num-1)
    for i in range(2, int(math.sqrt(max_num)+1)):
        if sieve[i] == True:
            for j in range(2*i, max_num+1, i):
                sieve[j] = False
    lst_nums = list(nums)
    for num in lst_nums:
        if sieve[num]:
            answer += 1
    return answer