[자료구조] stack과 queue

Jifrozen·2022년 10월 3일
0

기초 다지기

목록 보기
6/29
post-custom-banner

stack

가장 마지막으로 들어간 데이터가 가장 첫 번째로 나오는 성질(LIFO : 후입선출)을 가진 자료구조이다.
삽입 및 삭제 O(1) 탐색 O(n)

언제 사용?
재귀, 웹 브라우저 방문 기록, 역순 출력, 후위 표기법

java에서 스택 선언

Stack st=new Stack();

구현

push와 pop할 때는 해당 위치를 알고 있어야 하므로 기억하고 있는 '스택 포인터(SP)'가 필요함

스택 포인터는 다음 값이 들어갈 위치를 가리키고 있음 (처음 기본값은 -1)

private int sp = -1;

데이터 넣음 : push()

public void push(Object o) {
    if(isFull(o)) {
        return;
    }
    
    stack[++sp] = o;
}

데이터 최상위 값 뺌 : pop()

public Object pop() {
    
    if(isEmpty(sp)) {
        return null;
    }
    
    Object o = stack[sp--];
    return o;
    
}

비어있는 지 확인 : isEmpty()

private boolean isEmpty(int cnt) {
    return sp == -1 ? true : false;
}

꽉차있는 지 확인 : isFull()

private boolean isFull(int cnt) {
    return sp + 1 == MAX_SIZE ? true : false;
}

MAX_SIZE 없이 동적 배열 스택 만들기
최대 크기가 없는 스택을 만드려면? 2가지 해결 방법 존재

  1. arraycopy를 활용한 동적배열 사용
public void push(Object o) {
    
    if(isFull(sp)) {
        
        Object[] arr = new Object[MAX_SIZE * 2];
        // stack의 인덱스 0부터 MAX_SIZE만큼을 arr 배열의 0번째부터 복사
        System.arraycopy(stack, 0, arr, 0, MAX_SIZE);
        //배열 arr의 참조값을 stack에 덮어씌운다 -> stack 배열은 이제 arr배열을 가리킴
        stack = arr;
        MAX_SIZE *= 2; // 2배로 증가
    }
    
    stack[sp++] = o;
}
  1. 스택을 연결리스트로 구현
public class Node {

    public int data;
    public Node next;

    public Node() {
    }

    public Node(int data) {
        this.data = data;
        this.next = null;
    }
}
public class Stack {
    private Node head;//현재 위치 확인하기 위해+next만 있고 prev는 없어서 필요
    private Node top;

    public Stack() {
        head = top = null;
    }

    private Node createNode(int data) {
        return new Node(data);
    }

    private boolean isEmpty() {
        return top == null ? true : false;
    }

    public void push(int data) {
        if (isEmpty()) { // 스택이 비어있다면
            head = createNode(data);
            top = head;
        }
        else { //스택이 비어있지 않다면 마지막 위치를 찾아 새 노드를 연결시킨다.
            Node pointer = head;

            while (pointer.next != null)
                pointer = pointer.next;

            pointer.next = createNode(data);
            top = pointer.next;
        }
    }

    public int pop() {
        int popData;
        if (!isEmpty()) { // 스택이 비어있지 않다면!! => 데이터가 있다면!!
            popData = top.data; // pop될 데이터를 미리 받아놓는다.
            Node pointer = head; // 현재 위치를 확인할 임시 노드 포인터

            if (head == top) // 데이터가 하나라면
                head = top = null;
            else { // 데이터가 2개 이상이라면
                while (pointer.next != top) // top을 가리키는 노드를 찾는다.
                    pointer = pointer.next;

                pointer.next = null; // 마지막 노드의 연결을 끊는다.
                top = pointer; // top을 이동시킨다.
            }
            return popData;
        }
        return -1; // -1은 데이터가 없다는 의미로 지정해둠.

    }

}

Queue

큐는 먼저 집어넣은 데이터가 먼저 나오는 성질(FIFO 선입선출)을 지닌 자료구조이다.
삽입 및 삭제 O(1) 탐색 O(n)

언제 사용?
버퍼, 마구 입력된 것을 처리하지 못하고 있는 상황, BFS, CPU 작업을 기다리는 프로세스, 스레드 행렬 또는 네트워크 접속 기다리는 행렬, 캐시

자바에서 큐 선언

Queue q=new LinkedList<>();

구현

큐의 가장 첫 원소를 front, 끝 원소를 rear라고 부름

큐는 들어올 때 rear로 들어오지만, 나올 때는 front부터 빠지는 특성을 가짐

접근방법은 가장 첫 원소와 끝 원소로만 가능

데이터를 넣고 뺄 때 해당 값의 위치를 기억해야 함. (스택에서 스택 포인터와 같은 역할)

이 위치를 기억하고 있는 게 front와 rear

front : deQueue 할 위치 기억

rear : enQueue 할 위치 기억

private int size = 0; 
private int rear = -1; 
private int front = -1;

Queue(int size) { 
    this.size = size;
    this.queue = new Object[size];
}

데이터 넣음 : offer()

public void offer(Object o) {
    
    if(isFull()) {
        return;
    }
    
    queue[++rear] = o;
}

데이터 뺌 : poll()

public Object poll(Object o) {
    
    if(isEmpty()) { 
        return null;
    }
    
    Object o = queue[front];
    queue[front++] = null;
    return o;
}

비어있는 지 확인 : isEmpty()

public boolean isEmpty() {
return front == rear;
}

꽉차있는 지 확인 : isFull()

public boolean isFull() {
return (rear == queueSize-1);
}

문제점
front 는 남아있는데 rear가 끝에 도달했을때 메모리가 꽉 차있다고 판단
-> 이를 개선한 것 원형 큐

원형큐

논리적으로 배열의 처음과 끝이 연결되어 있는 것으로 간주함!

원형 큐는 초기 공백 상태일 때 front와 rear가 0

공백, 포화 상태를 쉽게 구분하기 위해 자리 하나를 항상 비워둠

(index + 1) % size로 순환시킨다
private int size = 0; 
private int rear = 0; 
private int front = 0;

Queue(int size) { 
    this.size = size;
    this.queue = new Object[size];
}

public void offer(Object o) {
    
    if(isFull()) {
        return;
    }
    
    rear = (++rear) % size;
    queue[rear] = o;
}

public Object poll(Object o) {
    
    if(isEmpty()) { 
        return null;
    }
    
    preIndex = front;
    front = (++front) % size;
    Object o = queue[preIndex];
    return o;
}

public boolean isEmpty() {
    return front == rear;
}

public boolean isFull() {
    return ((rear+1) % size == front);
}

원형 큐의 단점 : 메모리 공간은 잘 활용하지만, 배열로 구현되어 있기 때문에 큐의 크기가 제한

이를 개선한 것이 연결리스트 큐

연결리스트 큐

연결리스트 큐는 크기가 제한이 없고 삽입, 삭제가 편리
자바에서 큐는 연결리스트를 이용하여 구현되어있다.
삽입은 tail, 제거는 head로 하면서 삽입/삭제를 스택처럼 O(1)에 가능하도록 구현이 가능.

public void enqueue(E item) {
    Node oldlast = tail; // 기존의 tail 임시 저장
    tail = new Node; // 새로운 tail 생성
    tail.item = item;
    tail.next = null;
    if(isEmpty()) head = tail; // 큐가 비어있으면 head와 tail 모두 같은 노드 가리킴
    else oldlast.next = tail; // 비어있지 않으면 기존 tail의 next = 새로운 tail로 설정
}
  • 데이터 추가는 끝 부분인 tail에 한다.
  • 기존의 tail는 보관하고, 새로운 tail 생성
  • 큐가 비었으면 head = tail를 통해 둘이 같은 노드를 가리키도록 한다.
  • 큐가 비어있지 않으면, 기존 tail의 next에 새로만든 tail를 설정해준다.
public T dequeue() {
    // 비어있으면
    if(isEmpty()) {
        tail = head;
        return null;
    }
    // 비어있지 않으면
    else {
        T item = head.item; // 빼낼 현재 front 값 저장
        head = head.next; // front를 다음 노드로 설정
        return item;
    }
}
  • 데이터는 head로부터 꺼낸다. (가장 먼저 들어온 것부터 빼야하므로)
  • head의 데이터를 미리 저장해둔다.
  • 기존의 head를 그 다음 노드의 head로 설정한다.
  • 저장해둔 데이터를 return 해서 값을 빼온다.

PriorityQueue

Queue 인터페이스의 구현체 중 하나로, 저장한 순서에 관계없이 우선순위가 높은 것부터 꺼내게 된다는 특징이 있다.

기본적으로 PriorityQueue는 낮은것부터 반환해주지만 Comparable Interface를 구현하면 우선순위의 기준을 정해 리턴이 가능하다. compareTo method를 override 하게 되고 해당 객체에서 처리할 우선순위 조건을 리턴해주면 PriorityQueue 가 알아서 우선순위가 높은 객체를 추출한다.

PriorityQueue<Integer> priorityQueueLowest = new PriorityQueue<>(new Comparator<int>() {
	@Override
	public int compare(int o1, int o2) {
		int o1Result = o1*o1;
		int o2Result = o2*o2;
		return o1Result-o2Result;
	}
});

PriorityQueue는 Heap을 이용하여 구현하는 것이 일반적이다.

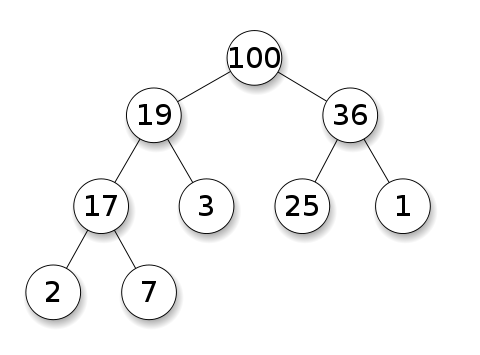
  • 데이터의 정렬, 검색이 아닌 우선순위의 데이터 검색과 삭제에 유용한 자료구조
  • 데이터를 삽입할 때 우선순위를 기준으로 최대 힙 혹은 최소 힙을 구성하고 데이터를 꺼낼 때 루트 노드를 얻어낸 뒤 루트 노드를 삭제할 때는 빈 루트 노드 위치에 맨 마지막 노드를 삽입한 후 아래로 내려가면서 적절한 자리를 찾아 옮기는 방식으로 진행된다.
  • 최대 값이 우선순위인 큐 = 최대 힙, 최소 값이 우선순위인 큐 = 최소 힙

Priority Queue 특징

  1. 높은 우선순위의 요소를 먼저 꺼내서 처리하는 구조이다.
    우선순위 큐에 들어가는 원소는 비교가 가능한 기준이 있어야한다.

  2. 내부 요소는 힙으로 구성되어 이진트리 구조로 이루어져 있다.

  3. 내부구조가 힙으로 구성되어 있기에 시간 복잡도는 O(NLogN)이다.

  4. 우선순위를 중요시해야 하는 상황에서 주로 쓰인다.

힙

힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조

특징

  • 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
  • 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어짐
  • 힙은 일종의 반정렬 상태를 유지
    - 큰 값이 상위 작은 값이 하위에 있는 정도
  • 중복 값 허용
  • O(logN)

종류

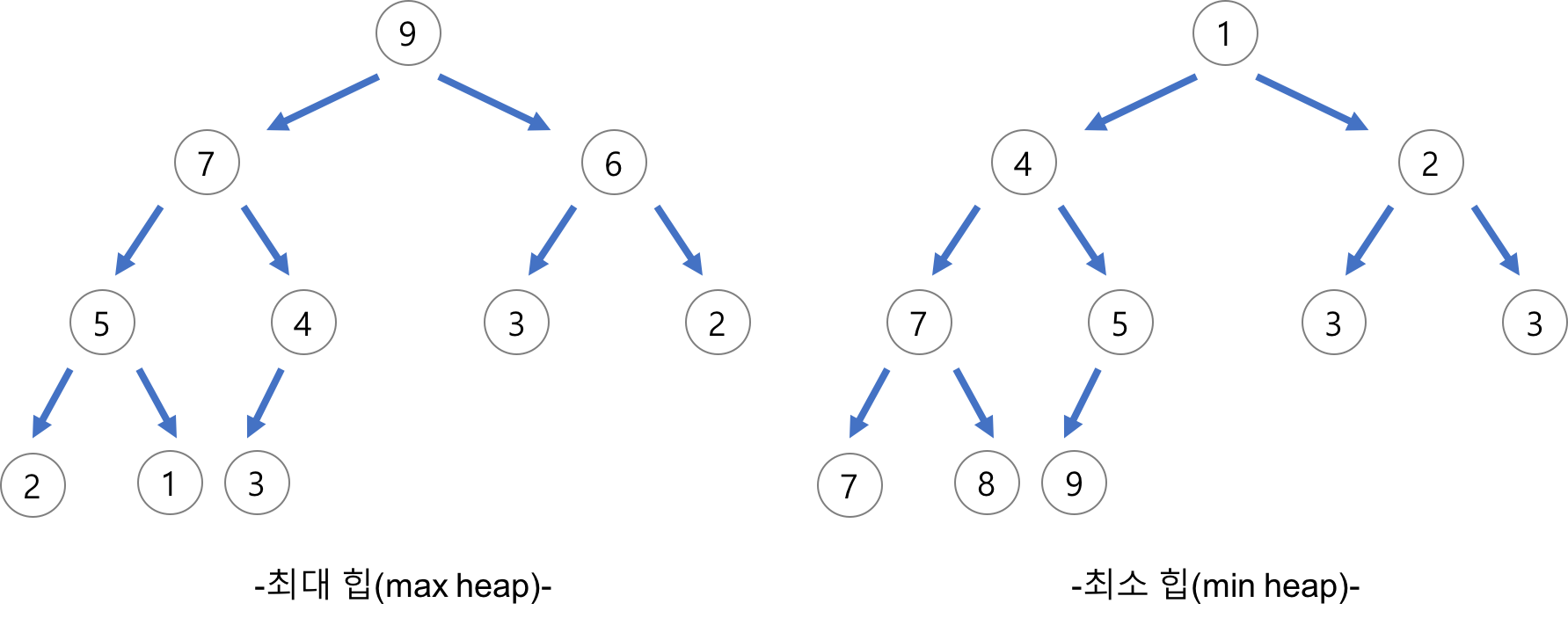
힙의 삽입

부모와 비교해서 크면(작으면) 부로 노드와 교환

힙의 삭제

최대값이나 최소값을 꺼내기 때문에 루트 노드 삭제
-> 마지막 노드 가져와서 루트 노드로 삽입 -> 자식 노드와 비교하며 교환됨

Deque(Double-Ended Queue)


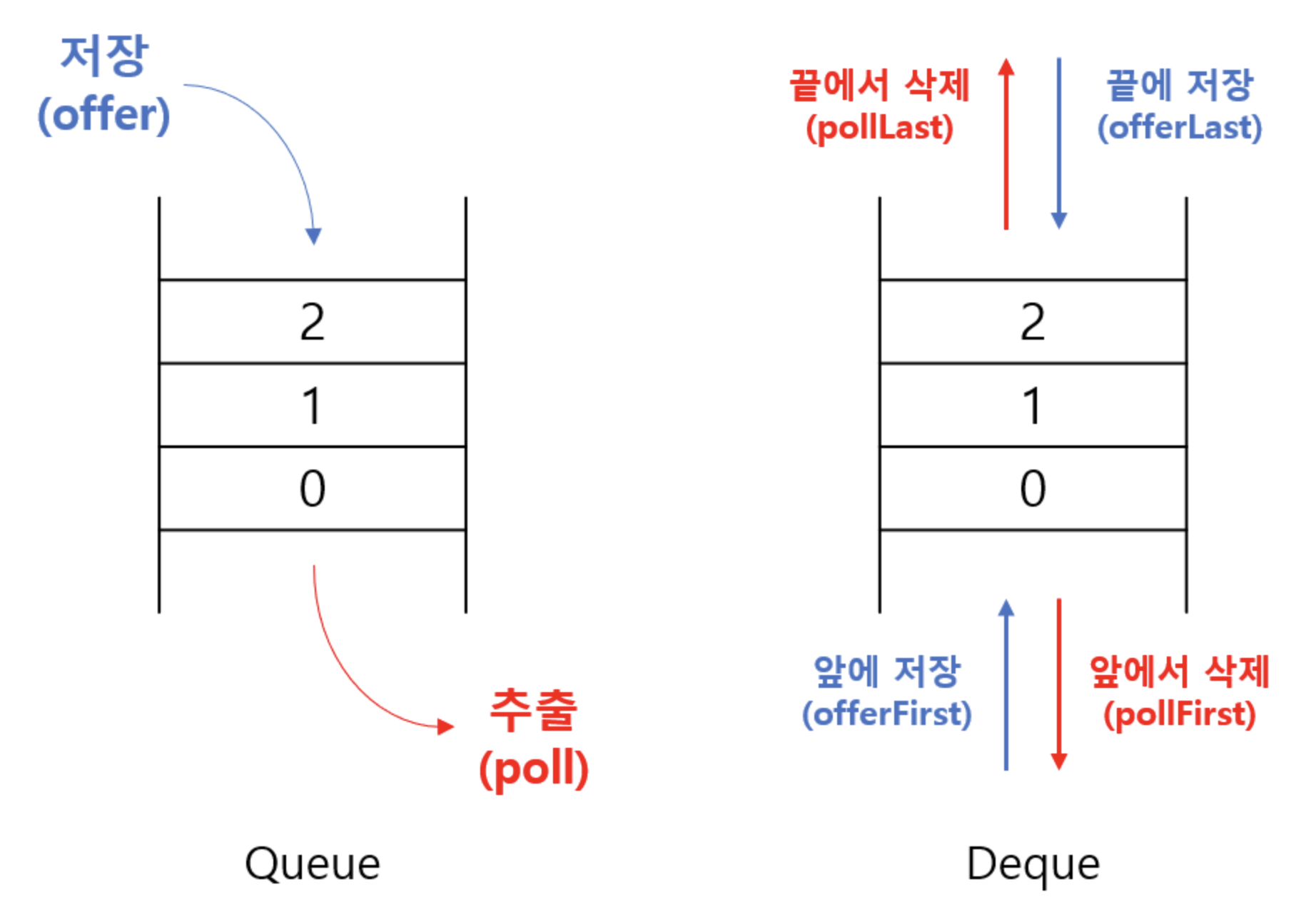
Queue 변형으로, 한쪽 끝으로만 추가/삭제 할 수 있는 Queue와 달리, Deque는 양쪽 끝에서 추가/삭제가 가능하다.(따라서 Stack으로도 queue로도 쓰일 수 있다.) Deque의 조상은 Queue이며, 구현체로는 ArratDqeue와 LinkedList등이 있다.

ArrayDeque<Integer> dq = new ArrayDeque<Integer>();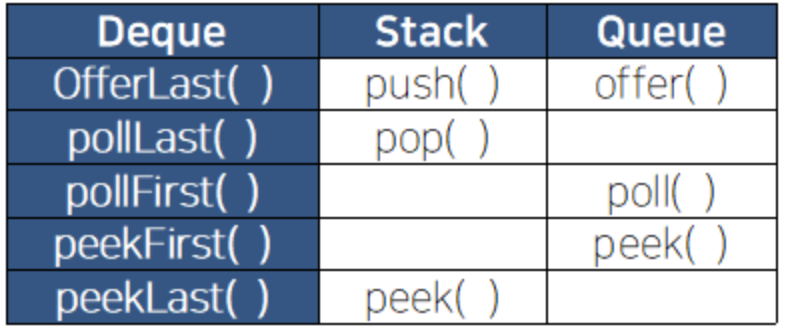

출처
https://gyoogle.dev/blog/computer-science/data-structure/Stack%20&%20Queue.html
https://pridiot.tistory.com/68
https://velog.io/@gillog/Java-Priority-Queue우선-순위-큐
https://blog.advenoh.pe.kr/java/자바-자료구조-Priority-Queue-우선순위-큐/
https://ynzu-dev.tistory.com/entry/JAVA-Priority-Queue우선순위-큐-우선순위-조건-변경하기
https://velog.io/@agugu95/Java-Heap-Binary-Heap

profile
Jifrozen
이전 포스트

[JAVA] JVM 구성요소 - 메모리 영역

다음 포스트

[프로젝트] Micro Services Architecture

post-custom-banner

0개의 댓글