목표

• Heap 자료구조에 대해서 알아본다
• Heap 자료구조를 구현해본다.
• Heap 자료구조를 통해 구현할 수 있는 우선순위 큐를 알아본다.

Heap

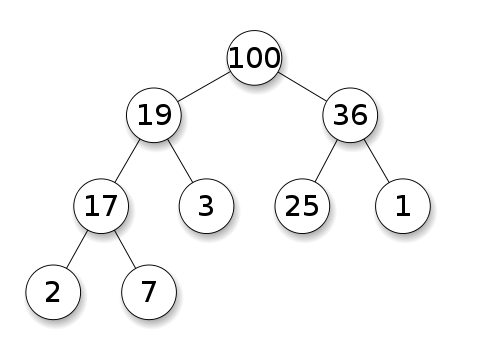
• Priority Queue를 구현하기 위한 자료구조
• 데이터의 정렬, 검색이 아닌 우선순위의 데이터 검색과 삭제에 유용한 자료구조
• 일반적으로 Binary Heap을 구현하여 사용
• Heap sort, Graph, Priority Queue 등에 쓰인다

Binary Heap

• 완전 이진트리 방식을 통해 자료구조를 구현
• 중복된 값이 존재할 수 있음 (데이터의 검색이 아닌 최대, 최소값이 목적)
• 보통 힙의 구현은 배열로 이루어진다.
• 힙은 최대값, 최소값 검색에 대해 $log N$의 굉장히 빠른 속도를 가진다. (루트만 반환, 삭제하면 됨)

Max Heap

• 이진 힙의 구현 방식에서 최대값을 위한 구조
• 루트는 모든 자식 노드보다 크거나 같다.

Min Heap

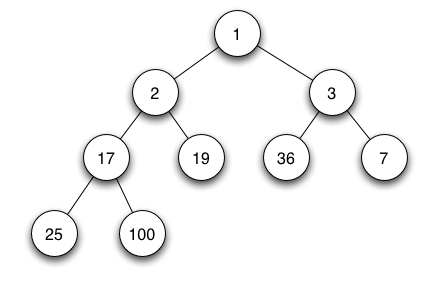
• 이진 힙의 구현 방식에서 최소값을 위한 구조
• 루트는 모든 자식노드보다 작거나 같다.

Heap 구현

1. 완전 이진트리를 만든다.
2. 삽입
3. 힙의 조건을 만족하지 못하면 스왑
4. 3을 반복시 루트는 최대, 최소의 힙이 된다.

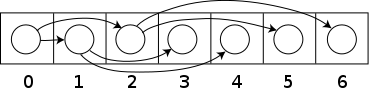
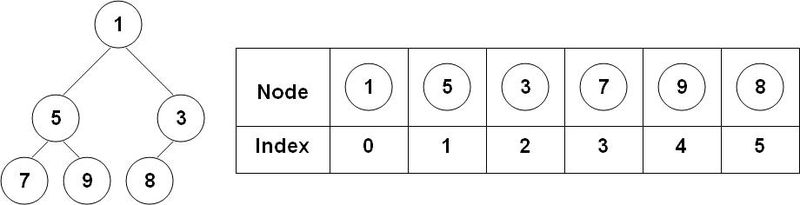
힙 구현

• 트리의 좌, 우측과 부모 노드를 알기 위한 메소드

private int parent(int pos) {
        return pos / 2;
    }
private int leftChild(int pos) {
        return (2 * pos);
    }

private int rightChild(int pos) {
        return (2 * pos) + 1;
    }

private boolean isLeaf(int pos) {
        return pos >= (size / 2) && pos <= size;
    }

• 데이터 삽입 시 바로 힙의 조건 판단 후 스왑

 public void insert(int input) {
        maxHeap[++size] = input;
        int current = size;
        while (maxHeap[current] > maxHeap[parent(current)]) {
            swap(current, parent(current));
            current = parent(current);
        }
    }

• 힙 삭제 시 재조정을 위한 재귀함수

private void maxHeapify(int pos) {
        if (isLeaf(pos)) {
            return;
        }
        if (maxHeap[pos] < maxHeap[leftChild(pos)]
                || maxHeap[pos] < maxHeap[rightChild(pos)]) {
            if (maxHeap[leftChild(pos)] > maxHeap[rightChild(pos)]) {
                swap(pos, leftChild(pos));
                maxHeapify(leftChild(pos));
            } else {
                swap(pos, rightChild(pos));
                maxHeapify(rightChild(pos));

            }
        }
    }

util.PriorityQueue를 통한 힙 구현

PriorityQueue<Integer> p = new PriorityQueue<>();

        p.add(10);
        p.add(30);
        p.add(400);
        p.add(5);
        p.add(347);

        System.out.println(p.peek()); // 400

• Collections.reversOrder() 시 최대 힙, 오름차순 정렬 시 최대 힙 구현

Priority Queue

• 우선순위 큐로 데이터 중에서 우선순위가 높은 데이터를 빠르게 알 수 있다.
• 큐와 연산이 동일하나 우선순위가 가장 높은 데이터를 알 수 있다.
  이를 통해 최대 힙과 최소 힙을 구현 가능하다.

  최대 값이 우선순위인 큐 = 최대 힙, 최소 값이 우선순위인 큐 = 최소 힙

• 우선순위 큐를 통해 데이터를 정렬하는 것이 heap sort

우선순위 큐 구현

• 자바에서는 Priority Queue <E> 클래스로 우선순위 큐를 구현
• AbstractQueue Abstract Class를 구현
  • peek, element
  • poll, remove
  • add, offer
  • isEmpty
• Collection 프레임워크

백준 11279 최대 힙
public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int input = sc.nextInt();
        int data = 0;
        if (input != 0 && input < 100001) {
            PriorityQueue<Integer> pq = new PriorityQueue<>(1000000, Collections.reverseOrder());
            while (input != 0) {
                data = sc.nextInt();
                if (data != 0) {
                    pq.add(data);
                } else {
                    if (pq.peek() == null) {
                        System.out.println(0);
                    } else {
                        System.out.println(pq.poll());
                    }
                }
                input--;
            }
        }
    }

참고

영문위키
Geek for Geeks