- 3Blue1Brown 유튜뷰 | 'Essence of linear algebra'의 내용을 요약
- 선형대수학을 고등학교때 배운 문제풀이 skill 로서가 아닌, 수식의 배경과 의미 그리고 그 변화를 기하학적인 관점으로 공부하는 것에 의의가 있는 것 같다. 수학적 풀이로서만 접근하면 쉬워보일 수 있겠지만, 그것이 무엇을 의미하는지 본질을 파악하고 넘어가자 ! ! !
- 내가 이해할 수 있는 나의 언어로 기록하기
1. Essence of linear algebra
-
벡터(vector)
- 물리학 관점 : 공간에서의 화살표. 길이와 방향이 같다면 이동해도 같은 벡터임. 평평한 평면 벡터는 2차원 ... n차원 벡터
- 컴퓨터 과학 관점 : 순서가 중요한 숫자의 리스트
- 수학 관점 : 무엇이든 벡터가 될 수 있음. 두 벡터를 합해도, 곱해도 여전히 벡터 ~
- 공부하면서 : 수학적인 관점으로, 벡터 (x, y)라고 하면 원점에서의 x, y 좌표를 상상하자. 모든 숫자쌍은 하나의 벡터와 대응되고, 모든 벡터는 각 대응된은 숫자쌍이 있다.
-
벡터의 연산
-
벡터의 합

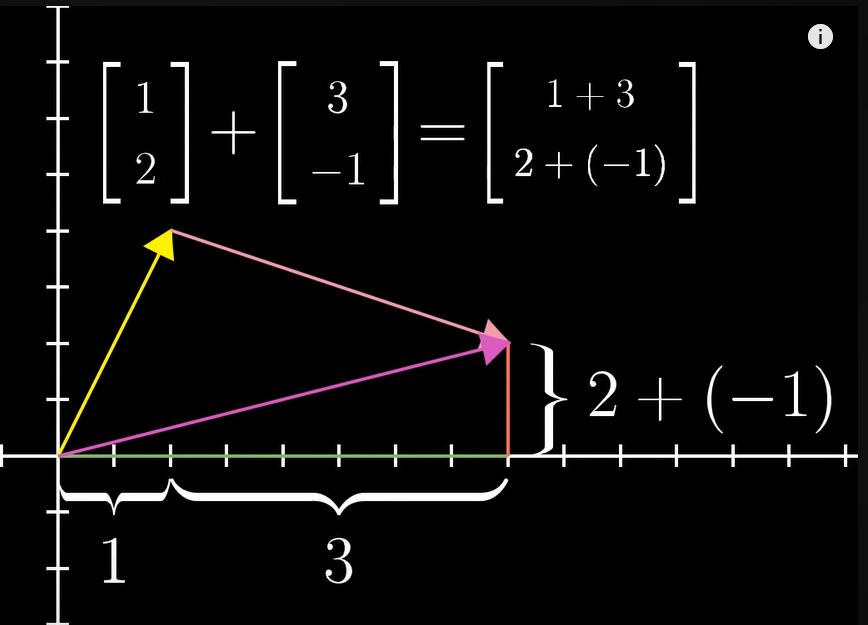
-
벡터의 곱
: 벡터의 길이를 늘이거나 줄이거나, 방향을 뒤집는 것 = 스케일링(scaling)
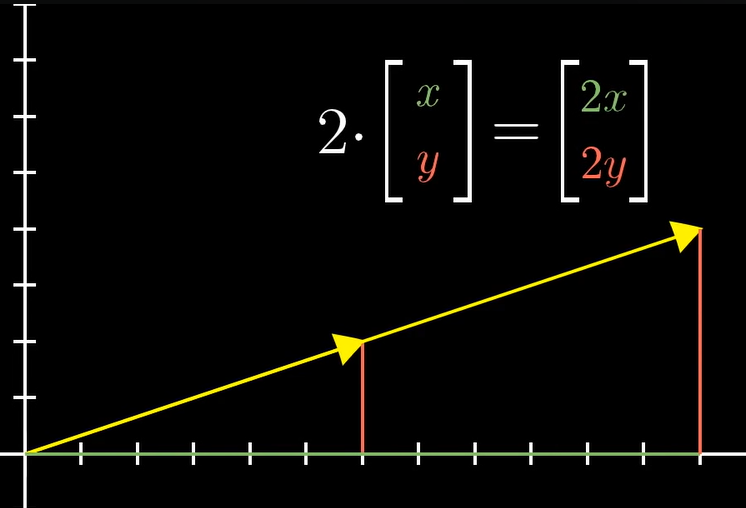 벡터를 변형시키는 정도를 스칼라(Scalars)라고 하며, 벡터에 스칼라 곱을 한다고 표현. - 캡쳐 속 스칼라 : 2, 벡터 : (3,1)
벡터를 변형시키는 정도를 스칼라(Scalars)라고 하며, 벡터에 스칼라 곱을 한다고 표현. - 캡쳐 속 스칼라 : 2, 벡터 : (3,1)
-
2. Linear combination, span and basis vectors
-
단위벡터(unit vector)
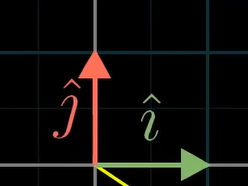
-
단위벡터는 크기가 1인 벡터를 말한다.
-
x축 단위벡터 :
-
y축 단위벡터 :
-
위 단위벡터는 좌표계의 '기저'임. 기저벡터(basic vectors)는 스칼라가 스케일하는 대상이다.
-
기저벡터는 단위벡터 중 하나이다.
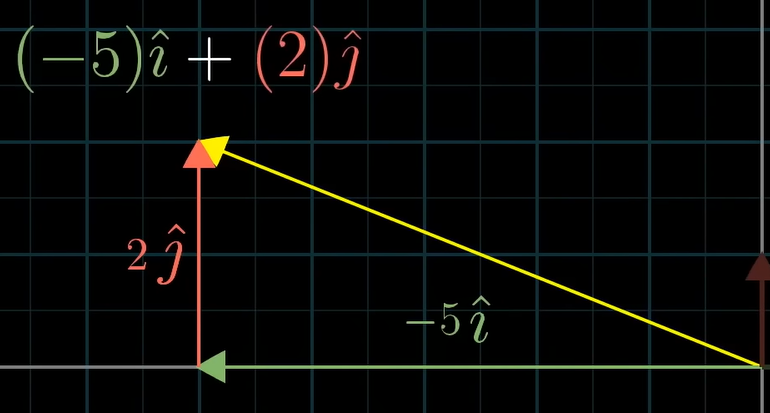
는 -5(스칼라)가 (x축 단위벡터이자 기저벡터)를, 2(스칼라)가 (y축 단위벡터이자 기저벡터)를 스케일링한 것이다.
-
2차원에 표현할 수 있는 벡터들은 기저벡터로 모두 표현할 수 있다.
-
-
선형조합(linear combination)
-
두 벡터를 스케일링하고 나서 더하는 것을 두 벡터의 선형조합이라고 한다.
-
(두 벡터가 서로 선형독립적이거나 행렬식이 0이 아니라면) 2차원에 표현할 수 있는 벡터들은 기저벡터 혹은 단위벡터의 선형조합으로 모두 표현할 수 있다.
-
- span
- 벡터들이 만들 수 있는 모든 선형조합의 결과
- 2차원
- 두 벡터가 서로 선형독립 & 행렬식이 0 => 2차원의 모든 좌표를 의미
- 두 벡터가 서로 선형종속 => 선(line)을 의미
- 3차원
- 두 벡터 서로 선형독립 & 행렬식이 0 => 원점을 지나는 평면 좌표를 의미
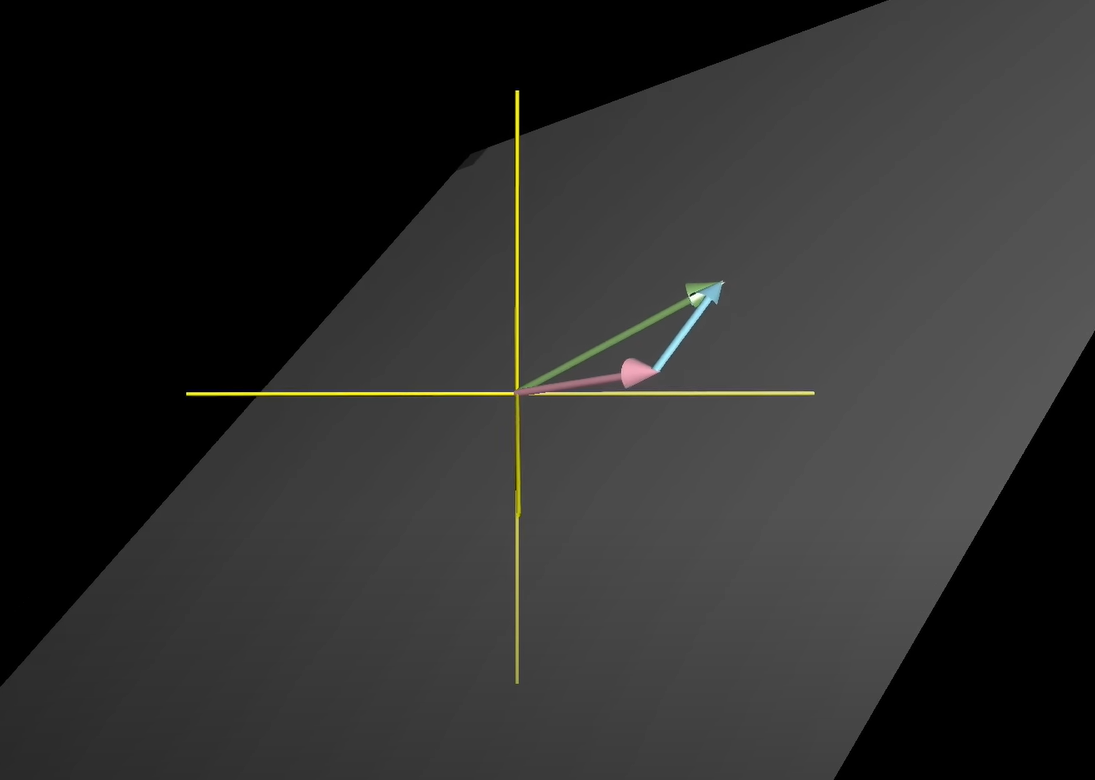
- 세 벡터가 모두 선형 독립 => 3차원의 모든 좌표
- 두 벡터 서로 선형독립 & 행렬식이 0 => 원점을 지나는 평면 좌표를 의미
3. Linear transformation and matrices
-
선형 변환(linear transformation)
-
input 벡터를 output 벡터로 바꾸는 변환식과 같은 것
-
function 대신 transformation이라고 하는 이유는, input 벡터의 위치를 '옮겨서' output 벡터로 변형하는 느낌을 주기 때문이다.
-
변환 이후에도 선형이어야 하며, 평행하고 동일한 간격으로 있어야 하며, 원점은 변환 이후에도 여전히 원점이다.
-
이를 수식으로 구하는 방법은 input 벡터인 기저 벡터(, )가 어떻게 변화하는지만 구하면 된다.
- = = -1+2
-
변환 전에 v벡터를 이루는 과 의 어떤 선형결합은 변환 후에도 같은 선형결합을 유지한다.
-
= -1*( ) + 2*( )
-
만약 = (1, -2)이고, = (3,0) 이라면,
= -1 + 2 =
-
다르게 표현하면,
= =즉, 기저벡터의 도착점만 안다면 선형변환 후의 벡터(output vector)를 구할 수 있다.
-
-
= ,
= ,
= 라면,
=
-
한 행렬은 하나의 선형변환을 의미한다. 벡터에 행렬을 곱하는 것은 수식적으로 그 벡터를 선형변환하는 것이다.
-
= 라는 것은,
가 A만큼 선형변환하여 가 된다는 것.
-
라는 것은,
가 (a, b)로, 가 (c,d)로 움직인 다음
(a, b)는 배, (c, d)는 배로 스케일링 된 후,
결합된다는 것. -
= 에서 x와 y란,
가 (a, b)로, 가 (c, d)로 선형변환될 때, (e, f)로 선형변환되는 기저벡터 (x, y)가 무엇인가를 찾는 것.
-
4. Matrix multiplication as composition and Three-dimensional linear transformations
- 합성 행렬(Matrix multiplication) : 행렬의 곱, 행렬의 결합(composition). 기저벡터를 한 번 선형변환하고 나서 다른 변환을 한 번 더 적용한 것
-
란, 기저벡터가 B만큼 선형변환된 후, A가 적용되어 선형변환되는 것이다.
-
AB != BA 인 이유를 수식으로 설명하는 것이 아닌, 머릿속에서 이미지화하여 생각한다면 쉽다.
-
기저벡터를 90도 회전하고 옆으로 기울이는 것(shear)과, 옆으로 기울이고(shear) 90도로 회전하는 것은 다르다.
- 참고 : 기울이기(shear) 변환을 나타내는 행렬은 이다. 는 움직이지 않고, 만 (1,1)로 움직인다.
-
3차원 행렬 또한 마찬가지
6. The determinant
-
2차원에서 선형변환이 일어날 때, 격자선이 평행하고 균등한 거리를 유지하기 때문에, 벡터가 만들어내는 공간의 변환 정도 역시 동일하다.
-
행렬식(determinant) : 선형변환에 의한 영역(공간)의 변화를 나타내는 요인.
-
의 행렬식은 라고 표현한다.
= 일 때, = ad - bc 이다.
-
행렬식 양수 k라면 벡터 영역의 크기가 k배 만큼 변화한다는 것, 음수 k라면 영역의 크기 자체는 k배만큼 커지지만 방향이 반대임.
-
행렬식이 음수가 되어 방향이 변환하는 것을 invert the orientation of space 라고 부른다.
-
원래 왼쪽에 가 있는데,
선형변환 이후 의 오른쪽에 가 있게 된다면, 이는 orientation of space가 inverted 되었다고 한다.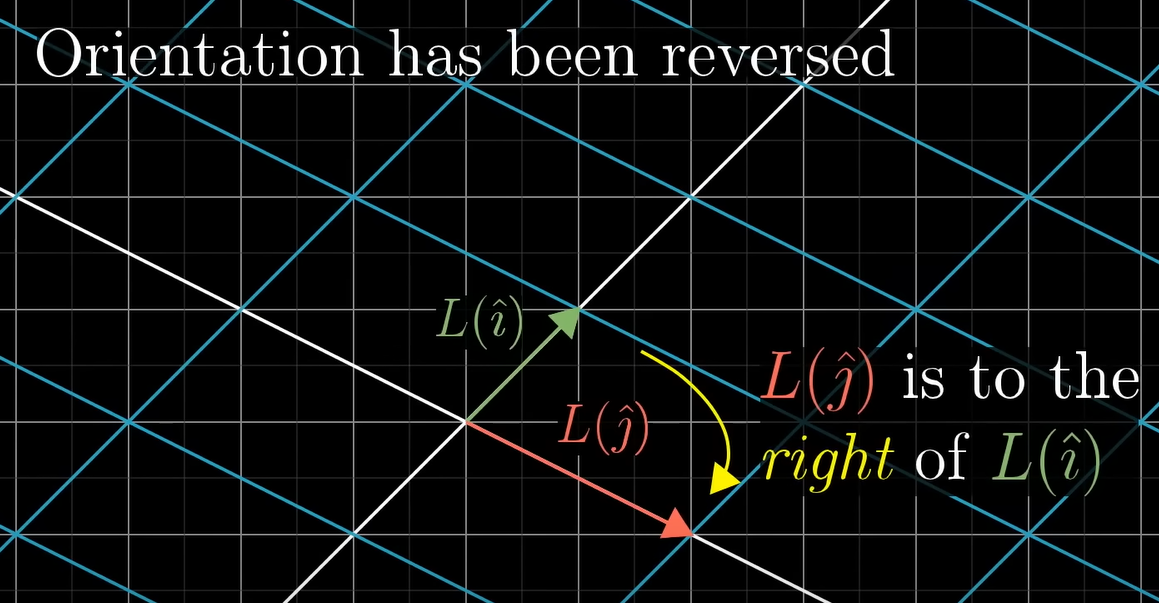
이때 행렬식은 항상 음수값을 가지며, 절댓값만큼 공간(영역)이 스케일된다.
-
행렬식이 0이라는 것은, 공간이 찌부되어 점 혹은 선을 이룬다는 것이다. 즉, 선형종속이 된다는 뜻.
-
-
3차원에서의 행렬식은 부피로서의 공간 변화를 나타낸다. 행렬식이 0이라면 선형변환 후 평면, 선, 점이 된 것. (선형종속)
7. Inverse matrices, column space and null space
-
역행렬 : != 0 일때 존재
- 일대일 대응 변환 : 의 역행렬은 하나뿐이다.
- 항등 변환 : * 의 결과값은 아무것도 하지 않은 과 됨. = 단위행렬 이 된다는 것.
- = 이라면, =
-
rank : 선형변환의 결과가 n차원이라면, rank는 n이다. 행렬의 선형 독립인 column vector의 갯수이다. column space의 차원의 수임.
-
column space : 행렬의 선형 독립인 기저벡터가 선형 조합으로 만들 수 있는 부분 공간. 3차원 공간에서 rank가 2일 경우, column space는 2차원 평면이 된다.
-
영공간(null space)(=kernel) : 선형변환의 결과가 영벡터가 되게 하는 벡터의 해집합.
= 에서 가 영벡터인 경우, 해()는 모든 null space가 될 수 있다.
8. Nonsquare matrices as transformations between dimensions
-
X 행렬에서, : input 기저 벡터의 수, : 기저벡터의 변환 후 좌표값 개수(차원(
-
X 행렬은 2차원 평면이 3차원상에 나타나는 것.
X 행렬은 3차원 공간이 2차원으로 찌그러져 축소되는 것.
9. Dot products and duality
-
내적(Dot products)
-
두 벡터의 내적이란, 각 인덱스에 대응하는 원소를 곱한 뒤 더하여 하나의 스칼라 값으로 만들어 주는 연산
*
-
이는 행렬과 벡터의 곱셈과 결과가 같다. = 기하학적으로 본다면 하나의 벡터를 다른 벡터에 투영(projection)하고 투영된 벡터의 길이와 다른 벡터의 길이를 곱하는 것이다.
-
[ ]
(1x2)행렬과 2d 벡터의 곱셈이란, 2차원 평면 을 1차원 선[ ] 으로 축소(투영, projection)시킨다는 의미를 갖고 있다.
-
를 과 으로 projection시키면 (c, d)가 되는데, [ ] 는 [ ]로 표현할 수 있으며 단위 벡터의 스칼라 값은 그대로 스칼라배 되기 때문에,를 [ ] 으로 projection 시킨다는 것 즉, [ ] 는 가 되는 것이다.
-
내적 곱 (*)
- < 0 : 두 벡터의 방향이 반대,
- = 0 : 두 벡터는 직교
- > 0 : 두 벡터 방향 같음
-
-
이중성(duality, 쌍대성)
-
와 를 2차원 형태의 수선(number line)의 단위 벡터인 에 투영시킨다고 할 때, 대칭성에 의해 에서 수선으로 투영된 위치는 의 x 좌표값이 된다. 마찬가지로 에서 수선으로 투영된 위치는 의 y 좌표값이 된다.
-
즉, 투영변환을 나타내는 1X2 행렬은 의 좌표가 되는 것이다.
-
어떤 공간을 수선(number line)으로 선형변환을 하는 것은, 그 특정 벡터의 내적을 구하는 것과 같다는 것이다.
-
10 & 11. Cross products
-
외적(Cross product)
-
두 벡터의 평행사변형 면적이자, 3차원에서는 평행사변형에 직각인 외적의 벡터의 길이를 의미.
결과값은 단순한 숫자가 아닌, 벡터를 의미. X = -
= , = 일때, 외적은 행렬식인 = -5 이다.
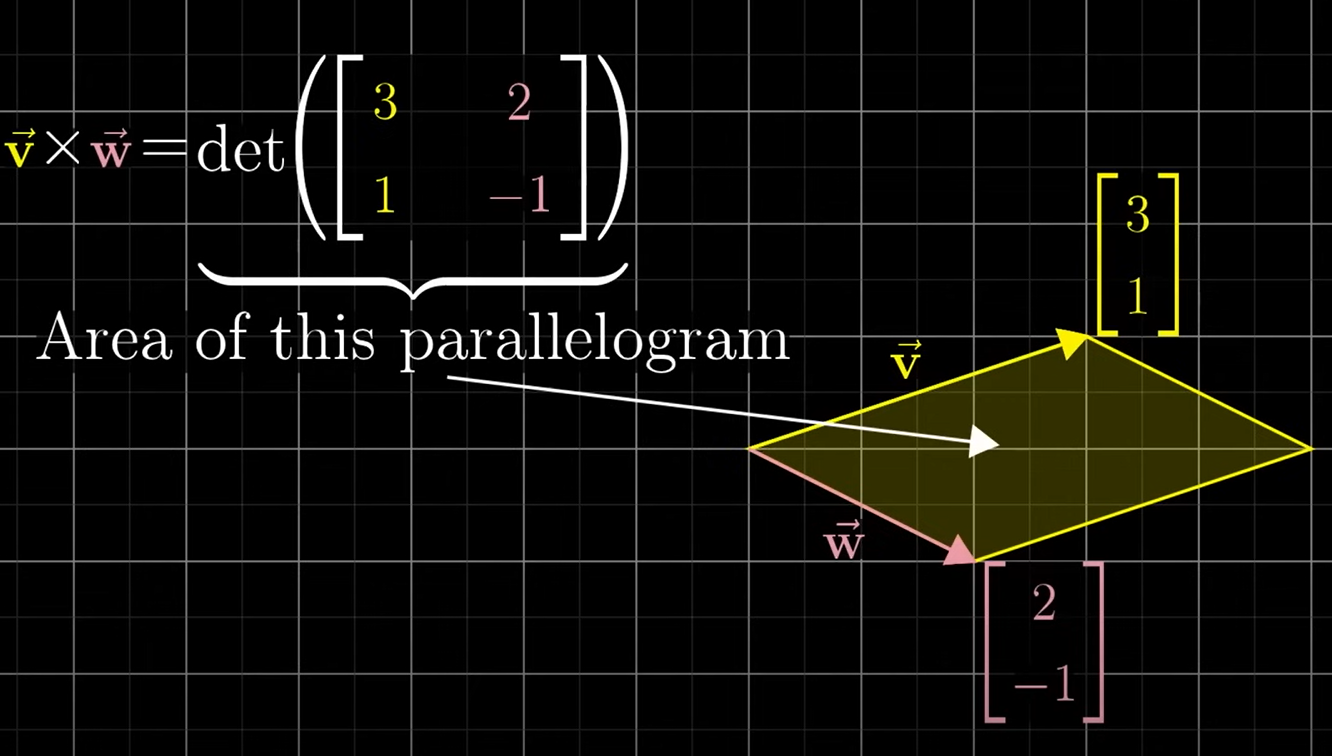
-
가 의 오른쪽에 있으면 양수, 왼쪽에 있으면 음수
-
두 벡터가 수직에 가까울수록 값은 커진다.
-
12. Cramer's rule, explained geometrically
- 내적이 선형변환 이후에도 보존되는 변환은 직교변환이라고 한다.
모든 와 에 대하여 ()*() = * 라면, 는 직교변환(Orthonormal transformations) 이다.
기저벡터의 수직 상태, 길이까지 유지되는 변환이다.- 이를 회전변환행렬(rotation matrices)로 생각할 수도 있다. 고정된 움직임에 대응하는, 늘거나 줄거나 등의 변형이 없는 변환.
-
대부분은 직교변환하지 않는다. 그러므로 선형변환 후에도 입력 벡터에서 변하지 않고 남아 있는 다른 기하학적인 무언가를 찾아본다면 ?
-
= 의 의미는,
를 (a, b)로, 를 (c, d)로 선형변환할 때, (e, f)로 변형되는 (x, y) 를 구하라는 것이다. -
과 (x, y) 벡터의 넓이 = 1 *
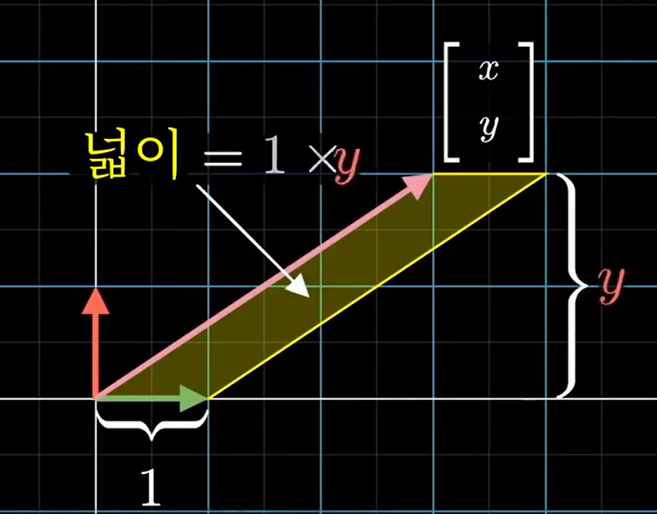
-
선형변환된 이후의 넓이는 만큼 scale 된다.
그러므로, = *
즉, = / 이다.
'' 는 로 표현할 수 있으므로, -
= /
-
마찬가지로, = /
13. Change of basis
-
J의 기저벡터가 = , = 라고 할 때. J입장에서 = 는 우리 입장 (, ) 에서 어떻게 표현할 수 있을까 ?
-
[J 기저벡터] [J언어] = [우리언어]
=즉, J 관점의 는 우리 관점에서 이다.
-
-
[J 기저벡터] [J언어] = [우리언어]
[J언어] = [J 기저벡터] [우리언어]
-
아래 행렬곱은 무엇을 의미할까?
J 의 기저벡터 = =
새로운 선형변환 = = 90도 회전
J 입장
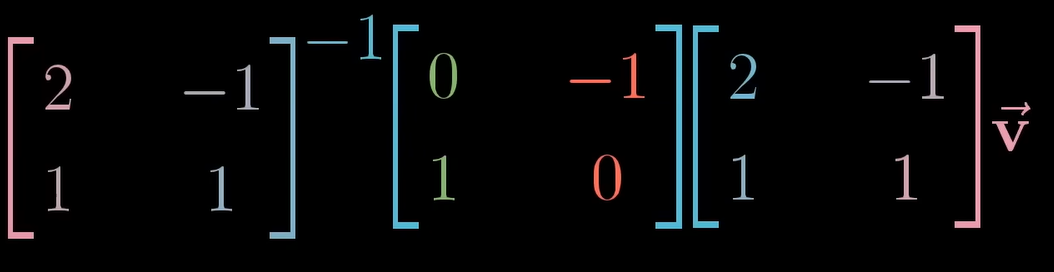
= J입장 벡터()를 우리 입장에서 새로운 선형변환을 취해 J의 언어로 표현한 것.
= J입장 벡터()를 우리 입장(J 기저벡터를 곱하여)에서 새로운 선형변환(새로운 선형변환 곱)을 취해 J의 언어로 표현(J기저벡터의 역행렬)한 것.
= [J 기저벡터] [새로운 선형변환] [J 기저벡터] [J입장 ]
= [J 기저벡터] [새로운 선형변환] [우리 입장 ]
= [J 기저벡터] [우리 입장 새로운 선형변환]
= [J 입장 새로운 선형변환된 벡터]
=> : 선형변환
=> : 관점의 변환
14 & 15. Eigenvectors and eigenvalues
-
고유벡터(Eigenvectors) : 선형변환 후 벡터가 선형변환 전 벡터의 스팬에 포함되어 있는 경우. 즉, 선형변환을 해도 스케일링만 변하고 자신의 span을 벗어나지 않는 벡터
-
고윳값(Eigenvalues) : 고유벡터가 변환될 때 상수배되는 값
-
특징
- 모든 선형변환에 고유벡터가 있는 것은 아님.
- 고윳값은 하나여도 여러개의 고유벡터를 가질 수 있ㄷ음.
-
아래 그림은, 행렬-벡터 곱셈()가 고유벡터()를 임의의 상수(, 고윳값)로 스케일링한 결과와 같다는 것.
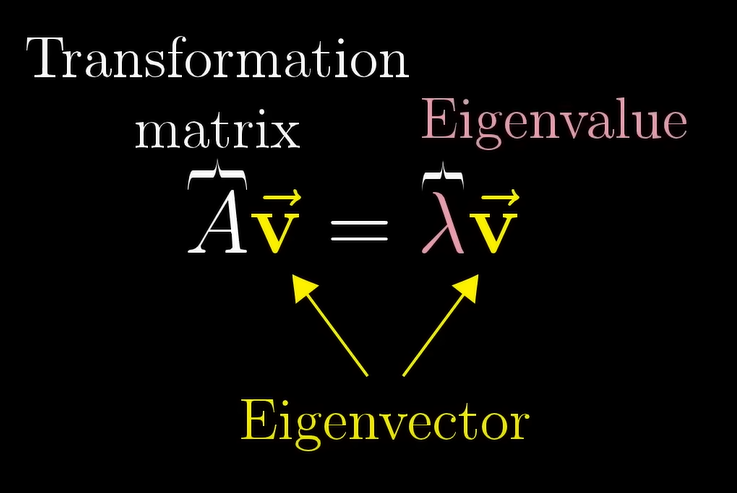
=
- = 0
= 0 ( 는 로 쓸 수 있음.)
-> 두 행렬곱의 선형변환이 영벡터가 된다는 것. 이때, 영벡터가 아닌 고유벡터 를 찾고 있기 때문에, = 0인 값을 찾아야 함. -
고유기저(Eigenbasis) : 기저벡터(, )가 고유벡터일 경우, (고유벡터의 행렬)은 대각선 외에 모두 0인 대각선 행렬(diagonal matrix)가 된다.
-
대각선 행렬(diagonal matrix) : 모든 기저벡터는 고유벡터이고, 대각선의 값들이 고유값이 됨
-
선형변환에서 고유벡터유벡터가 많다면, 이 고유벡터들을 기저벡터로 사용할 수 있다.
-
의 고윳값() 계산식
- 특징 1)
-> 고윳값의 평균 () = - 특징 2)
-> 고윳값의 곱 () = - ||와 사이의 거리가 라고 했을 때,
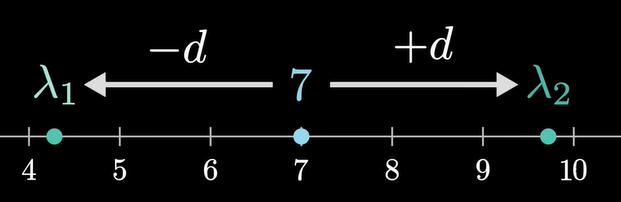
=
= - p
- 특징 1)
-
의 고윳값은 ?
16. Abstract vector spaces
-
선형 변환은 합과 실수배를 보존한다.
- 합(additivity) :
- 실수배(scaling) :
-
미분 역시 선형변환이다.
-
선형대수에서 사용되는 컨셉은 (<->) 함수에서도 사용되는데,
- Linear transformations <-> Linear operators
Dot products <-> Inner products
Eigenvectors <-> Eigenfunctions
- Linear transformations <-> Linear operators
-

