Consistent Hashing (안정 해시) 설계
본 내용은 "가상 면접으로 배우는 대규모 시스템 설계" 책의 5장의 주제인 "안정 해시 설계"에 대한 내용을 정리하고 추가적인 자료조사로 내용의 이해를 높이기 위해 작성됐습니다.
본론에 앞서기 전에 "안정 해시"는 특정 문제를 해결하기 위한 기술입니다. 그래서 어떤 문제들을 해결할 수 있는 개념인지 이해하고 접근하는 것이 중요할 것 같습니다.
문제: 균등하게 분배해야한다.
일반적으로 특정 서비스의 규모가 커질 때 즉, 트래픽이 증가하면서 정상적인 서비스 운영을 하기 위해 수평 확장(horizontal scaling)을 필요로 합니다.
이러한 수평 확장의 필수는 "얼마나 규모를 늘려야 적당할까?" 라는 대략적 규모의 추정이 중요하게 됩니다. 하지만 아무리 예상을 하더라도 특정 시간, 사건에 의해 몰리는 트래픽을 예상하는 것은 불가능하고 너무 많이 서버를 증설하게 되면 굉장히 비효율적인 설계가 되어 비용이 낭비되게 됩니다. 이러한 문제를 해결하기 위해서는 가용성을 잃지 않고 트래픽의 양에 따른 동적으로 서버의 양을 조절하고 각 서버에 균등하게 트래픽이 분배되도록하는 것이 중요합니다. 맞습니다. 이 문제를 안정 해시가 해결해줍니다.
해시 키 재분배(Rehash) 문제
균등 분배를 해야한다고 요구사항이 생길 때 가장 나이브한 접근방법으로 서버 대수를 이용한 나머지 연산(모듈러 연산)으로 트래픽을 보낼 서버를 결정하는 방법입니다.
serverIndex = hash(key) % N
* N: count of server위 문제는 서버의 수가 항상 고정되어 있다고 가정하면 무리없이 동작할 것으로 보입니다. 하지만, 서버 장애는 거의 필수적으로 발생한다고 생각하는 편이 좋은 설계를 이끌도록 만들어주니 하나의 서버가 다운되는 상황을 상상해봅시다.
위 내용처럼 고정된 해시함수(hash)를 사용할 경우, N -> N-1으로 서버의 수가 줄어들 경우, 특정 서버에 캐시로 빠른 결과를 얻고 있던 사용자들의 트래픽들이 다시 캐시가 없는 다른 서버로 요청을 하게 됩니다.
이 과정에서 발생하는 해시키 재분배는 굉장히 큰 비용을 요구하게 됩니다. "대규모 Cache Missing이 발생한다"라고 책에서는 묘사되어있습니다.
위는 서버한대가 장애로 하나로 줄어드는 경우를 예로 들었지만 급변하는 트래픽에 가용서버의 수를 늘릴 경우를 상상해봅시다. 점진적으로 늘어날때마다 계속 대규모 해시키 재분배를 발생시킬테고 사용자들의 경험이 중요한 이벤트 서비스에서 이러한 상황이 발생할 경우를 상상해봅시다. 충분히 해결하는데 시간을 많이 들일 필요가 있습니다.
안정 해시 Consistent Hashing
위키피디아에서 정확한 정의를 먼저 살펴보겠습니다.
In computer science, consistent hashing is a special kind of hashing technique such that when a hash table is resized, only n/m keys need to be remapped on average where n is the number of keys and m is the number of slots.Hash Table의 사이즈가 변화할때 오직 평균적으로 n/m 개의 키만 재배치할 수 있도록하는 특별한 해싱 기술이라고 설명합니다.
앞서 설명했던 고정 해시함수를 이용했던 방식과의 차이는 재배치해야하는 해시키의 수를 "오직 평균적으로 n/m 개의 키만"으로 줄이는 방법이 무엇인지 집중해볼 필요가 있습니다.
해시링 위에 해시 값과 서버 도식화
책에서는 "해시 공간"과 "해시 링"으로 이 알고리즘에 대한 원리를 설명합니다. 해시 공간을 원으로 이어서 표현하는 방식 굉장히 알고리즘에 대한 가독성을 높여주는 것 같습니다.
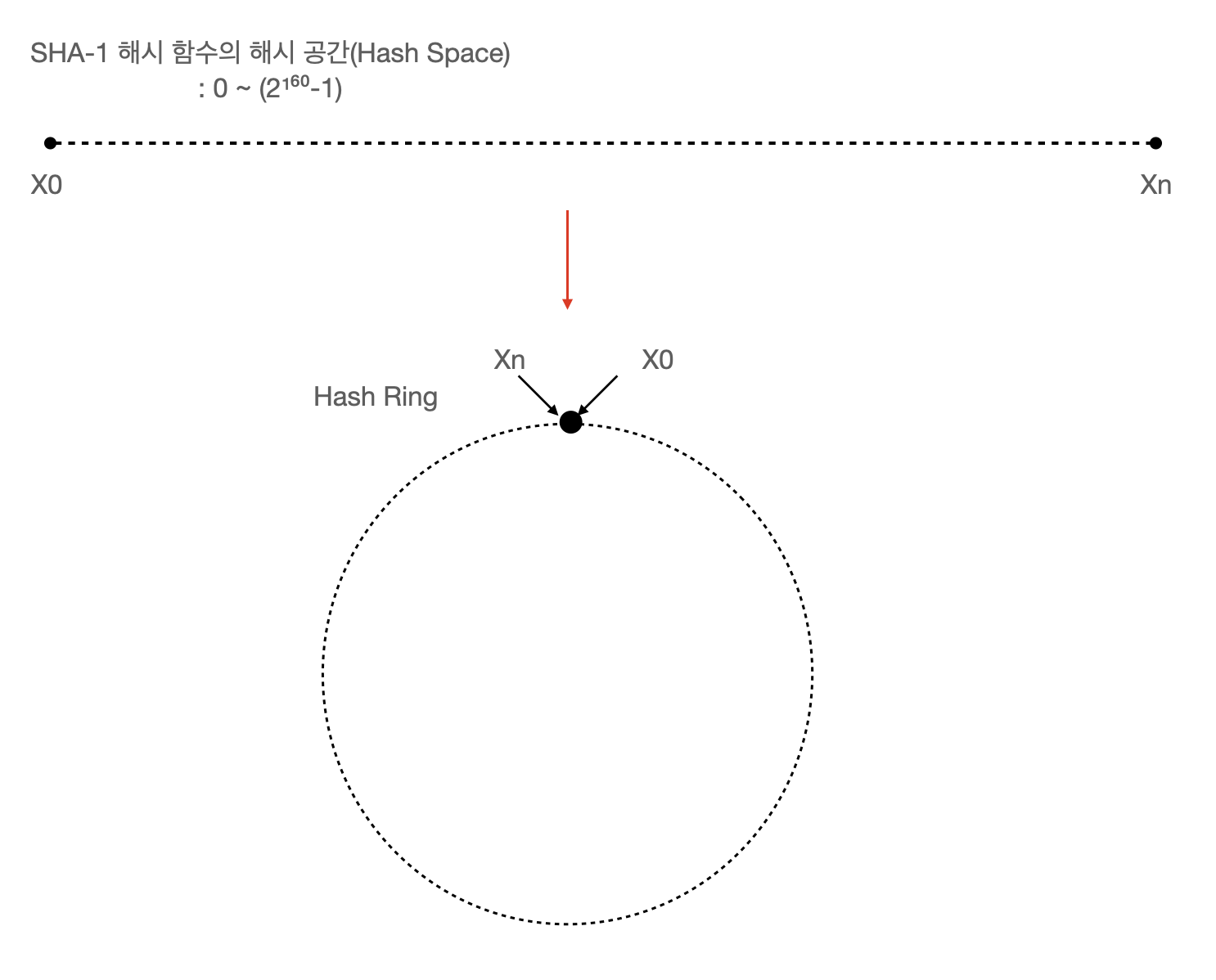
해시 링위의 있는 dot(점)은 SHA-1 해시 함수에 의해 계산되어 나온 결과 값이 전체 해시 결과 범위에서 어디 쯤 위치하는지를 나타내게 됩니다. 이러한 묘사 방식은 해시서버를 해시링 위에 같이 배치하여서 어떤 값들이 어떤 서버로 향하게 되는 쉽게 이해할 수 있도록 도와줍니다.
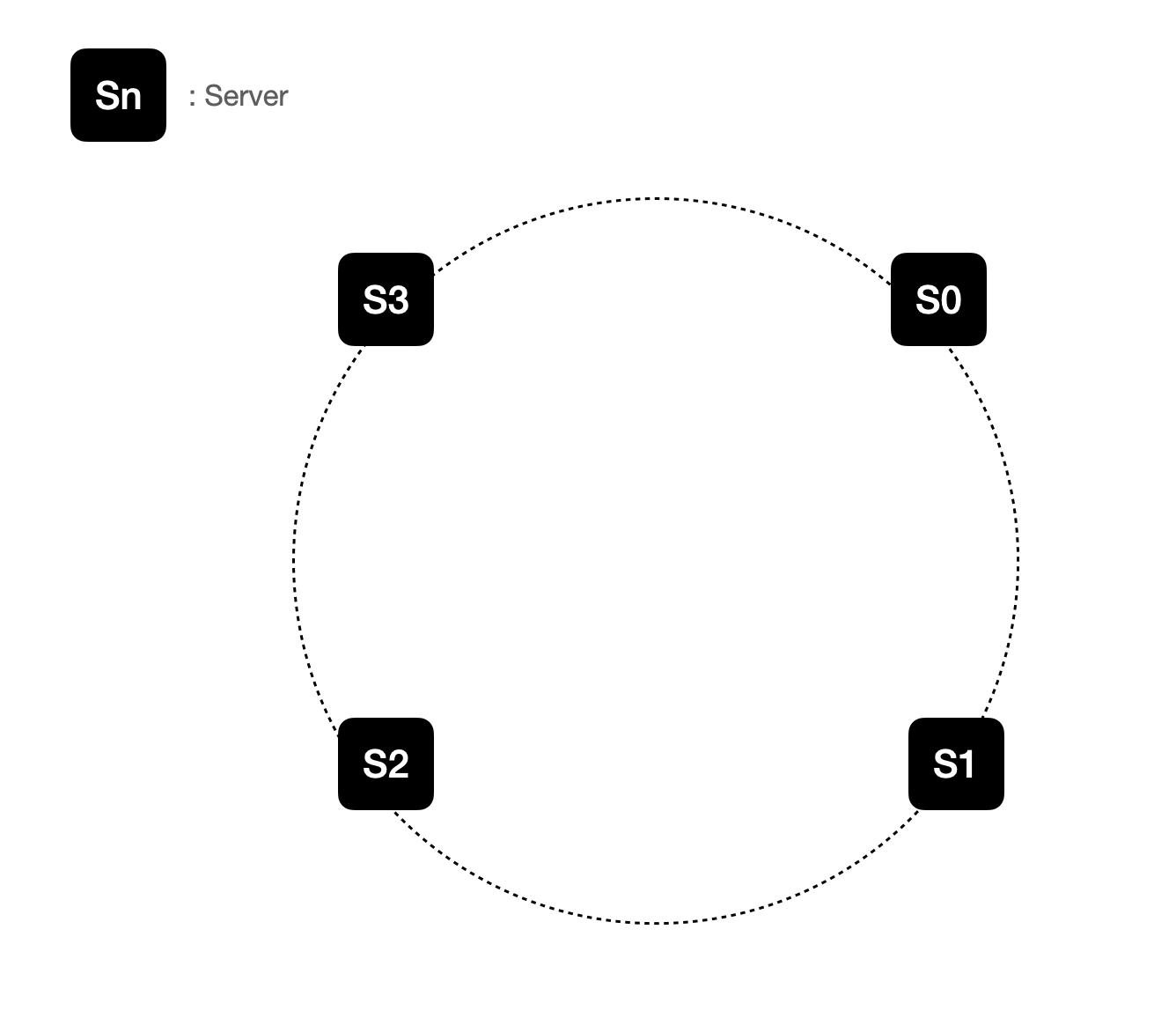
각 서버를 위와 같이 해시링 위에 동일한 간격으로 배치합니다.
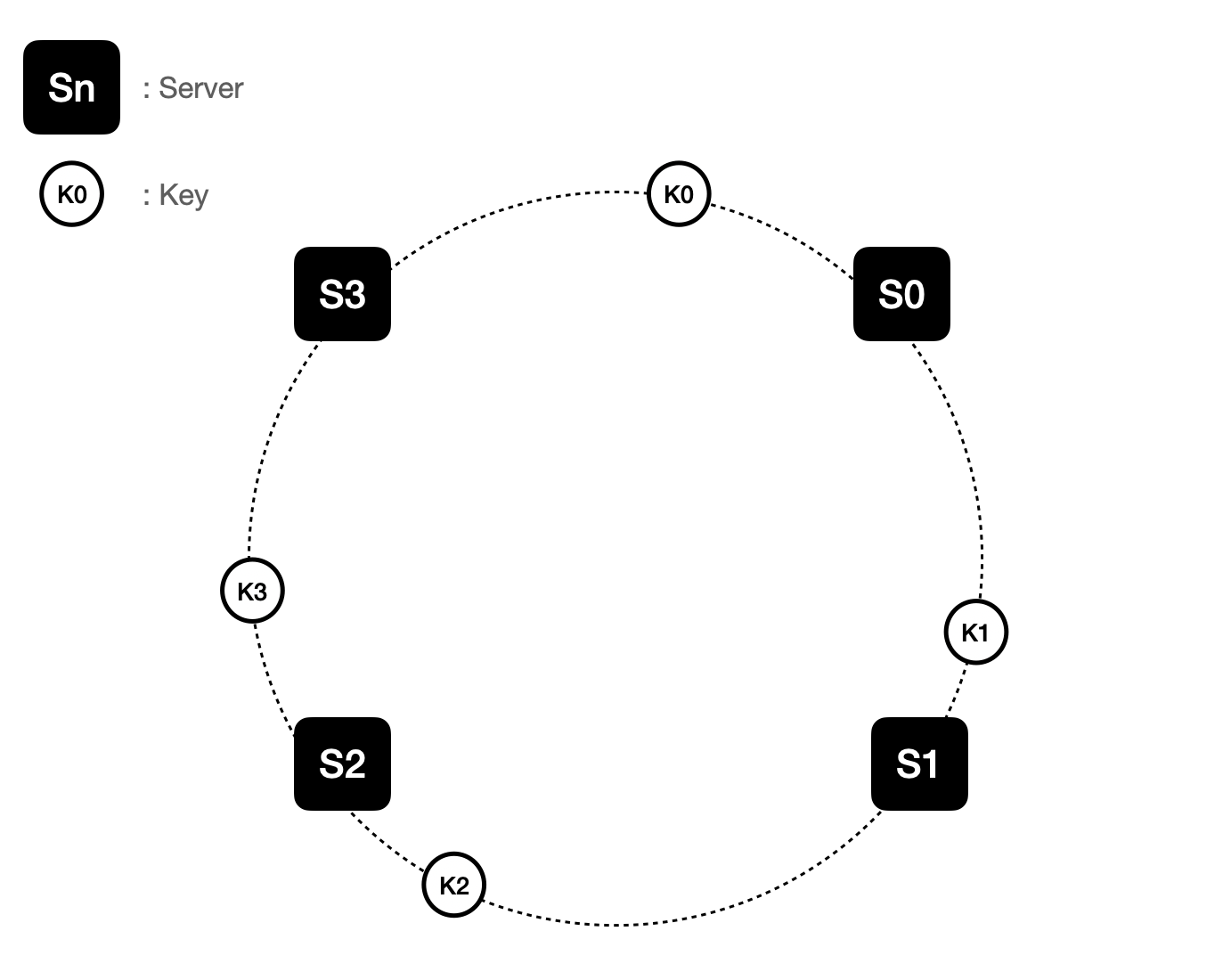
그리고 각 키 값들이 해시함수에 의해 어디에 배치되는지를 나타냅니다.
서버 조회 방식
안정 해시에서 특정 키가 어떤 서버로 접속해야하는지에 대한 기준은 해시링위에서의 시계 방향으로 링을 탐색해나가면서 만나는 첫 번째 서버 접속해야 서버입니다.
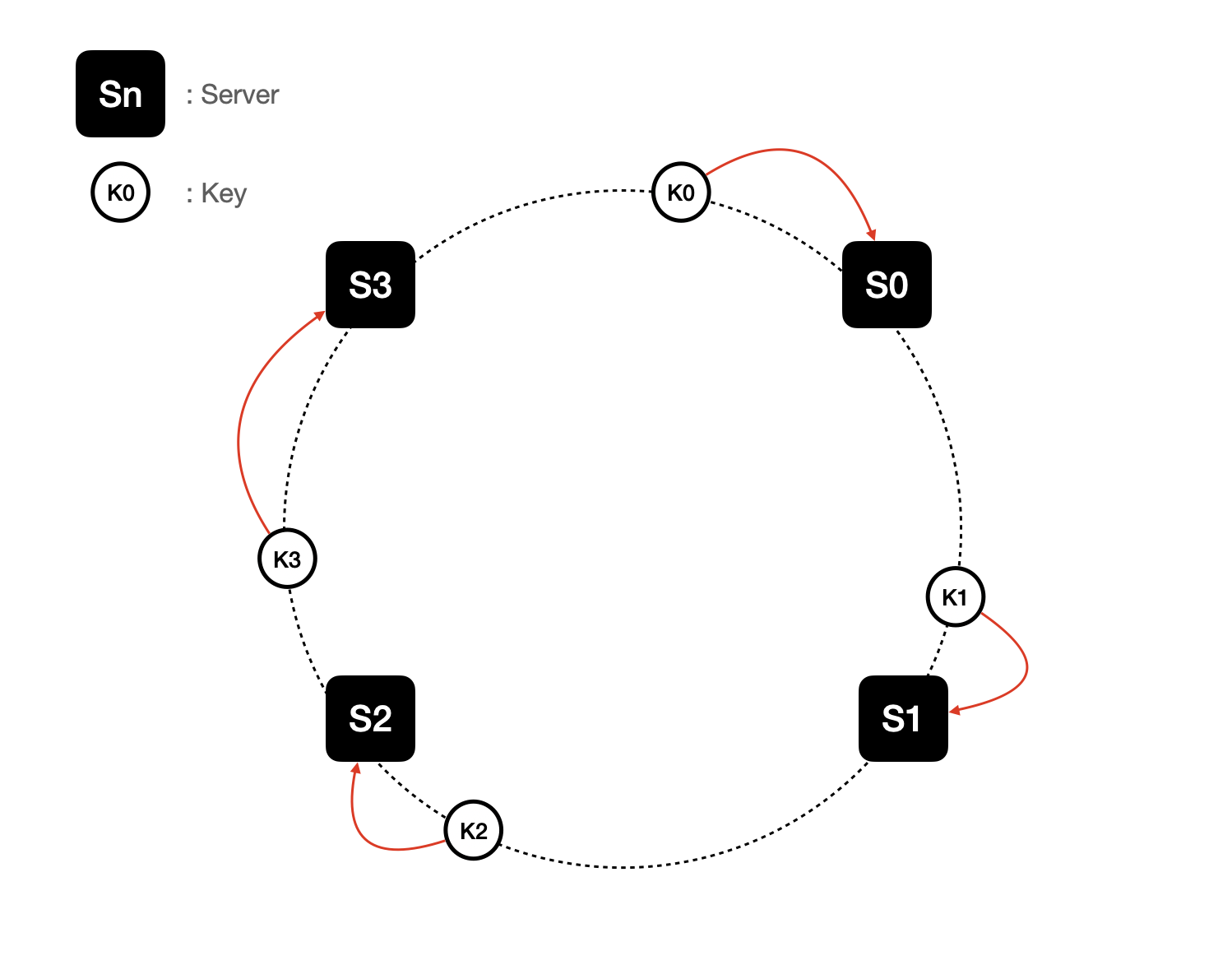
새로운 서버 추가에 의한 해시 재배치
이러한 방식으로 접속해야할 서버를 찾는 방식을 따른다면 서버를 추가하더라도 키 가운데 일부만 재배치하면 되기 때문에 대규모 해시 재배치가 일어나지 않습니다.
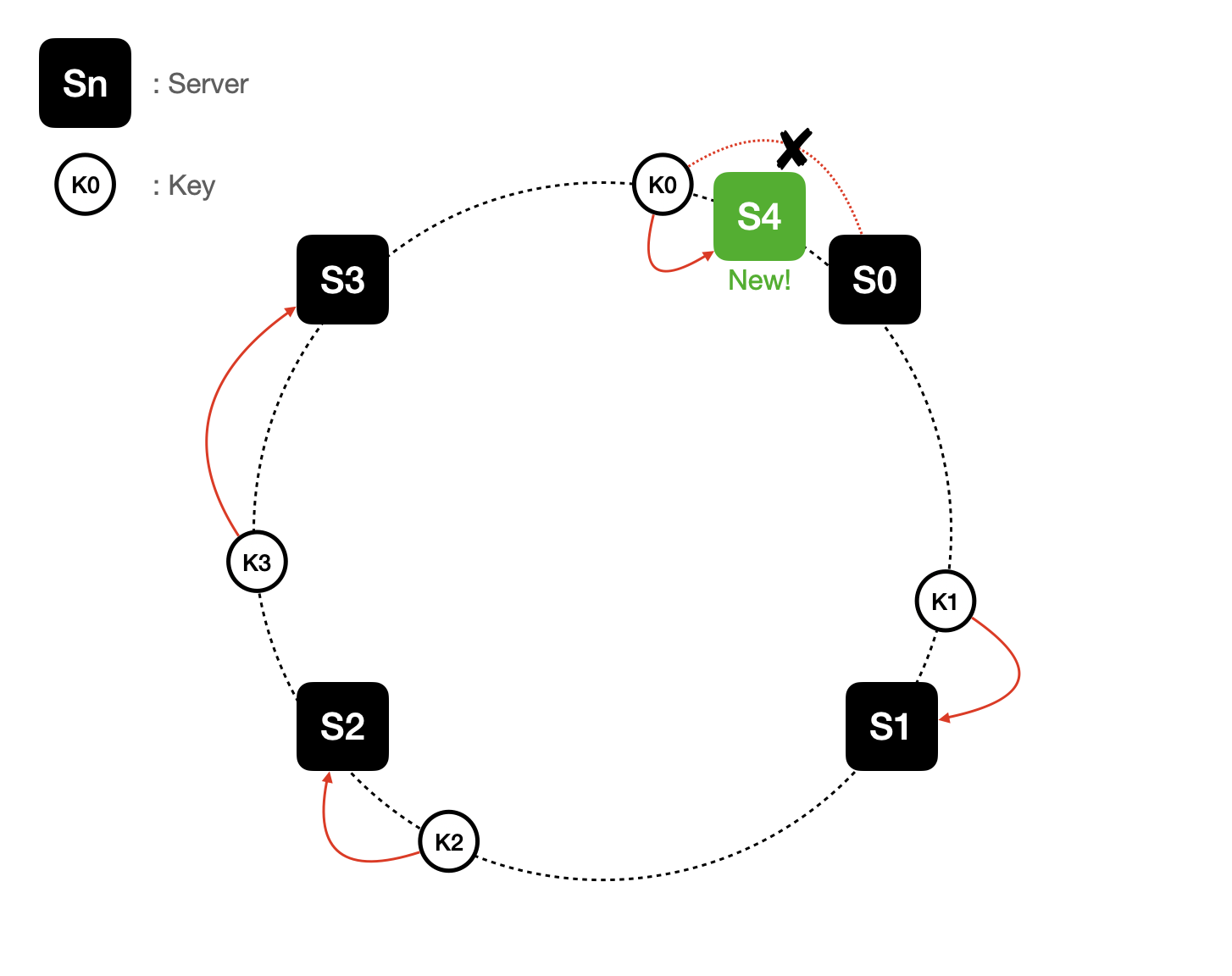
서버 제거에 의한 해시 재배치
마찬가지로 서버가 제거되더라도 S0 ~ S1 사이의 키들만 S2 로 해시 재배치가 발생하게 됩니다.
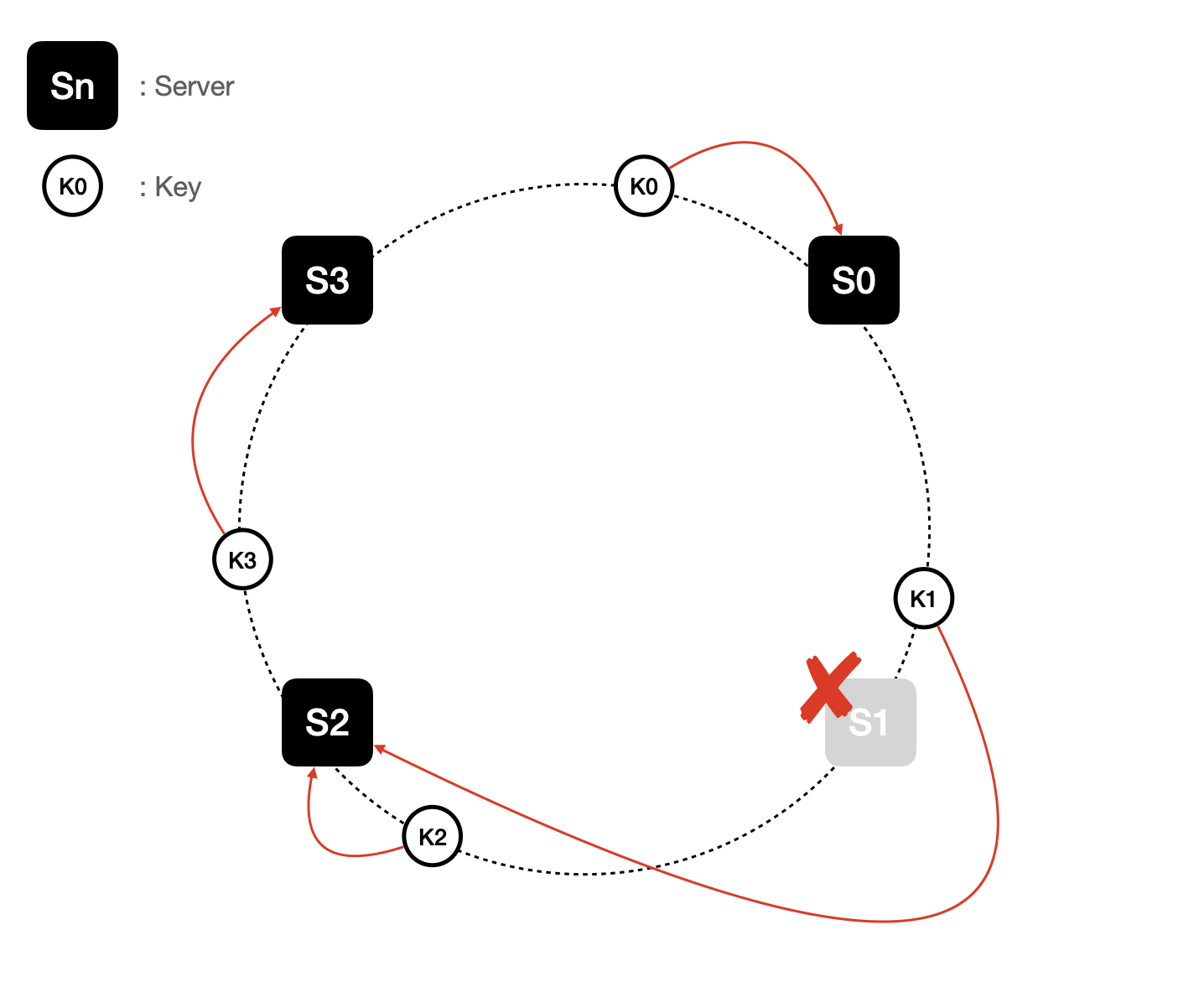
여기까지가 안정해시에 대한 기본 구현법입니다.
기본 구현법에서 두 가지 문제
기본 구현법을 간단히 정리해보면 아래와 같습니다.
- 서버와 키를 균등 분포(uniform distribution) 해시 함수를 사용해 해시 링에 배치한다.
- 키의 위치에 링을 시계 방향으로 탐색하다 만나는 최초의 서버가 키가 저장될 서버다.
하지만 이 접근법에는 두가지 문제가 있습니다. 서버가 지속적으로 추가되거나 삭제되다보면 인접 서버사이의 해시 공간(파티션, partition)를 균등하게 유지하는게 불가능하다는 것입니다.
어떤 서버는 너무 작은 해시 공간을 할당받고 어떤 서버는 너무 큰 해시 공간을 할당받는 상황이 가능하다는 것입니다. 균등하게 분배해야한다는 목적과 멀어지게됩니다.
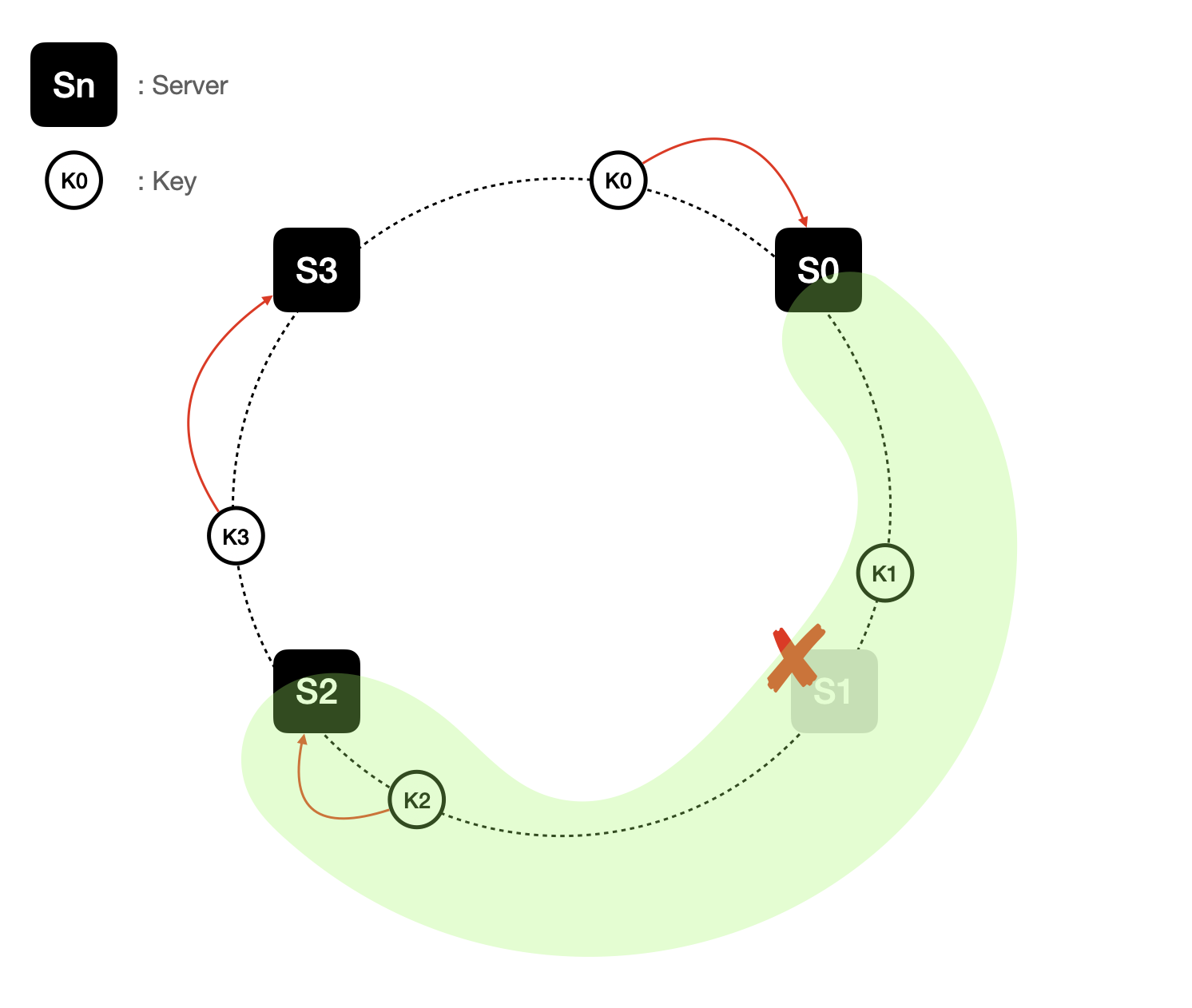
균등 파티션을 위한 해결책: Virtual Node(가상 노드)
가상 노드는 실제 노드 또는 서버를 가리키는 노드로서, 하나의 서버는 링 위에 여러 개의 가상 노드를 가질 수 있습니다.
아래와 같이 서버 0과 서버 1은 3개의 가상 노드를 갖게 됩니다. 여기서 가상 노드의 수는 임의로 지정한 것이며, 실제 서버에서는 파티션 균등성을 위해 훨씬 큰 값을 사용합니다.
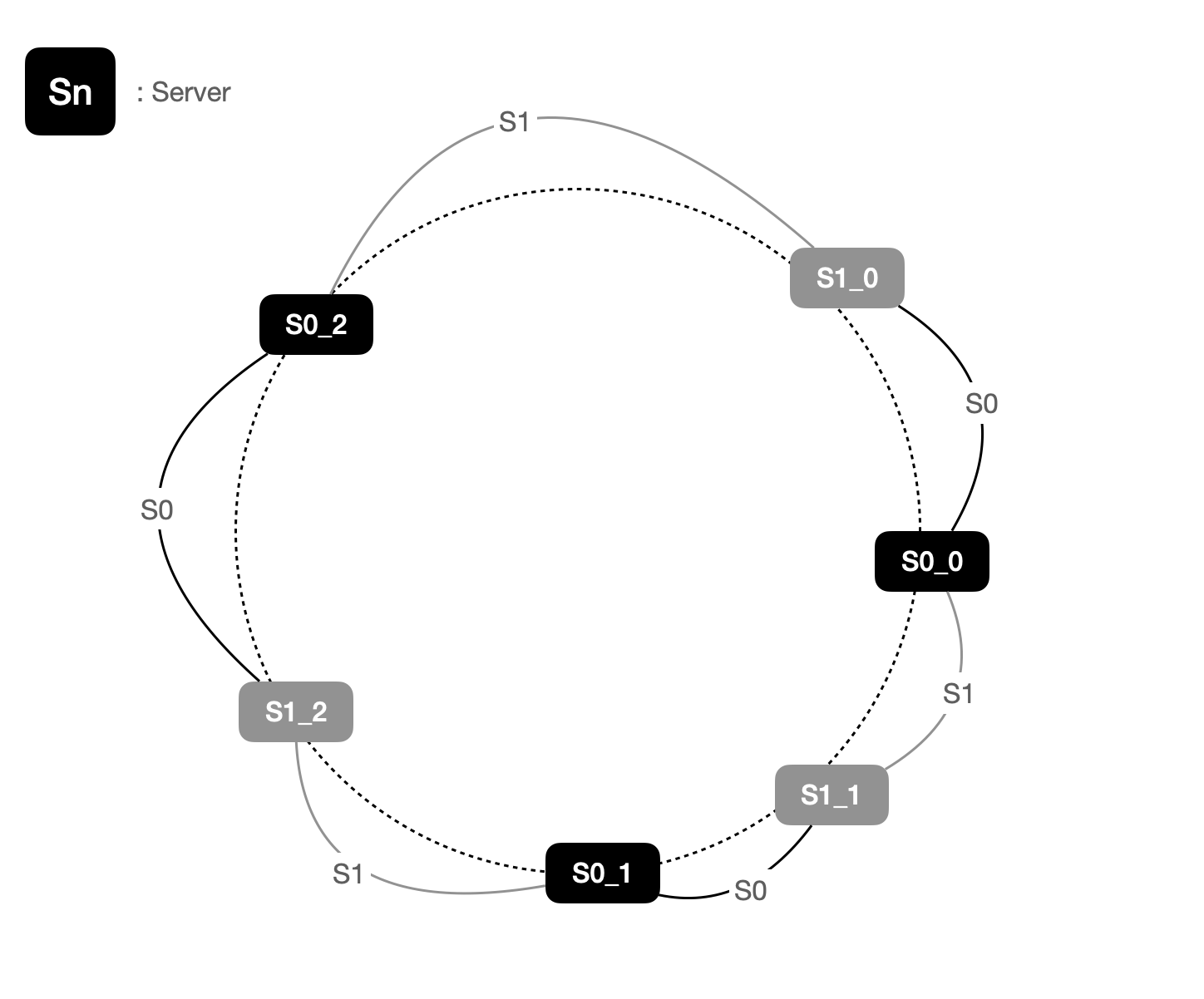
마찬가지로 키의 위치로부터 시계방향으로 링을 탐색하다가 만나는 최초의 가상 노드가 해당 키가 저장될 서버가 됩니다.
가상 노드의 개수를 늘리면 키의 분포는 점점 균등해집니다. 표준편차(standard-deviation)가 작아져서 데이터가 고르게 분포되기 때문입니다.
100~200개의 가상 노드를 사용했을 경우 표준편차의 값은 평균 5%(가상 노드가 200개인 경우)에서 10%(가상노드가 100개인 경우)사이가 됩니다.
가상 노드의 개수가 늘어날 수록 표준편차의 값은 더 떨어지게 됩니다. 그러나 가상 노드 데이터를 저장할 공간은 더많이 필요하게 됩니다. 시스템 요구사항에 따라 적절한 trade-off가 필요합니다.
안정 해시 정렬에 대한 구현체
마지막으로 위에서 설명한 이론적인 내용에서 빈공간으 구현체를 보면서 채워가도록 합시다.
import java.util.Collection;
import java.util.SortedMap;
import java.util.TreeMap;
public class ConsistentHash<T> {
private final HashFunction hashFunction;
private final int numberOfReplicas;
private final SortedMap<Integer, T> circle =
new TreeMap<Integer, T>();
public ConsistentHash(HashFunction hashFunction,
int numberOfReplicas, Collection<T> nodes) {
this.hashFunction = hashFunction;
this.numberOfReplicas = numberOfReplicas;
for (T node : nodes) {
add(node);
}
}
public void add(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.put(hashFunction.hash(node.toString() + i),
node);
}
}
public void remove(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.remove(hashFunction.hash(node.toString() + i));
}
}
public T get(Object key) {
if (circle.isEmpty()) {
return null;
}
int hash = hashFunction.hash(key);
if (!circle.containsKey(hash)) {
SortedMap<Integer, T> tailMap =
circle.tailMap(hash);
hash = tailMap.isEmpty() ?
circle.firstKey() : tailMap.firstKey();
}
return circle.get(hash);
}
}책의 내용을 읽고 저는 새로 추가되는 서버 노드들은 Hash Ring의 어디에 배치하는지 그 기준이 궁금했었습니다.
The location of each replica is chosen by hashing the node's name along with a numerical suffix, and the node is stored at each of these points in the map.
해시함수가 균등하게 분포된다는 가정이 있어서 간단히 노드이름 + numerical suffix를 해시함수 연산을 통해 위치를 결정함을 확인할 수 있었습니다. 이렇게 하면 균등 분배가 되어 공평한(?) 위치로 선정이 되나 궁금함이 또 생겨서 검색해보니 좋은 Hash Function은 Uniformity 성질이 있기 때문에 그 부분은 해시함수의 역할임을 알 수 있었습니다. 나중에 시간이 생기면 해시함수를 선택하는 기준도 따로 학습해볼 가치가 있을 것 같습니다.
마무리
"균등한 분배"를 위해 실제로 널리 사용되는 안정 해시 기술에 대해 알아보았습니다.
이러한 기술은 웹서비스 개발에 자주 사용하는 아래와 같은 서비스에서 활용하고 있다고 합니다.
- 아마존 다이나모 데이터베이스(Dynammo DB)의 파티셔닝 관련 컴포넌트
- 아파치 카산드라(Apache Cassandra) 클러스터에서의 데이터 파티셔닝
- 디스코드(Discord) 채팅 어플리케이션
- 아카마이(Akamai) CDN
- 매그래프(Meglev) 네트워크 부하 분산기
그리고 로드벨런싱에 흔히 사용되는 NGINX에서도 안정해시 알고리즘을 지원하고 있습니다.
https://www.nginx.com/faq/what-are-the-load-balancing-algorithms-supported/
- Round Robin and weighted Round Robin
- Least Connections and weighted Least Connections
- Least Time and weighted Least Time
- IP Hash (based on client IP address) and weighted IP Hash
- Hash (on specified request characteristics)
- Consistent (ketama) Hash <---- here!
- Random with Two Choices안정 해시 기법 이외에도 분배 방식에 대한 방법론이 많네요.
만약에 트래픽을 고려한 설계를 할 수 있는 포지션(devops)라면 시간을 내서라도 각 알고리즘의 장단점을 알아야될 것 같습니다! 하지만 토끼굴에 빠지지않기 위해서 이에 대한 내용은 다음으로 미루도록 하겠습니다.
