⌚ 활동 시간 : 2023년 1월 28일 오후 8시 ~ 오후 11시
✨ 목표 : 모두의 딥러닝 10 ~ 12장 내용을 공부하고 정리하였다.
본격적으로 딥러닝 모델 코드를 작성하는 방법을 공부했다. 책에 나온 예제와 설명을 통해 함수 하나하나를 이해할 수 있어서 좋았다.
🎈 10장
딥러닝 모델 설계 예제를 설명한다.
폐암 수술 환자의 생존률을 예측하는 모델을 예로 설명한다.
이 책에서는 tensorflow의 keras를 사용한다.
예제 코드의 전체적인 과정은 다음과 같다.
- Sequential()을 통해 model함수 선언
- model에 은닉층, 출력층 추가하기
- 설계한 model을 컴파일하기
- fit()으로 학습 수행하기
사용되는 함수 설명
Sequential()
: 층을 선형으로 연결한다.
: 각 레이어에 정확히 하나의 입력 텐서와 하나의 출력 텐서가 있는 일반 레이어 스택에 적합하다.
: 모델 또는 레이어에 다중 입력, 다중 출력이 있으면 적합하지 않다.
from tensorflow.keras.models import Sequential
model = Sequential([Dense(...), Activation(), ...])
add()
: 모델에 새로운 층을 추가한다.
model.add(...)
Dense()
: 첫번째 인자 - 몇 개의 노드를 해당 층에 만들 것인지 전달한다.
: input_dim - 입력의 형태 지정, 입력 데이터에서 몇개의 값을 가져올지 정한다.
: activation - 활성화 함수를 정한다.
: 출력층일 경우 첫번째 인자 값을 1로 한다.
model.add(Dense(10, input_dim = 10, activation = 'relu'))
compile()
: loss - 손실함수를 정한다.
: 손실함수는 최적의 가중치를 정하기 위해 필요하다. Keras에서는 선형 회귀 모델에서 사용되는 평균 제곱 계열의 손실함수와 교차 엔트로피 계열 손실함수를 제공한다.
: optimier - 옵티마이저를 정한다.
: metrics - 모델의 수행 결과를 보여준다. (accuracy, loss, val_acc...)
model.compile(loss=..., optimizer=..., metrics = ['...'])
fit()
: epochs - 모든 샘플이 한 번 실행되는 횟수이다.
: batch_size - 한 번에 처리하는 샘플의 개수이다.
: batch_size가 너무 작으면 실행 편차가 생기고, 너무 크면 학습 속도가 느려진다. 따라서 적절한 batch_size를 정하는 것이 중요하다.
model.fit(X, y, epochs=..., batch_size=...)
🎈 11장
주어진 데이터의 분포 및 형태를 확인하는 방법을 설명한다.
피마 인디언 데이터를 예제로 설명한다.
가장 효과적으로 데이터를 파악하는 방법은 데이터를 시각화 하는 것이다. pandas라이브러리의 함수를 사용하면 데이터의 분포를 쉽게 확인할 수 있다.
사용되는 함수 설명
value_counts()
: 한 칼럼이 갖는 값의 개수를 계산한다.
describe()
: 각 칼럼별 샘플 수, 평균, 표준편차, 최솟값, 백분위 수 25%, 50%., 75%에 해당하는 값, 최대값을 계산한다.
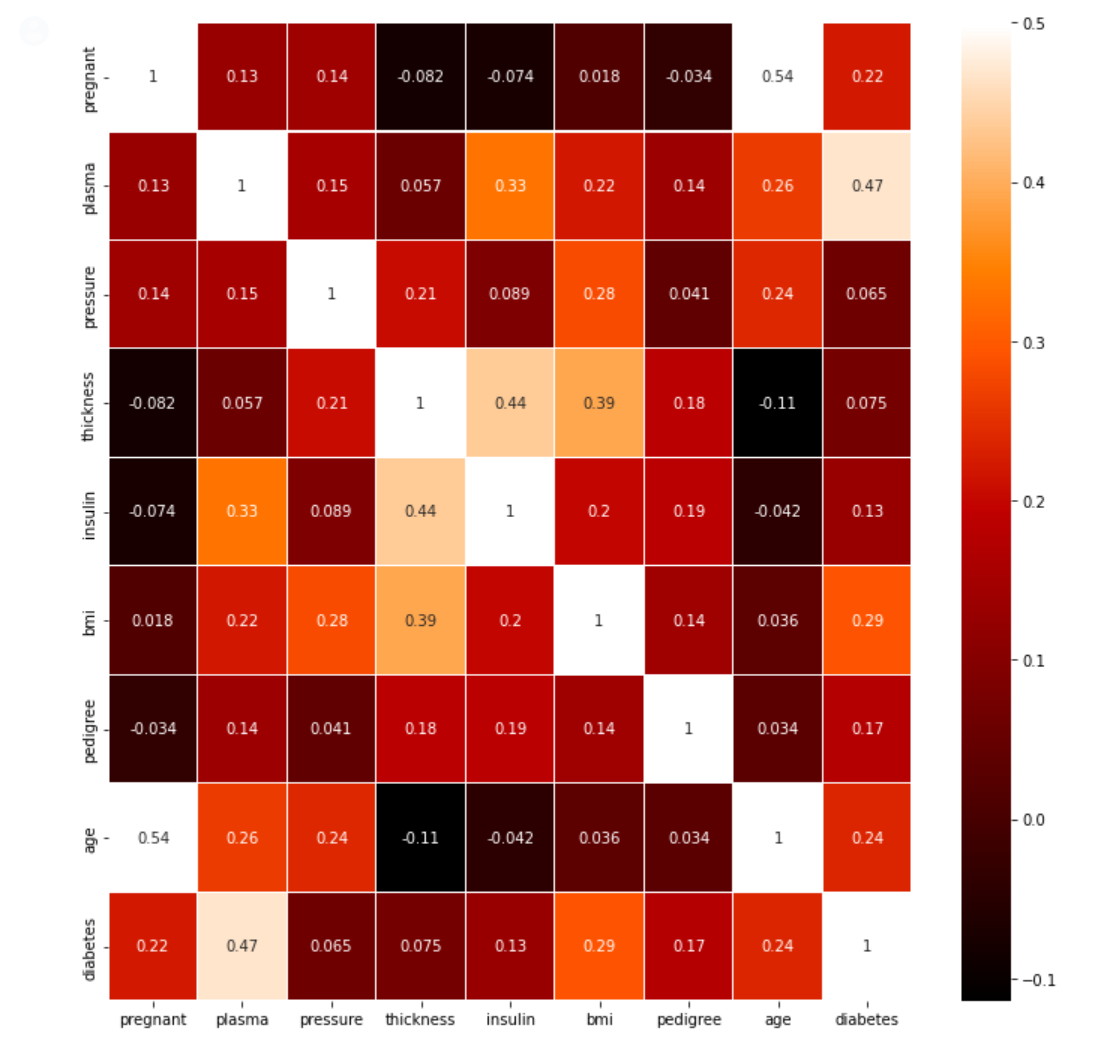
corr()
: 각 칼럼이 서로 다른 칼럼과 상관되는 정도를 계산한다.
model.summary()
: Layer - layer의 이름을 나타낸다.
: Output Shape - 한 layer에서 몇 개의 출력이 발생하는지를 나타낸다.
: Param - 가중치와 바이어스 수의 합을 나타낸다.

🎈 12장
다중 분류 문제를 해결하는 방법에 대해 설명한다.
아이리스 품종 예측 모델을 예제로 설명한다.
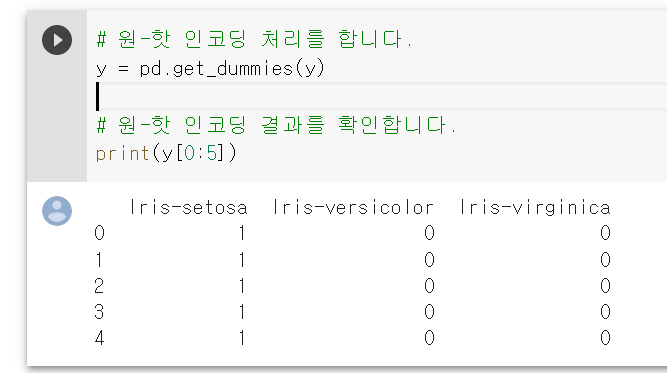
클래스에 해당하는 값이 문자열이라면 이를 0과 1의 값으로 변경해야한다. 이는 one-hot encoding을 통해 해결할 수 있다. pandas에서 제공하는 get_dummies()를 사용하면 one-hot encoding이 적용된다.
ont-hot encoding은 해당하는 단어의 인덱스에 1을 부여하고 다른 인덱스에는 0을 부여하는 단어의 벡터 표현 방식이다.
이번 예제의 경우 2개의 결과 중 하나로 예측하는 것이 아닌, 3가지의 확률을 계산해야하므로 softmax함수가 사용된다. softmax함수는 항목당 예측 확률을 0과 1사이의 값으로 정규화하여 나타낸다. 따라서 모든 예측 확률의 총합은 항상 1이 된다.
이번 예제는 다항 분류 모델이기 때문에 손실함수로 binary_crossentropy가 아닌 categorical_crossentropy를 사용한다.
