이모티콘 (Gold IV)

문제 링크

문제 설명

영선이는 매우 기쁘기 때문에, 효빈이에게 스마일 이모티콘을 S개 보내려고 한다.

영선이는 이미 화면에 이모티콘 1개를 입력했다. 이제, 다음과 같은 3가지 연산만 사용해서 이모티콘을 S개 만들어 보려고 한다.

화면에 있는 이모티콘을 모두 복사해서 클립보드에 저장한다.
클립보드에 있는 모든 이모티콘을 화면에 붙여넣기 한다.
화면에 있는 이모티콘 중 하나를 삭제한다.
모든 연산은 1초가 걸린다. 또, 클립보드에 이모티콘을 복사하면 이전에 클립보드에 있던 내용은 덮어쓰기가 된다. 클립보드가 비어있는 상태에는 붙여넣기를 할 수 없으며, 일부만 클립보드에 복사할 수는 없다. 또한, 클립보드에 있는 이모티콘 중 일부를 삭제할 수 없다. 화면에 이모티콘을 붙여넣기 하면, 클립보드에 있는 이모티콘의 개수가 화면에 추가된다.

영선이가 S개의 이모티콘을 화면에 만드는데 걸리는 시간의 최솟값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 S (2 ≤ S ≤ 1000) 가 주어진다.

출력

첫째 줄에 이모티콘을 S개 만들기 위해 필요한 시간의 최솟값을 출력한다.

문제 풀이

• bfs 좀 할줄아나,, 싶어서 이 문제 푸는데 한참을 봤다
• 복사, 붙여넣기 삭제 까지는 알겠는데
• 세가지 방법으로 최소값 찾는거니까 bfs 인 것도 알겠는데 방문처리가 막막한 것,,,
• 결국 구선생 도움을 받으니 이놈은 또 이중배열로 방문처리를 받더라 그래서 생각해보니까 진짜 그래야 최소값을 찾을 수 있다
  
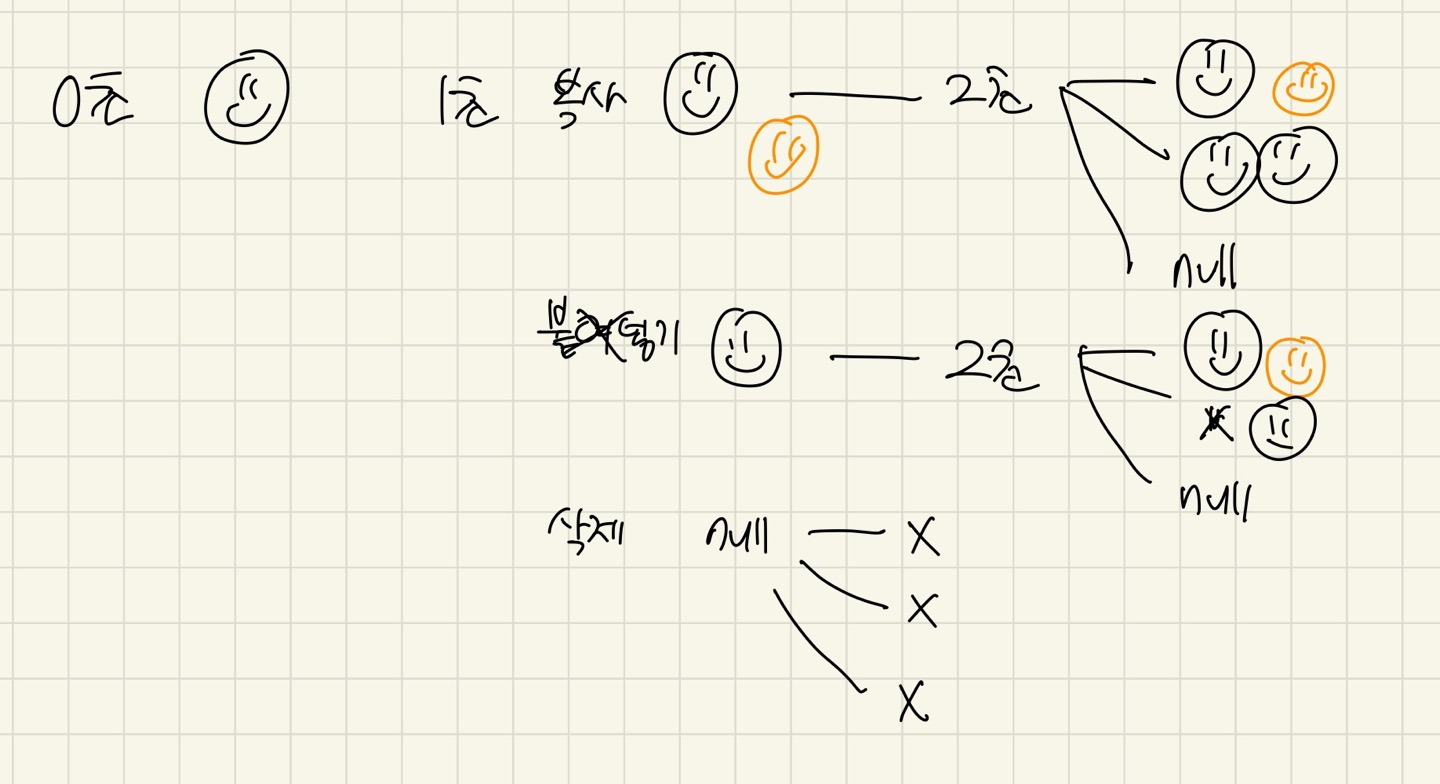
• 이런식으로 생각하다가
  
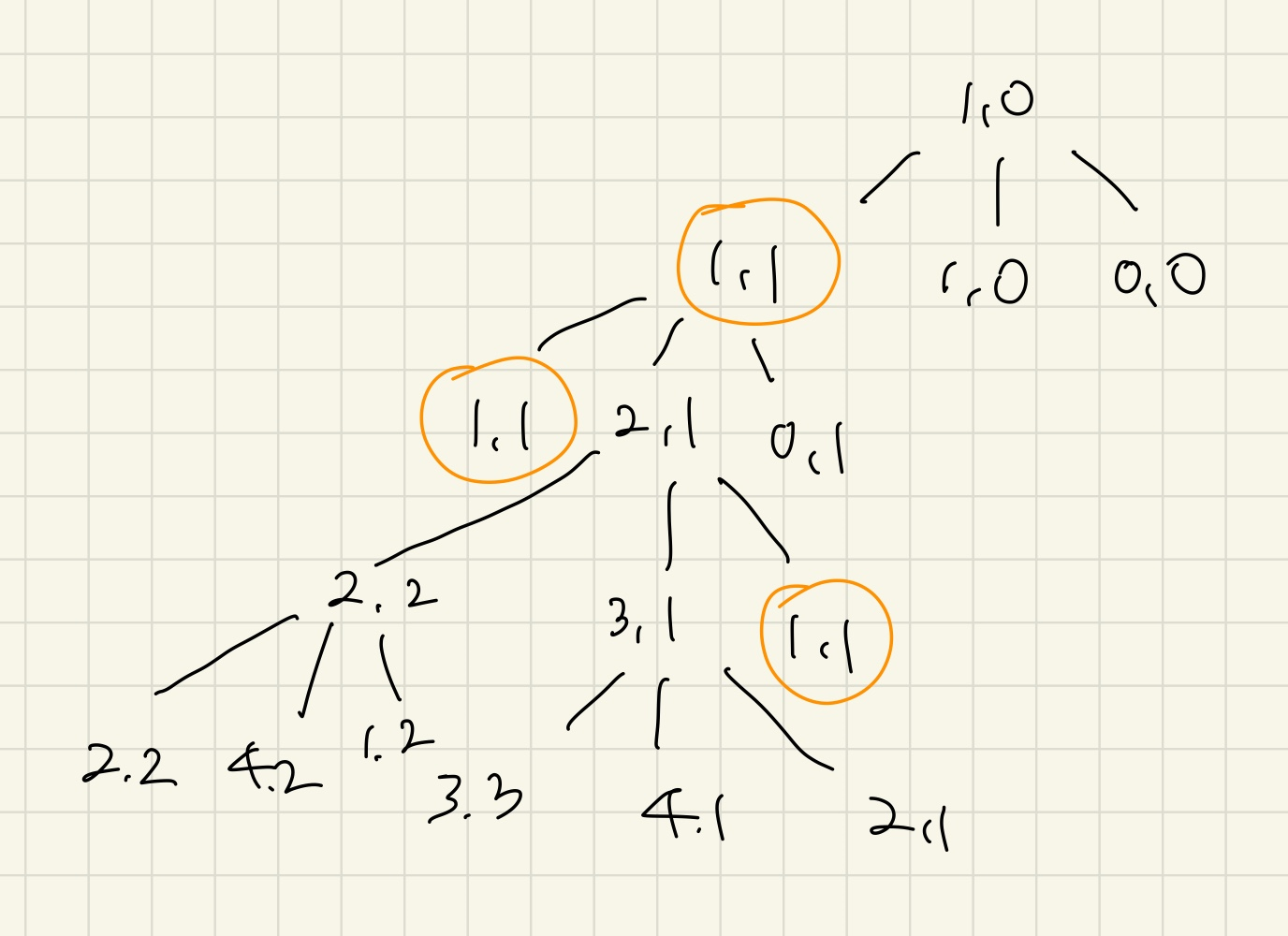
• 이렇게 까지 결국엔 (1,1) 을 보면 제일 위의 (1,1)이 최소값의 시간을 가지게 되니까 이중배열 boolean[스크린][클립보드]로 방문체크를 해주면 된다.
• 이런 문제를 보면 마음이 급해져서 심호흡을 하고 실수하지 않게 차근차근 작성하는게 ,, 중요하다 ! 괜히 오타나거나 변수 실수 있으면 보이지도 않음 (나 자신에게 주는 꿀팁)

Solution

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

// 이모티콘
class Emoticon {
	int screen; // 현재 화면의 이모티콘 개수
	int clipboard; // 복사한 클립보드의 이모티콘 개수
	int second; // 시간

	public Emoticon(int screen, int clipboard, int time) {
		this.screen = screen;
		this.clipboard = clipboard;
		this.second = time;
	}
}

public class Main {
	static int maxEmoCnt = 1001; // 화면이모티콘, 클리보드이모티콘
	static int S;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		S = sc.nextInt();

		bfs();
	}

	public static void bfs() {
		boolean[][] visited = new boolean[maxEmoCnt][maxEmoCnt];
		Queue<Emoticon> queue = new LinkedList<>();
		queue.add(new Emoticon(1, 0, 0));
		visited[1][0] = true; // 0초에 방문했으니 방문처리
		
		while (!queue.isEmpty()) {
			Emoticon emo = queue.poll();
			int screenN = emo.screen;
			int clipboardN = emo.clipboard;
			int time = emo.second;

			if (screenN == S) { // 화면에 S개가 만들어지면
				System.out.println(time);
				break;
			}

			// 복사
			if (screenN > 0 && !visited[screenN][screenN]) {
				visited[screenN][clipboardN] = true;
				queue.add(new Emoticon(screenN, screenN, time + 1)); // screen에 있는 이모티콘을 clipboard에 복사
			}
			// 붙여넣기
			if (clipboardN > 0 && (screenN + clipboardN) < maxEmoCnt && !visited[screenN + clipboardN][clipboardN]) {
				visited[screenN + clipboardN][clipboardN] = true;
				queue.add(new Emoticon(screenN + clipboardN, clipboardN, time + 1)); // clipboard에 있는 이모티콘을 screen에 더해줌
			}
			// 삭제
			if (screenN > 0 && !visited[screenN - 1][clipboardN]) {
				visited[screenN - 1][clipboardN] = true;
				queue.add(new Emoticon(screenN - 1, clipboardN, time + 1));
			}
		}

	}
}