
버블 정렬(bubble sort)
시간복잡도는 O(n^2)으로 느리지만, 코드가 단순하기 때문에 자주 사용된다. 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어진 이름이다. 양방향으로 번갈아 수행하면 칵테일 정렬이 된다.
위의 그림과 아래의 알고리즘는 버블 정렬을 오름차순으로 정렬한 것입니다.
- 마주한 두 배열의 요소를 비교하여 앞의 요솟값이 뒤의 요솟값보다 크면 교환(이러한 비교와 교환작업을 pass라고 한다.)
마주한 두개의 요소씩 비교함으로 첫번째는 pass 횟수가 n - 1회이며 배열에서 가장 큰 값이 9가 정렬되었습니다. 두번째는 n - 2회를 돌며 9 다음으로 큰 값인 8이 정렬됩니다. 이런식으로 pass 과정이 하나씩 줄어들어 총 pass 횟수는 (n - 1) + (n - 2) + ... + 1 = n(n - 1)/2회 입니다.
교환 횟수는 배열 요솟값에 영향을 받아 두 값을 비교할때 교환할 확률이 1/2이므로 평균 교환 횟수는 n(n - 1)/4회이며, 이동횟수는 swap()함수안에서 값의 이동이 한번 호출될때마다 3회씩 일어나므로 3n(n - 1)/4입니다.
#include <stdio.h>
#define swap(type, x, y) do { type t = x; x = y; y = t;} while(0)
void bubble(int a[], int n) {
for (int i = 0; i < n - 1; i++) { // 마주한 두개의 요소씩 비교함으로 i < n - 1
for (int j = 0; j < n - i - 1; j++) { // pass(비교, 교환)작업
// n - 1 : pass 수행할때 마다 정렬할 요소 하나씩 줄어듬
if (a[j] > a[j + 1]) { // 비교
swap(int, a[j + 1], a[j]); // 교환
}
}
}
}
버블 정렬 알고리즘 개선(1)
만약 아래 그림과 같이 4가 정렬된 이후 정렬을 마쳤다면 그 이후에 불필요한 pass과정(비교, 교환)을 돌게 됩니다. 따라서 교환횟수를 카운팅하는 변수를 활용하여 교환 횟수가 없을시에는 버블 정렬 반복문을 탈출시켜줍니다.
#define swap(type, x, y) do { type t = x; x = y; y = t;} while(0)
void bubble(int a[], int n) {
int exchg; // 교환 횟수
for (int i = 0; i < n - 1; i++) { // 마주한 두개의 요소씩 비교함으로 i < n - 1
exchg = 0; // pass 과정 끝날때 마다 교환 횟수 초기화
for (int j = 0; j < n - i - 1; j++) { // pass(비교, 교환)작업
// n - 1 : pass 수행할때 마다 정렬할 요소 하나씩 줄어듬
if (a[j] > a[j + 1]) { // 비교
swap(int, a[j + 1], a[j]); // 교환
exchg++; // 교환하면 교환횟수 카운팅
}
}
if (exchg == 0) // 교환 없을시
break;
}
}버블 정렬 알고리즘 개선(2)
아래 그림에서 교환없음 부분과 같이 이미 정렬되어있는 배열들을 비교하기 때문에 알고리즘에서 불필요한 비교가 반복됩니다. 따라서 마지막 교환한 요소의 인덱스를 저장하여 그 전까지만 비교할수 있도록 합니다.
#define swap(type, x, y) do { type t = x; x = y; y = t;} while(0)
void bubble(int a[], int n) {
int k = n - 1; // a[k] ~ a[n - 1]까지 정렬을 마친 상태
int last; // 마지막으로 교환한 인덱스
while (k > 0) {
last = 0; // 초기화 : 교환한 요소가 없을때 반복문 탈출
for (int j = 0; j < k; j++) { // 정렬 안된 요소까지 pass(비교, 교환)작업
if (a[j] > a[j + 1]) { // 비교
swap(int, a[j + 1], a[j]); // 교환
last = j; // 마지막으로 교환한 인덱스 저장
}
}
k = last; // 마지막으로 교환한 인덱스 대입
}
}변수 두개를 이용하여 pass작업을 거칠때마다 한 개의 변수(last) 교환한 요소의 마지막 인덱스를 저장하고 다른 한개의 변수(k)에 대입하여 마지막으로 교환한 요소 전까지만 pass작업을 할수있도록 합니다. 또한 last를 0으로 초기화 시켜서 모든 값들이 정렬된 직후에 k가 0이 되어서 반복문을 탈출되도록합니다.
양방향 버블 정렬(bidirection bubble sort)
다른 말로 칵테일 정렬(cocktail) 혹은 쉐이커 정렬(shaker sort)이라고 불린다.
정렬 아래와 같이 양방향으로 양쪽끝을 오가며 정렬이 안된 부분을 pass(비교, 교환)작업을 하며 진행됩니다.
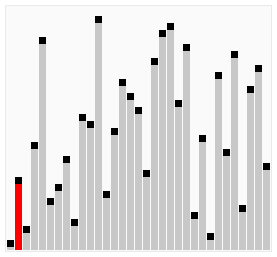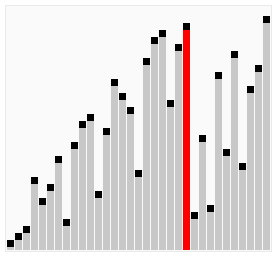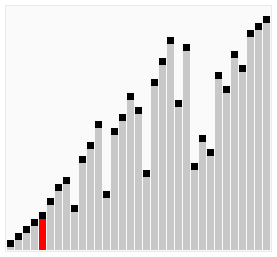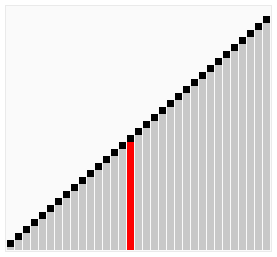
예를 들어 [2, 3, 4, 5, 6, 7, 1]과 같은 배열이 있을때, 위의 버블 정렬 알고리즘 개선(2)를 사용하여도 시간단축이 되지 않습니다. 그 이유는 한쪽 방향으로 pass(비교, 교환)작업을 거쳐 이동하기 때문입니다.
1이 맨 앞에 올때까지의 과정은 맨 처음 위치부터 1이 있는 위치까지 가서 1보다 큰 값과 교환하고 다시 처음으로 돌아가 반복하여 1이 맨 처음 위치에 올때까지 반복합니다. 아래 그림을 살펴보면 이해가 수월합니다.
버블정렬은 다시 맨처음으로 돌아가 pass(비교, 교환)하는 반면, 양방향 버블정렬은 맨 처음으로 돌아가지 않고 양쪽에 피봇해 놓은 마지막 교환 위치부터 pass(비교, 교환)합니다.
양방향 버블 정렬 코드입니다.
#define swap(type, x, y) do { type t = x; x = y; y = t;} while(0)
void shaker(int a[], int n)
{
int j;
int left = 0;
int right = n - 1;
int last = left;
// 양쪽 끝을 오가며 pass과정 거침
while (left < right) { // 왼쪽 피봇이 오른쪽 피봇보다 같거나 클때 종료
for (j = left; j < right; j++) { // 왼쪽 끝 부터
if (a[j] > a[j + 1]) { // 비교
swap(int, a[j], a[j + 1]); // 교환
last = j; // 오른쪽 마지막 교환값의 인덱스 저장
}
}
right = last; // 오른쪽의 마지막 교환값의 인덱스 피봇
for (j = right; j > left; j--) { // 왼쪽 끝 부터
if (a[j - 1] > a[j]) { // 비교
swap(int, a[j - 1], a[j]); // 교환
last = j; // 왼쪽의 마지막 교환값의 인덱스 저장
}
}
left = last; // 왼쪽의 마지막 교환값의 인덱스 피봇
}
}- 비교 작업 횟수
버블 정렬 : 21 = 6 + 5 + 4 + 3 + 2 + 1
양방향 버블 정렬 : 15 = 6 + 5 + 4
상대적으로 버블정렬보다 양방향 버블정렬이 빠른걸 볼수 있습니다.
- 양방향 버블 정렬 피봇과정
1) left = 0, right = n - 1
2) [왼쪽에서 오른쪽]비교회수 6회 : right = 5
3) [오른쪽에서 왼쪽]비교회수 5회 : left = 1
4) [왼쪽에서 오른쪽(이미 정렬 완료)]비교회수 4회 : right = 0
5) 종료 : left >= right
