병합 정렬(Merge Sort)

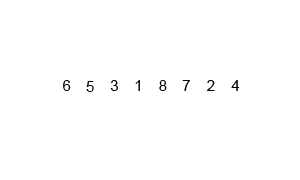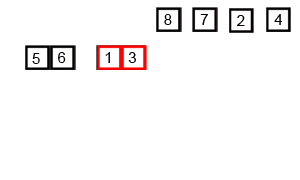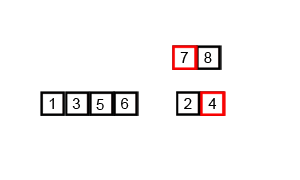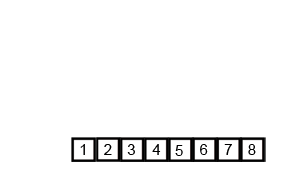
• 병합 정렬이란?
  하나의 큰 문제를 두개의 작은 문제로 분할한 뒤에 각자 계산하고 나중에 합치는 방법(일단 정확히 반으로 나누고 나중에 정렬)

• 병합 정렬 과정

1. 분할 : 배열을 같은 크기(n/2) 2개(왼쪽 부분, 오른쪽 부분)로 나눈다.
2. 정복 : 재귀함수 순환호출을 통한 분할&병합
3. 병합 : 왼쪽 부분, 오른쪽 부분 배열을 정렬하며 합침

분할하고 병합하는 것을 정복하는 병합정렬이며, 실행 순서는 (n)으로 표시되어 있다.

• 시간 복잡도 계산
  그림과 같이 각 k(병합 단계) 마다 분할된 배열의 개수 n이라 하면, 2^k(k = 1, 2, 3...)씩 늘어난다. 따라서 순환 호출의 깊이가 3임을 알 수 있다. 일반화하면 n=2^k의 경우, k=logn임을 알수 있다. 그리하여 순환 호출 횟수(병합 단계)는 logn번이고 요소의 개수가 n개 이므로 시간 복잡도는 O(nlogn)이다.

• 공간 복잡도 계산
  병합할 곳의 새로운 배열을 생성해줘야한다. 정렬할 배열과 같은 크기(n)의 새로운 배열이 필요하다. 따라서 공간복잡도는 O(2n)이다.

• 코드

/* 병합 정렬 프로그램 */
#pragma warning (disable:4996)
#include <stdio.h>
#include <stdlib.h>

static int *sorted;		/* 추가 배열(필요할때 마다 배열 생성시 비효율적임) */

/* 병합(combine) 정렬 */
void merge(int a[], int left, int mid, int right)
{
	int i = left; // 분할 된 왼쪽 그룹의 첫 인덱스
	int j = mid + 1; // 분할 된 오른쪽 그룹의 첫 인덱스(중앙요소 + 1)
	int k = left; // 병합할 위치(왼쪽 그룹의 첫 인덱스 위치와 같음)

	/* 작은 순서대로 배열에 삽입 */
	while (i <= mid && j <= right) { // 왼쪽 그룹은 중앙 요소까지, 오른쪽 그룹은 중앙요소 뒤부터 끝까지
		if (a[i] <= a[j]) // 왼쪽 그룹 요소가 오른쪽 그룹 요소 보다 클경우
			sorted[k++] = a[i++]; // 정렬한 배열에 저장
		else              // 오른쪽 그룹 요소가 왼쪽 그룹 요소 보다 클경우  
			sorted[k++] = a[j++]; // 정렬한 배열에 저장
	}

	/* 남은 데이터 삽입 */
	if (i > mid) { // 왼쪽 그룹 먼저 끝난 경우
		for (int t = j; t <= right; t++) // 오른쪽 그룹 삽입
			sorted[k++] = a[t];
	}
	else { // 오른쪽 그룹 먼저 끝난 경우
		for (int t = i; t <= mid; t++)
			sorted[k++] = a[t];
	}

	/* 정렬된 데이터를 삽입 */
	for (int t = left; t <= right; t++) 
		a[t] = sorted[t];
}

/*--- 병합 정렬(main 부분) ---*/
void mergesort(int a[], int left, int right)
{
	/* 정복(conquer) */
	if (left < right) { // 중단 조건(리스트 1개 까지만 분할)
		/* 분할(divide) */
		int mid = (left + right) / 2;

		mergesort(a, left, mid);		/* 왼쪽 부분에 대한 병합 정렬 */
		mergesort(a, mid + 1, right);		/* 오른쪽 부분에 대한 병합 정렬 */

		/* 병합(combine) */
		merge(a, left, mid, right); // 실제 정렬
	}
}

int main(void)
{
	int i, nx;
	int* x;				// 배열의 첫 번째 요소에 대한 포인터 

	scanf("%d", &nx);
	x = calloc(nx, sizeof(int)); // 배열 메모리 동적 할당 

	for (i = 0; i < nx; i++) 
		scanf("%d", &x[i]);
	
	if ((sorted = calloc(nx, sizeof(int))) == NULL)
		return -1;

	mergesort(x, 0, nx - 1);		/* 배열 전체를 병합 정렬 */

	free(sorted); /* 추가배열을 해제 */

	for (i = 0; i < nx; i++)
		printf("%d ", x[i]);

	free(x);		// 배열을 해제 

	return 0;
}

• 병합 정렬 장점

1. 시간 복잡도 O(nlogn)으로 굉장히 빠름
2. 서로 떨어져 있는 것을 교환 하는게 아니라서 안정적인 정렬

• 병합 정렬 단점

1. 임시의 배열 필요하므로, 추가 메모리 요구