알고리즘에 탐욕 기법을 활용할 수 있다.
문제를 볼 때 떠오르는 효율적인 선택이 탐욕 기법이다.
탐욕 기법을 사용할 때는 신중할 필요가 있다.
손님에게 거스름돈으로 주는 지폐와 동전의 개수를 최소화하는 아래 경우를 살펴보자.
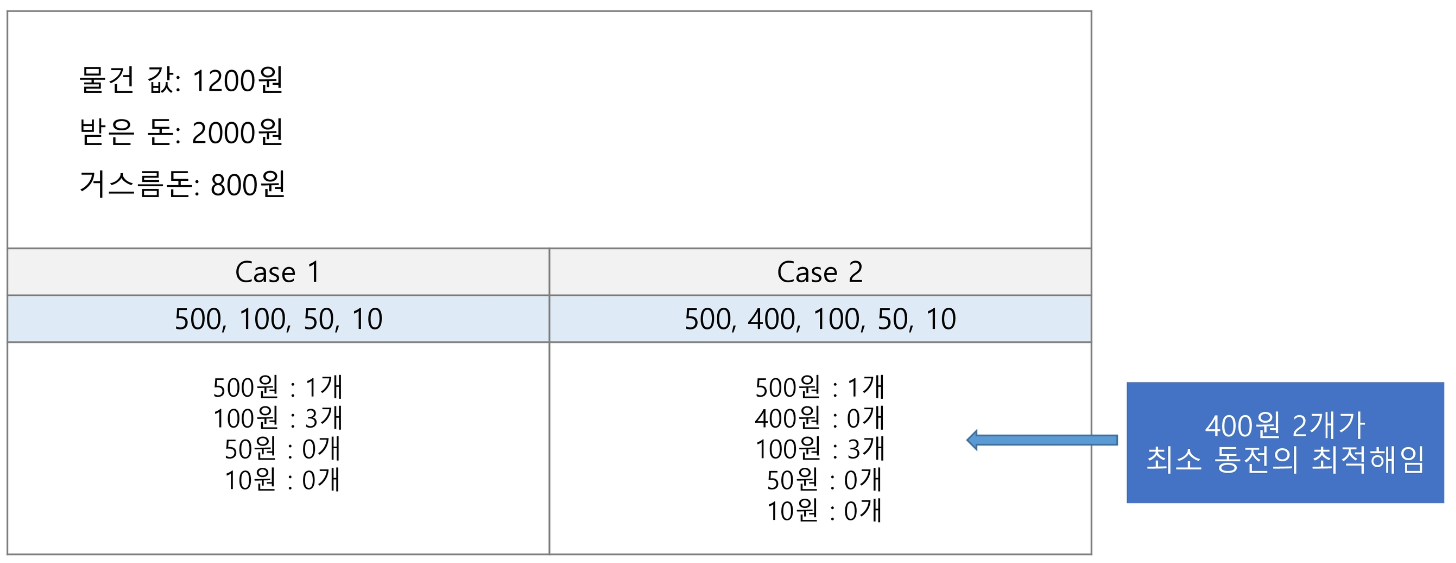
Case 1에는 가장 큰 단위의 화폐 먼저 거스름돈으로 주는 것으로 문제를 해결할 수 있다.
하지만 Case 2에는 그렇게 문제를 해결할 수 없다. 따라서 증명된 경우에만 탐욕 기법을 사용해야 한다.
0-1 배낭 문제는 탐욕 기법으로 풀 수 없다.
0-1 배낭 문제의 정의는 아래와 같다.
무게와 가치가 다양한 물건들이 있다.
이 때, 배낭에 담을 수 있는 무게가 정해진 상황에서 최대의 가치를 얻는 방법은 무엇인가?
(물건을 쪼개서 담을 순 없다.)
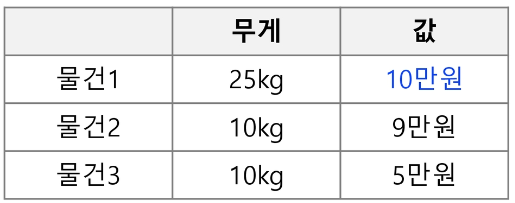
이 문제를 풀 때 생각할 수 있는 탐욕 기법은 아래와 같다. W = 30kg이다.
- 값이 비싼 물건부터 채운다.
탐욕 기법 결과 : (물건 1) -> 10만원
최적해 : (물건 2, 물건 3) -> 14만원
따라서 탐욕 기법으로 최적해를 찾을 수 없다.
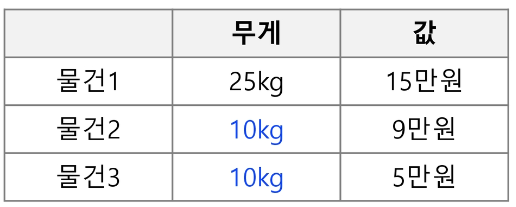
- 무게가 가벼운 물건부터 채운다.
탐욕 기법 결과 : (물건 2, 물건 3) -> 14만원
최적해 : (물건 1) -> 15만원
따라서 탐욕 기법으로 최적해를 찾을 수 없다.
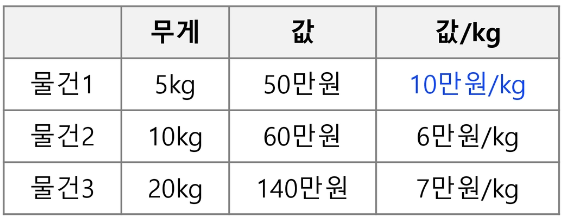
- 무게 당 값이 높은 물건부터 채운다.
탐욕 기법 결과 : (물건 1, 물건 3) -> 190만원
최적해 : (물건 2, 물건 3) -> 200만원
따라서 탐욕 기법으로 최적해를 찾을 수 없다.
즉, 탐욕 기법으로 문제를 풀 수 없다.
회의실 배정 문제는 탐욕 기법으로 풀 수 있다.
회의실 배정 문제의 정의는 아래와 같다.
시작 시간과 종료 시간이 다양한 회의들이 있다.
이 때, 회의 시간이 겹치면 안 되는 경우 최대로 열 수 있는 회의는 얼마인가?
이 문제에 적용할 수 있는 탐욕 기법은 아래와 같다.
- 종료 시간 순으로 회의들을 정렬한다.
- 첫번째 회의를 선택한다.
- 선택한 회의보다 시작 시간이 빠른 회의들은 무시하고, 선택한 회의가 끝난 뒤 시작이 가장 빠른 회의를 선택한다.
- 3번을 정해진 시간 안에 반복한다.
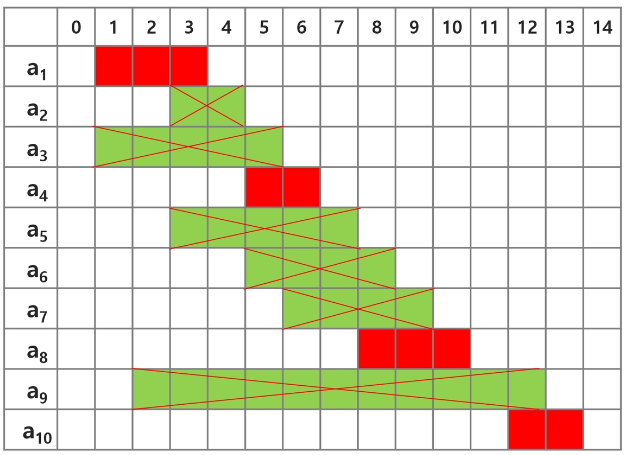
이를 적용해서 문제를 해결하면 아래와 같다.
a1, a4, a8, a10이 선택됐으므로 최대 4개의 회의를 열 수 있다.
0-1 배낭 문제에서 탐욕 기법을 쓸 수 없지만,
회의실 배정 문제에서 탐욕 기법을 쓸 수 있던 이유는 아래와 같다.
0-1 배낭 문제에서 물건1을 선택한 후, 물건3을 선택하면 최적해를 찾을 수 없다.
하지만 회의실 배정 문제에서 a1을 선택한 후, a4를 선택해도 최적해를 찾을 수 있다.
이를 일반화한 탐욕 기법의 조건은 아래와 같다.
탐욕적 선택을 한 후 남은 문제의 최적해가 원 문제의 최적해랑 같아야 한다.
알고리즘에서 대우를 활용할 수 있다.
아래 문제는 동전 자판기라는 문제다. 문제를 살펴보자.
나동전씨는 500원, 100원, 50원, 10원, 5원, 1원 동전을 가지고 다닌다.
이 때 동전을 최대한 많이 써서 정확한 액수를 지불해 음료수를 구매하고자 한다.
위의 경우일 때 사용하는 동전 수와 동전 종류를 출력해라.
이 문제에 생각할 수 있는 탐욕 기법은 아래와 같다.
단위가 가장 작은 코인부터 순차적으로 모두 사용한다.
이 방법은 단위가 가장 작은 코인을 순차적으로 사용하면 정확한 액수를 맞추지 못한다는 문제가 있다.
따라서 동전을 최대한 많이 써서 정확한 액수를 지불한다는 것이 아닌,
해당 동전들로 가능한 가장 큰 액수에서 동전을 최대한 적게 써서
정확한 액수를 지불할 동전들의 갯수를 구한다 라고 풀 수 있다.
이를 구현하면 아래와 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int W = Integer.parseInt(br.readLine());
int[] arr = new int[6];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < 6; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int max = 0;
int[] valueArr = {500, 100, 50, 10, 5, 1}; // 동전 종류
for (int i = 0; i < 6; i++) {
max += arr[i] * valueArr[i]; // 최대 값
}
int outside = max - W; // 동전을 최대한 작게 써서 맞춰야하는 값
while (arr[0] > 0 && outside >= 500) {
outside = outside - 500;
arr[0]--;
}
while (arr[1] > 0 && outside >= 100) {
outside = outside - 100;
arr[1]--;
}
while (arr[2] > 0 && outside >= 50) {
outside = outside - 50;
arr[2]--;
}
while (arr[3] > 0 && outside >= 10) {
outside = outside - 10;
arr[3]--;
}
while (arr[4] > 0 && outside >= 5) {
outside = outside - 5;
arr[4]--;
}
while (arr[5] > 0 && outside >= 1) {
outside = outside - 1;
arr[5]--;
}
int sum = 0;
for (int i = 0; i < 6; i++) {
sum += arr[i];
}
System.out.println(sum);
for (int i = 0; i < 6; i++) {
System.out.print(arr[i] + " ");
}
}
}이런 식으로 알고리즘에 명제의 대우를 활용할 수 있다.