Algorithm 11일차

알고리즘에 분할 정복 기법을 적용할 수 있다.

분할 정복 기법이란 분할, 정복, 통합을 거치는 문제 해결 기법이다.
정확한 정의는 아래와 같다.

1. 분할 : 해결할 문제를 여러 개의 작은 부분으로 나눈다.
2. 정복 : 나눈 작은 문제를 각각 해결한다.
3. 통합 : (필요하다면) 해결된 해답을 모은다.

거듭 제곱 문제에 분할 정복 기법을 적용할 수 있다.
거듭 제곱 문제를 두 가지 방식으로 풀어보자.

1. 반복문 또는 재귀

// 재귀 함수
public static long exp(long x, long n) {
	if (n == 1) {
		return x;
	}
	return x * exp(x, n - 1);
}

// main 함수
public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int x = sc.nextInt();
	int n = sc.nextInt(); 
	System.out.println(exp(x, n));
	sc.close();
}

시간 복잡도는 O(n)이다.

2. 분할 정복 기법

// 분할 정복 함수
public static long exp(long x, long n) {
	if (n == 1) return x;	
	long y = exp(x, n/2);
	if (n % 2 == 0) {
		return y * y;
	} else {
		return y * y * x;
	}
}

// main 함수
public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int x = sc.nextInt();
	int n = sc.nextInt(); 
	System.out.println(exp(x, n));
	sc.close();
}

시간 복잡도는 O(log(N))이다.

같은 색 공간 만들기 문제에 분할 정복 기법을 적용할 수 있다.
같은 색 공간 만들기의 문제 정의는 아래와 같다.

1. 전체 공간의 크기는 N*N (N = 2, 4, 8, 16 ...) 이다.
2. 전체 공간이 같은 색으로 이뤄져있으면 자르지 않고,
   같은 색으로 이뤄져 있지 않다면 N/2로 나눈다.
3. 2번 과정을 공간이 같은 색으로만 이뤄져 있을 때까지 반복한다.
4. 하얀색으로 이뤄진 공간 수, 초록색으로 이뤄진 공간 수를 각각 출력한다.

아래는 위 규칙처럼 공간을 나눈 예시이다.

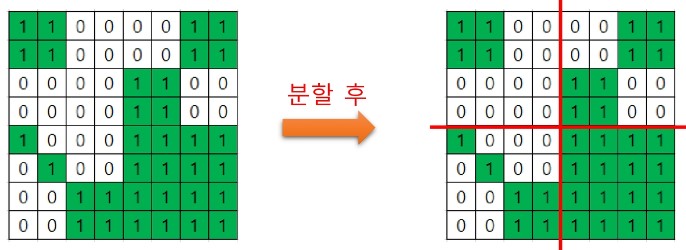
오른쪽 아래 공간처럼 공간이 같은 색으로만 남을 때까지 분할을 반복한다.

해당 문제의 풀이 코드는 아래와 같다.

import java.util.Scanner;

public class MakeSpace {
	static int white = 0;
	static int green = 0;
	static int[][] spaces;
	
	static void cut(int r, int c, int size) {
		int sum = 0;
		
		for (int i = r, rEnd = r + size; i < rEnd; i++) {
			for (int j = c, cEnd = c + size; j < cEnd; j++) {
				sum += spaces[i][j];
			}
		}
		
		if (sum == size * size) {
			green++;
		} else if (sum == 0) {
			white++;
		} else {
			int half = size / 2;
			
			cut(r, c, half);
			cut(r, c + half, half);
			cut(r + half, c, half);
			cut(r + half, c + half, half);
		}
	}

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		spaces = new int[n][n];
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				spaces[i][j] = sc.nextInt();
			}
		}
		
		cut(0, 0, n);
		
		System.out.println(white);
		System.out.println(green);
		sc.close();
	}
}

출력 결과는 아래와 같다.

9
7

알고리즘에서 이진 검색을 활용할 수 있다.

이진 검색의 정의는 아래와 같다.

찾고자 하는 값을 배열의 중앙값과 비교하여 검색 범위를 반으로 줄여 검색을 일반 검색보다 빨리 수행하는 방법이다.

이진 검색의 특징은 아래와 같다.

이진 검색은 정렬이 되어 있을 때 시간 복잡도가 O(log(N))이며,
정렬이 안 되어있다면 O(Nlog(N)) 시간 복잡도의 정렬을 수행해야 하므로
일반 검색인 O(N)보다 손해이다.

이진 검색은 반복문, 재귀 두 가지 모두 구할 수 있다.
이진 검색을 구현한 코드는 아래와 같다.

public class BinarySearch {
	private static int[] values = {3, 11, 15, 20, 21, 29, 45, 59, 65, 72, 78, 86, 92, 95};
	
	static int bs1(int key) { // 반복문
		int mid, start, end;
		start = 0;
		end = values.length - 1;
		
		while (start <= end) {
			mid = (start + end) / 2;
			if (values[mid] == key) {
				return mid;
			} else if (values[mid] < key) {
				start = mid + 1;
			} else {
				end = mid - 1;
			}
		}
		
		return -1;
	}
	
	static int bs2(int start, int end, int key) { // 재귀
		if (start > end) {
			return -1;
		}
		
		int mid = (start + end) / 2;
		
		if (values[mid] == key) {
			return mid;
		}
		
		if (key > values[mid]) {
			return bs2(mid + 1, end, key);
		} else {
			return bs2(start, mid - 1, key);
		}
	}
	
	public static void main(String[] args) {
		int idx1 = bs1(45);
		System.out.println(idx1);
		int idx2 = bs2(0, 13, 45);
		System.out.println(idx2);
	}
}	

출력 결과는 아래와 같다.

6
6