Algorithm 15일차

알고리즘에서 그래프를 dfs로 완전 탐색할 수 있다.

그래프에서 dfs는 아래와 같이 진행된다.

1. 시작 정점을 잡고, 해당 정점을 방문한다.
2. 해당 정점을 방문했음을 표시한다.
3. 방문한 정점의 모든 정점을 살펴본다.
4. 살펴보다가 방문하지 않은 정점을 방문할 시 그 정점을 기준으로 1, 2, 3 과정을 반복한다.

알고리즘에서 인접 행렬를 dfs로 완전 탐색할 수 있다.

아래와 같은 그래프가 있다.

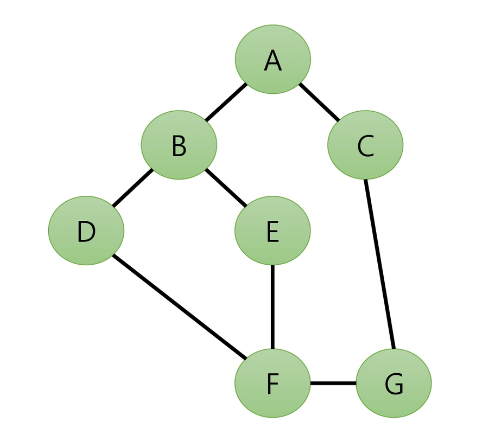
위 그래프가 인접 행렬로 표현되어 있을 때, dfs로 완전 탐색하는 코드는 아래와 같다.

import java.util.Scanner;

public class MatrixDFS {
	static int[][] adjMatrix;
	static int V;
	
	static void dfs(int current, boolean[] visited) {
		visited[current] = true;
		System.out.print((char)(current + 65) + " ");
		
		for (int i = 0; i < V; i++) {
			if (adjMatrix[current][i] != 0 && !visited[i]) {
				dfs(i, visited);
			}
		}
	}
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		V = sc.nextInt();
		int E = sc.nextInt();
		
		adjMatrix = new int[V][V];
		
		int from, to;
		
		for (int i = 0; i < E; i++) {
			from = sc.nextInt();
			to = sc.nextInt();
			
			adjMatrix[from][to] = adjMatrix[to][from] = 1;
		}
		
		dfs(0, new boolean[V]);
		
		sc.close();
	}
}	

입력값과 출력 결과는 아래와 같다.

1. 입력값
   7
   8
   0 1
   0 2
   1 3
   1 4
   3 5
   4 5
   5 6
   2 6

2. 출력 결과
   A B D F E G C

알고리즘에서 인접 리스트를 dfs로 완전 탐색할 수 있다.

위 그래프가 Node 클래스를 직접 구현한 인접 리스트로 표현되어 있을 때,
dfs로 완전 탐색하는 코드는 아래와 같다.

import java.util.Scanner;

public class ListBFS {
	static Node[] adjList;
	static int V;
	
	static class Node {
		int V;
		Node node;
		
		public Node(int v, Node node) {
			super();
			V = v;
			this.node = node;
		}
		
		@Override
		public String toString() {
			return "Node [V=" + V + ", node=" + node + "]";
		}
	}
	
	static void dfs(int current, boolean[] visited) {
		visited[current] = true;
		System.out.print((char)(current + 65) + " ");
		
		for (Node node = adjList[current]; node != null; node = node.node) {
			if (visited[node.V] != true) {
				dfs(node.V, visited);
			}
		}
	}
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		V = sc.nextInt();
		int E = sc.nextInt();
		
		adjList = new Node[V];
		
		int from, to;
		
		for (int i = 0; i < E; i++) {
			from = sc.nextInt();
			to = sc.nextInt();
			
			adjList[from] = new Node(to, adjList[from]);
			adjList[to] = new Node(from, adjList[to]);
		}
		
		dfs(0, new boolean[V]);
		
		sc.close();
	}
}

입력값과 출력 결과는 아래와 같다.

1. 입력값
   7
   8
   0 1
   0 2
   1 3
   1 4
   3 5
   4 5
   5 6
   2 6

2. 출력 결과
   A C G F E B D

위 그래프가 List를 이용한 인접 리스트로 표현되어 있을 때,
dfs로 완전 탐색하는 코드는 아래와 같다.

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class ListDFS2 {
	static List<Integer>[] adjList;
	static int V;
	
	static void dfs(int current, boolean[] visited) {
		visited[current] = true;
		System.out.print((char)(current + 65) + " ");
		
		for (int value : adjList[current]) {
			if (visited[value] != true) {
				dfs(value, visited);
			}
		}
	} 
	
	public static void main(String[] args) {	
		Scanner sc = new Scanner(System.in);
		
		V = sc.nextInt();
		int E = sc.nextInt();
		
		adjList = new ArrayList[V];
		
		for (int i = 0; i < V; i++) {
			adjList[i] = new ArrayList<Integer>();
		}
		
		int from, to;
		
		for (int i = 0; i < E; i++) {
			from = sc.nextInt();
			to = sc.nextInt();
			
			adjList[from].add(to);
			adjList[to].add(from);
		}
		
		dfs(0, new boolean[V]);
		
		sc.close();
	}
}

입력값과 출력 결과는 아래와 같다.

1. 입력값
   7
   8
   0 1
   0 2
   1 3
   1 4
   3 5
   4 5
   5 6
   2 6

2. 출력 결과
   A B D F E G C