Algorithm 17일차

알고리즘에서 최소 신장 트리를 활용할 수 있다.

신장 트리란 n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이뤄진 트리이다.

최소 신장 트리란 무향 가중치 그래프에서 간선들의 가중치 합이 최소인 신장 트리이다.
최소 신장 트리의 예시는 아래와 같다.

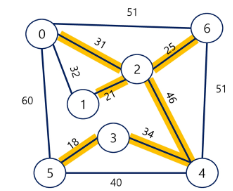
최소 신장 트리가 이뤄질 모든 경우를 찾게되면 그 경우의 수는 eCv-1이다.
즉, 간선이 30개이고 정점이 16개면 30C15로 시간 복잡도가 터지게 된다.
그래서 KRUSKAL 알고리즘과 PRIM 알고리즘을 활용한다.

최소 신장 트리를 구하는 데 KRUSKAL 알고리즘을 활용할 수 있다.

KRUSKAL 알고리즘은 아래와 같다.

1. 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
2. 가중치가 가장 낮은 간선부터 선택하며 트리를 증가시킨다.
   (이 때, 사이클이 존재하면 그 다음 간선으로 넘어간다.)
3. n-1개의 정점이 선택될 때까지 2를 반복한다.

정점의 서로소 집합이 합쳐지지 않으면 사이클이라고 생각하여 사이클을 검사한다.
이를 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Kruskal {
	static int[] set;
	static int n;
	
	static class Edge implements Comparable<Edge> {
		int from;
		int to;
		int weight;
		
		public Edge(int from, int to, int weight) {
			super();
			this.from = from;
			this.to = to;
			this.weight = weight;
		}

		@Override
		public int compareTo(Edge e) {
			return this.weight - e.weight;
		}
	}
	
	static void makeSet() {
		for (int i = 0; i < n; i++) {
			set[i] = i;
		}
	}
	
	static boolean unionSet(int first, int second) {
		int one = findSet(first);
		int two = findSet(second);
		
		if (one == two) {
			return false;
		} 
		
		set[two] = one;
		return true;
	}
	
	static int findSet(int find) {
		if (set[find] == find) {
			return find;
		}
		
		return set[find] = findSet(set[find]);
	}
	
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		n = Integer.parseInt(st.nextToken());
		int order = Integer.parseInt(st.nextToken());
		
		Edge[] edgeList = new Edge[order];
		
		for (int i = 0; i < order; i++) {
			st = new StringTokenizer(br.readLine());
			
			int first = Integer.parseInt(st.nextToken());
			int second = Integer.parseInt(st.nextToken());
			int third = Integer.parseInt(st.nextToken());
			
			edgeList[i] = new Edge(first, second, third);
		}
		
		Arrays.sort(edgeList);
		
		set = new int[n];
		
		makeSet();
		
		int result = 0;
		int check = 0;
		
		for (Edge edge : edgeList) {
			if (unionSet(edge.from, edge.to)) {
				result += edge.weight;
				check++;
				
				if (check == n - 1) {
					break;
				}
			}
		}
		
		System.out.println(result);
	}
}

입력값과 출력 결과는 아래와 같다.

1. 입력값
   7 11
   0 1 32
   0 2 31
   0 5 60
   0 6 51
   1 2 21
   2 4 46
   2 6 25
   3 4 34
   3 5 18
   4 5 40
   4 6 51

2. 출력 결과
   175

이 때, 여러 연산 중 정렬이 Elog(E)로 시간 복잡도가 가장 크다.
따라서 KRUSKAL 알고리즘은 간선 수가 많으면 효율적이지 않다.

최소 신장 트리를 구하는 데 Prim 알고리즘을 활용할 수 있다.

Prim 알고리즘은 아래와 같다.

1. 초기에는 모든 정점 간 관계가 무한대이다.
2. 임의의 정점을 하나 선택한다.
3. 선택한 정점(들)과 인접하는 정점(들)의 최소 비용을 갱신한다.
4. 선택한 정점(들)과 인접한 정점(들) 중 최소 비용으로 연결되는 정점 하나를 선택한다.
5. 모든 정점이 연결될 때까지 3, 4를 반복한다.

이를 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Prim {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		
		int[][] arr = new int[n][n];
		
		for (int i = 0; i < n; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			
			for (int j = 0; j < n; j++) {
				arr[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		
		boolean[] V = new boolean[n];
		
		int[] D = new int[n];
		for (int i = 0; i < n; i++) {
			D[i] = Integer.MAX_VALUE;
		}
		
		D[0] = 0;
		int result = 0;
		
		for (int i = 0; i < n; i++) {
			int minValue = Integer.MAX_VALUE;
			int minIndex = -1;
			
			for (int j = 0; j < n; j++) {
				if (V[j] == false && D[j] < minValue) {
					minValue = D[j];
					minIndex = j;
				}
			}
			
			V[minIndex] = true;
			result += minValue;
			
			for (int j = 0; j < n; j++) {
				if (V[j] == true || arr[minIndex][j] == 0) {
					continue;
				}
				
				if (D[j] > arr[minIndex][j]) {
					D[j] = arr[minIndex][j];
				}
			}
		}
		
		System.out.println(result);
	}
}

입력값과 출력 결과는 아래와 같다.

1. 입력값
   7
   0 32 31 0 0 60 51
   32 0 21 0 0 0 0
   31 21 0 0 46 0 25
   0 0 0 0 34 18 0
   0 0 46 34 0 40 51
   60 0 0 18 40 0 0
   51 0 25 0 51 0 0

2. 출력 결과
   175

이 때의 시간 복잡도는 O(V^2)이다.
따라서 간선 수가 많으면 비효율적인 KRUSKAL 알고리즘의 단점을 극복했다.

PRIM 알고리즘을 우선순위 큐로 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class PrimPriority {
	
	static class Data implements Comparable<Data> {
		int idx;
		int weight;
		
		public Data(int idx, int weight) {
			super();
			this.idx = idx;
			this.weight = weight;
		}

		@Override
		public int compareTo(Data d) {
			return this.weight - d.weight;
		}
	}
	
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		
		int[][] arr = new int[n][n];
		for (int i = 0; i < n; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			
			for (int j = 0; j < n; j++) {
				arr[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		
		boolean[] v = new boolean[n];
		
		int[] d = new int[n];
		for (int i = 0; i < n; i++) {
			d[i] = Integer.MAX_VALUE;
		}
		
		int start = 3;
		d[start] = 0;
		PriorityQueue<Data> pq = new PriorityQueue<>();
		pq.offer(new Data(start, 0));
		
		int result = 0;
		int res = 0;
		
		while(!pq.isEmpty()) {
			Data data = pq.poll();
			
			if (v[data.idx] == true) { 
				continue;
			}
			
			v[data.idx] = true;
			result += data.weight;
			res++;
			if (res == n) {
				break;
			}
			
			for (int i = 0; i < n; i++) {
				if (v[i] == false && arr[data.idx][i] != 0 && arr[data.idx][i] < d[i]) {
					d[i] = arr[data.idx][i];
					pq.offer(new Data(i, d[i]));
				}
			}
		}
		System.out.println(result);
	}
}

입력값과 출력 결과는 아래와 같다.

1. 입력값
   7
   0 32 31 0 0 60 51
   32 0 21 0 0 0 0
   31 21 0 0 46 0 25
   0 0 0 0 34 18 0
   0 0 46 34 0 40 51
   60 0 0 18 40 0 0
   51 0 25 0 51 0 0

2. 출력 결과
   175