Algorithm 18일차

알고리즘에서 다익스트라 알고리즘을 활용할 수 있다.

알고리즘에서 시작 정점에서 다른 모든 정점으로의 최단 경로 비용을 구해야 할 때가 있다.
아래는 이 같은 상황을 보여준다.

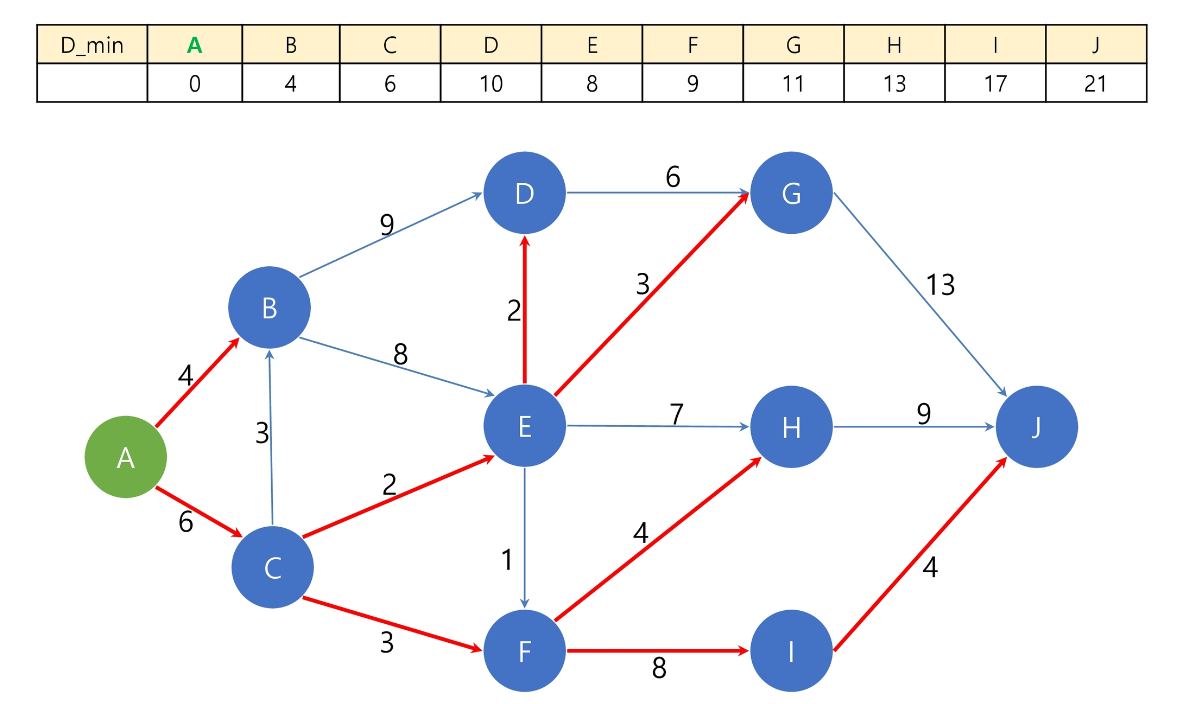
이 때 다익스트라 알고리즘을 활용할 수 있다.

다익스트라 알고리즘을 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Dijkstra {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int V = Integer.parseInt(br.readLine());
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		int start = Integer.parseInt(st.nextToken());
		int end = Integer.parseInt(st.nextToken());
		
		int[][] adjMatrix = new int[V][V];
		for (int i = 0; i < V; i++) {
			st = new StringTokenizer(br.readLine());
			
			for (int j = 0; j < V; j++) {
				adjMatrix[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		
		final int INF = Integer.MAX_VALUE;
		int[] distance = new int[V];
		boolean[] visited = new boolean[V];
		
		Arrays.fill(distance, INF);
		distance[start] = 0;
		
		int min, current;
		
		for (int c = 0; c < V; c++) {
			current = -1;
			min = INF;
			
			for (int i = 0; i < V; i++) {
				if (!visited[i] && min > distance[i]) {
					min = distance[i];
					current = i;
				}
			}
			
			if (current == -1 || current == end) {
				break;
			}
			visited[current] = true;
			
			for (int j = 0; j < V; j++) {
				if (!visited[j] && adjMatrix[current][j] != 0 && distance[j] > distance[current] + adjMatrix[current][j]) {
					distance[j] = distance[current] + adjMatrix[current][j];
				}
			}
		}
		
		if (distance[end] != INF) {
			System.out.println(distance[end]);
		} else {
			System.out.println("-1");
		}
	}
}

입력값과 출력 결과는 아래와 같다.

입력값
5
0 4
0 2 2 5 9
2 0 3 4 8
2 3 0 7 6
5 4 7 0 5
9 8 6 5 0

출력 결과
8

다익스트라 알고리즘을 우선순위 큐로 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class DijkstraPQ {
	static class Data implements Comparable<Data> {
		int idx;
		int weight;
		
		public Data(int idx, int weight) {
			super();
			this.idx = idx;
			this.weight = weight;
		}

		@Override
		public String toString() {
			return "Data [idx=" + idx + ", weight=" + weight + "]";
		}

		@Override
		public int compareTo(Data d) {
			return this.weight - d.weight;
		}
	}
	
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int V = Integer.parseInt(br.readLine());
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		int start = Integer.parseInt(st.nextToken());
		int end = Integer.parseInt(st.nextToken());
		
		int[][] adjMatrix = new int[V][V];
		for (int i = 0; i < V; i++) {
			st = new StringTokenizer(br.readLine());
			
			for (int j = 0; j < V; j++) {
				adjMatrix[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		
		final int INF = Integer.MAX_VALUE;
		int[] distance = new int[V];
		boolean[] visited = new boolean[V];
		
		Arrays.fill(distance, INF);
		distance[start] = 0;
		
		PriorityQueue<Data> pq = new PriorityQueue<>();
		pq.offer(new Data(start, 0));
		
		while (!pq.isEmpty()) {
			Data cur = pq.poll();
			
			if (visited[cur.idx] == true) {
				continue;
			}
			
			if (cur.idx == end) {
				break;
			}
			visited[cur.idx] = true;
			
			for (int j = 0; j < V; j++) {
				if (!visited[j] && adjMatrix[cur.idx][j] != 0 && distance[j] > cur.weight + adjMatrix[cur.idx][j]) {
					distance[j] = cur.weight + adjMatrix[cur.idx][j];
					pq.offer(new Data(j, distance[j]));
				}
			}
		}
		
		if (distance[end] != INF) {
			System.out.println(distance[end]);
		} else {
			System.out.println("-1");
		}
	}
}

입력값과 출력 결과는 아래와 같다.

입력값
5
0 4
0 2 2 5 9
2 0 3 4 8
2 3 0 7 6
5 4 7 0 5
9 8 6 5 0

출력 결과
8

※ 다익스트라 알고리즘은 음의 가중치는 허용하지 않는다. 아래와 같은 상황 때문이다.

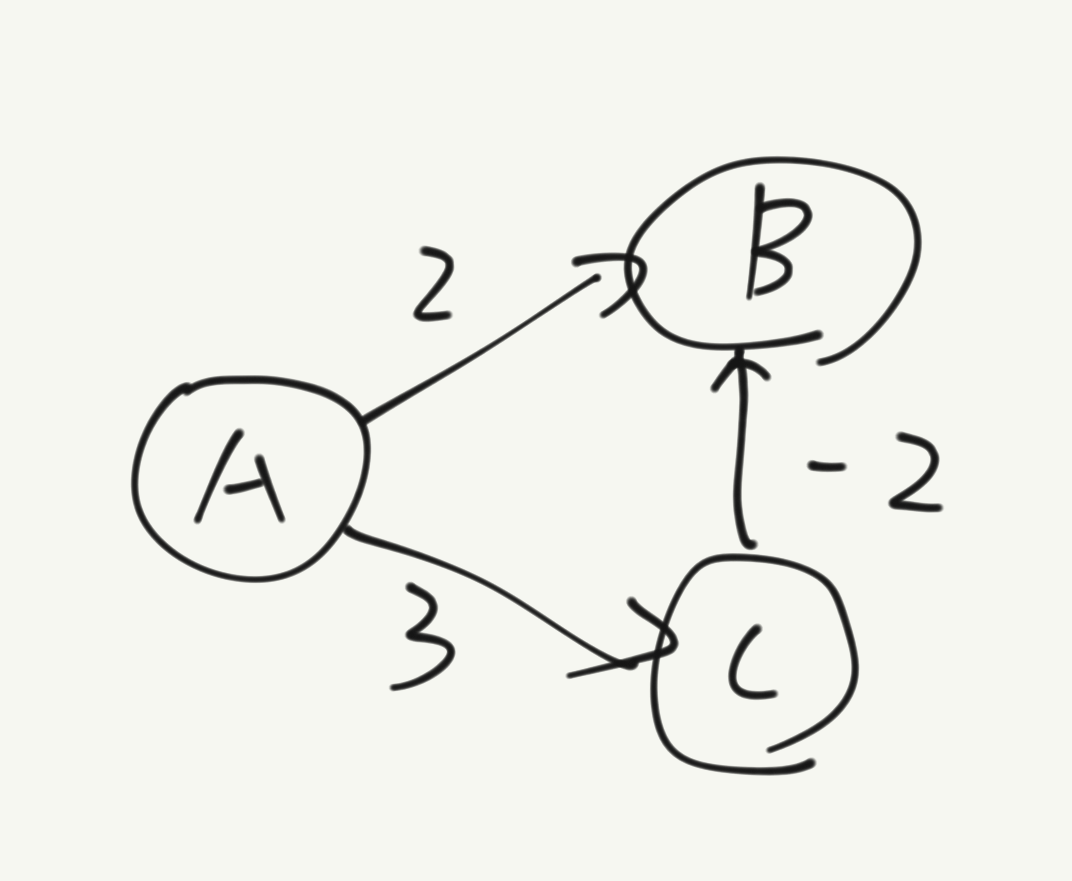
위 상황에서 다익스트라 알고리즘을 사용해서 A에서 B까지의 최단 경로 비용을 구해보자.
아마 A에서 출발하여 가중치 2로 B에 도달할 수 있다고 확정할 것이다.
그러나 실제로는 A -> C -> B를 거쳐 가중치 1로 B에 도달할 수 있다.
이런 예외사항 때문에 다익스트라 알고리즘은 음의 가중치를 허용하지 않는다.