알고리즘에서 0-1 배낭 문제를 1차원 DP로 해결할 수 있다.
0-1 배낭 문제를 2차원 DP로 풀면 아래와 같다.
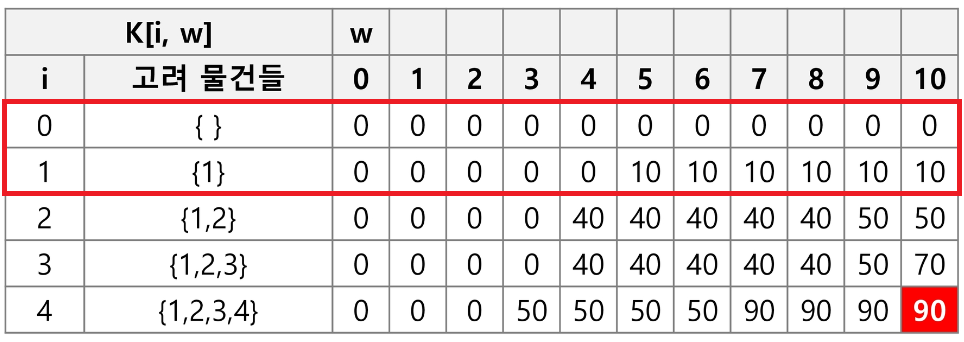
그 중 빨간 네모박스에 집중해보자. 아래와 같이 생각할 수 있다.
- i=0에 저장된 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 을 그대로 i=1에 사용한다.
- w=10부터 w=i's weight까지 max(K[i, w - i's weight] + i's price, K[i, w])
위 과정을 물건의 개수만큼 수행하면 arr[10]은 최적해가 된다.
따라서 0-1 배낭 문제를 1차원 배열로도 추적할 수 있다.
알고리즘에서 최장 증가 수열의 길이를 DP로 해결할 수 있다.
최장 증가 수열의 길이 문제의 정의는 아래와 같다.
3, 2, 6, 4, 5, 1 같은 배열이 있다.
이 때, 이 배열 순서는 유지하면서 크기가 점진적으로 커지는 가장 긴 부분수열의 길이는 얼마인가?
첫번째 방법은 부분 집합이다.
모든 부분 집합을 구하고 크기가 점진적으로 증가하는지 확인한다.

시간 복잡도는 O(2^n) 이다.
두번째 방법은 DP이다. 아래와 같이 풀 수 있다.
- 0 <= i < n 까지 LIS(i) = 1 + max(LIS(j)) (j < i and aj < ai)로 모든 경우의 LIS를 구한다.
- 가장 긴 LIS를 반환한다.
그럼 아래와 같이 생각할 수 있다.
- LIS(i)가 ai를 부분 수열의 마지막으로 포함하지 않는 경우
- LIS(i)가 ai를 부분 수열의 마지막으로 포함된 경우
1번 경우를 생각해보자. 그러면 LIS(i-1) = LIS(i)라고 생각할 수 있다.
그러면 [2 7 1 4]에서 LIS를 구할 때 문제가 생긴다. 아래 흐름을 살펴보자.
- 원소가 2일 때 LIS는 초기값 1
- 원소가 7일 때 0 < 1이고 a0 = 2이다. 그리고 LIS(0)은 1이므로 LIS(1)은 2
- 원소가 1일 때 이를 만족하는 j가 없으므로 LIS는 2
- 원소가 4일 때 2 < 3이고 a2 = 1이다. 그리고 LIS(2)는 2므로 LIS(3)은 3
그럼 가장 긴 LIS는 3이라는 결과가 나오고, 이는 정답이 아니다.
따라서 1번 경우처럼 생각하면 안되고 무조건 2번 경우처럼 생각해야 한다.
이를 코드로 구현하면 아래와 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class LIS {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int[] LIS = new int[N];
int answer = 0;
for (int i = 0; i < N; i++) {
LIS[i] = 1;
for (int j = 0; j < i; j++) {
if (arr[j] < arr[i] && LIS[i] < LIS[j] + 1) {
LIS[i] = LIS[j] + 1;
}
}
if (answer < LIS[i]) {
answer = LIS[i];
}
}
System.out.println(answer);
}
}입력값은 아래와 같다.
6
3 2 6 4 5 1
출력 결과는 아래와 같다.
3
시간 복잡도는 O(N^2)이다.
최장 증가 수열의 길이를 이진 검색을 활용해 최적화할 수 있다.
위 DP의 시간 복잡도는 O(N^2)이다. 이를 이진 검색을 활용해 O(NlogN)까지 줄여보자.
방법은 아래와 같다.
- 배열을 순회한다.
- 배열 가장 뒤에 값을 추가할 수 있으면 추가한다.
- 배열 가장 뒤에 값을 추가할 수 없으면 값이 들어갈 수 있는 위치의 C 배열 값을 배열 값으로 바꿔준다.
자세한 건 아래 사진을 참고하자.
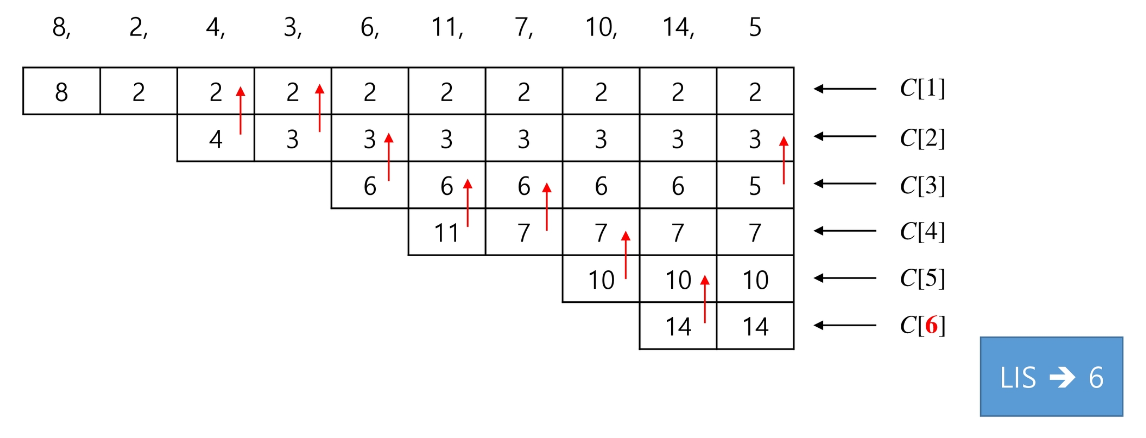
마지막에 나온 C 배열은 LIS의 크기만 보장하고, 해당 배열이 LIS 순서임을 보장하진 않는다.
이를 구현하면 아래와 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class LIS {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
List<Integer> LIS = new ArrayList<>();
for (int value : arr) {
boolean check = false;
for (int i = 0; i < LIS.size(); i++) {
if (value <= LIS.get(i)) {
LIS.set(i, value);
check = true;
break;
}
}
if (check == true) {
continue;
}
LIS.add(value);
}
System.out.println(LIS.size());
}
}입력값은 아래와 같다.
6
3 2 6 4 5 1
출력 결과는 아래와 같다.
3
