Algorithm 22일차

알고리즘에서 0-1 배낭 문제를 해결하는 데 DP를 활용할 수 있다.

배낭 문제의 정의는 아래와 같다

무게와 가치가 다양한 물건들이 있다.
이 때, 배낭에 담을 수 있는 무게가 정해진 상황에서 최대의 가치를 얻는 방법은 무엇인가?
(물건을 쪼개서 담을 순 없다.)

배낭 문제를 DP로 풀기 위한 몇 가지 정리를 수행해보자.

1. 주어진 조건은 물건, 물건의 무게, 물건의 가치, 배낭의 용량으로 총 4가지이다.
2. 물건과 물건의 무게는 부분 문제를 정의하는 데 반드시 필요하다.
   물건을 하나씩 배낭에 담는 것과 안 담는 것을 현재 배낭에 들어 있는 물건의 가치의 합에 근거하여 결정하기 때문이다.
3. 그리고 물건을 배낭에 담으려 할 땐 배낭 용량의 초과 여부를 검사해야 한다.

그래서 배낭 문제의 부분문제를 아래와 같이 정의할 수 있다.

그럼 i번째 물건을 담을지 안 담을지는 아래와 같다.

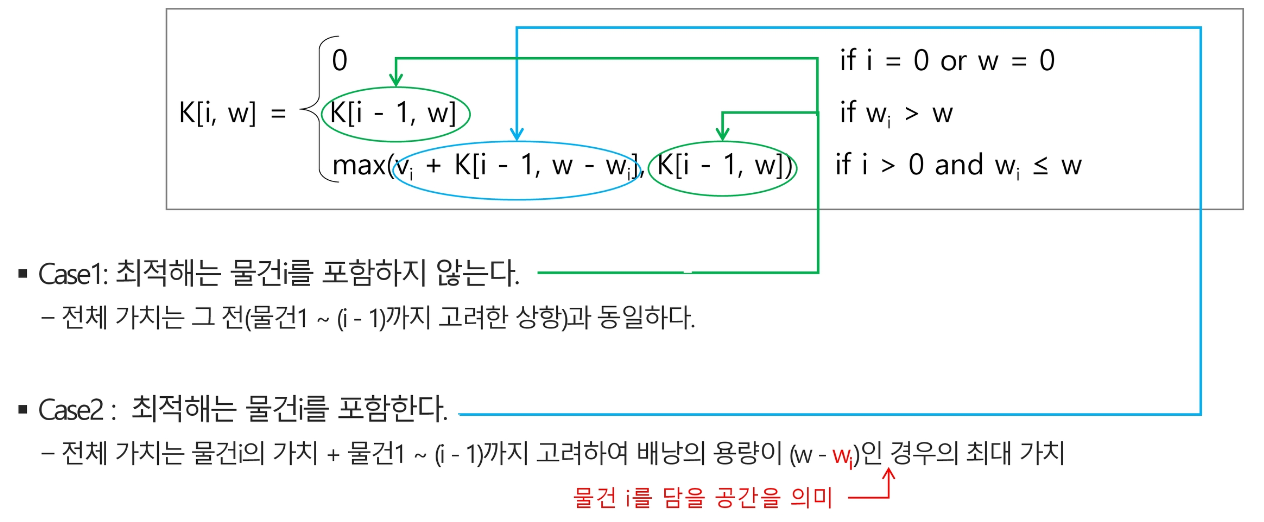
이를 코드로 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class KnapsackTest {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		int W = Integer.parseInt(br.readLine());
		
		int[] weights = new int[N+1];
		int[] profits = new int[W+1];
		
		for (int i = 1; i <= N; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			
			weights[i] = Integer.parseInt(st.nextToken());
			profits[i] = Integer.parseInt(st.nextToken());
		}
		
		int[][] D = new int[N+1][W+1]; // x가 weight, y가 물건
		
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= W; j++) {
				if (j < weights[i]) {
					D[i][j] = D[i-1][j];
				} else {
					D[i][j] = Math.max(D[i-1][j-weights[i]] + profits[i], D[i-1][j]);
				}
			}
		}
		
		System.out.println(D[N][W]);
	}
}

입력값은 아래와 같다.

4
10
5 10
4 40
6 30
3 50

출력 결과는 아래와 같다.

90