트리

노드들이 나뭇가지처럼 연결된 비선형 계층적 자료구조

그래프의 한 종류이다.

• 하나의 루트 노드와 0개 이상의 하위 트리
• 비선형 자료구조 : 데이터를 순차적으로 저장하지 않음
• 재귀적 자료구조 : 트리 내에 또 다른 트리가 있다.
• loop가 없는 연결 무방향 그래프
• 모든 자식 노드는 하나의 부모 노드만 갖는다.
• 노드가 n개인 트리는 항상 n-1개의 간선을 가진다.
  
  

관련 용어

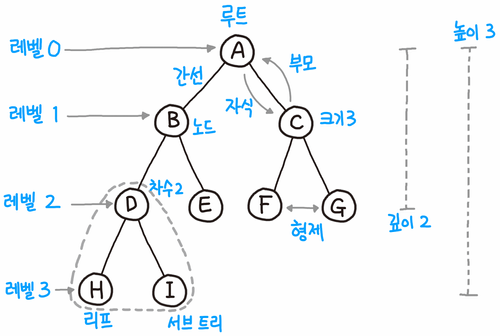
• 노드(Node) : 그래프의 정점
  • 루트 노드 : 트리의 기준이 되는 노드. 나무의 뿌리를 생각하면 된다. 루트 노드에서 가지가 뻗어나가는 이미지.
  • 부모 노드 : 자신과 인접한 노드들 중 루트 노드로 향하는 노드
  • 자식 노드 : 자신과 인접한 노드들 중 루트 노드의 반대 방향으로 향하는 노드
  • 단말 노드 : 자식 노드가 존재하지 않는 노드. 가지의 끝
  • 형제 노드 : 부모 노드가 같은 노드
• 가지(Branch) : 그래프의 간선. 트리에서는 양방향 간선만 사용한다.
• 부트리(Sub Tree) : 부분 그래프와 비슷하게 정의한다.
• 차수(Degree) : 자식 노드의 개수.
• 길이(Length) : 임의의 두 노드를 시작 노드, 도착 노드로 하는 경로에서 거치게 되는 노드의 수.
  • 깊이(Depth) : 루트 노드에서 해당 노드까지의 길이.
    • 레벨(Level) : 깊이가 같은 노드의 집합.
    • 높이(Height) : 가장 깊이가 깊은 단말 노드까지의 길이. 깊이 중 최댓값

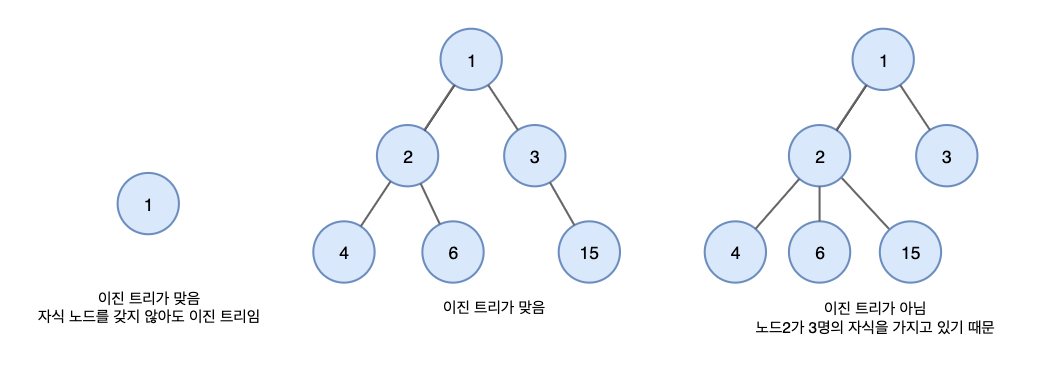
이진 트리(Binary Tree)

각 노드가 최대 두 개의 자식을 갖는 트리

구현

1. 배열로 구현 : 단순히 트리를 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 배열에 넣으면 된다.

/*       5
 *     /   \
 *    3      8
 *   / \   /  \
 *  1   4  7   9
 */
const tree = [null, 5, 3, 8, 1, 4, 7, 9];

2. 연결 리스트로 구현 : 연결리스트 구현 방식이랑 같음

function Node(val) {
  this.val = val;
  this.left = null;
  this.right = null;
}

let root = new Node(5);
let left = new Node(3);
let right = new Node(8);
root.left = left;
root.right = right;

이진 탐색 트리(Binary Search Tree)

모든 노드가 [ 모든 왼쪽 자식들 < n < 모든 오른쪽 자식들 ]의 특징을 가지는 이진 트리

같은 값을 가지는 노드는 없다.

관련 알고리즘

• 이진 트리 순회 알고리즘
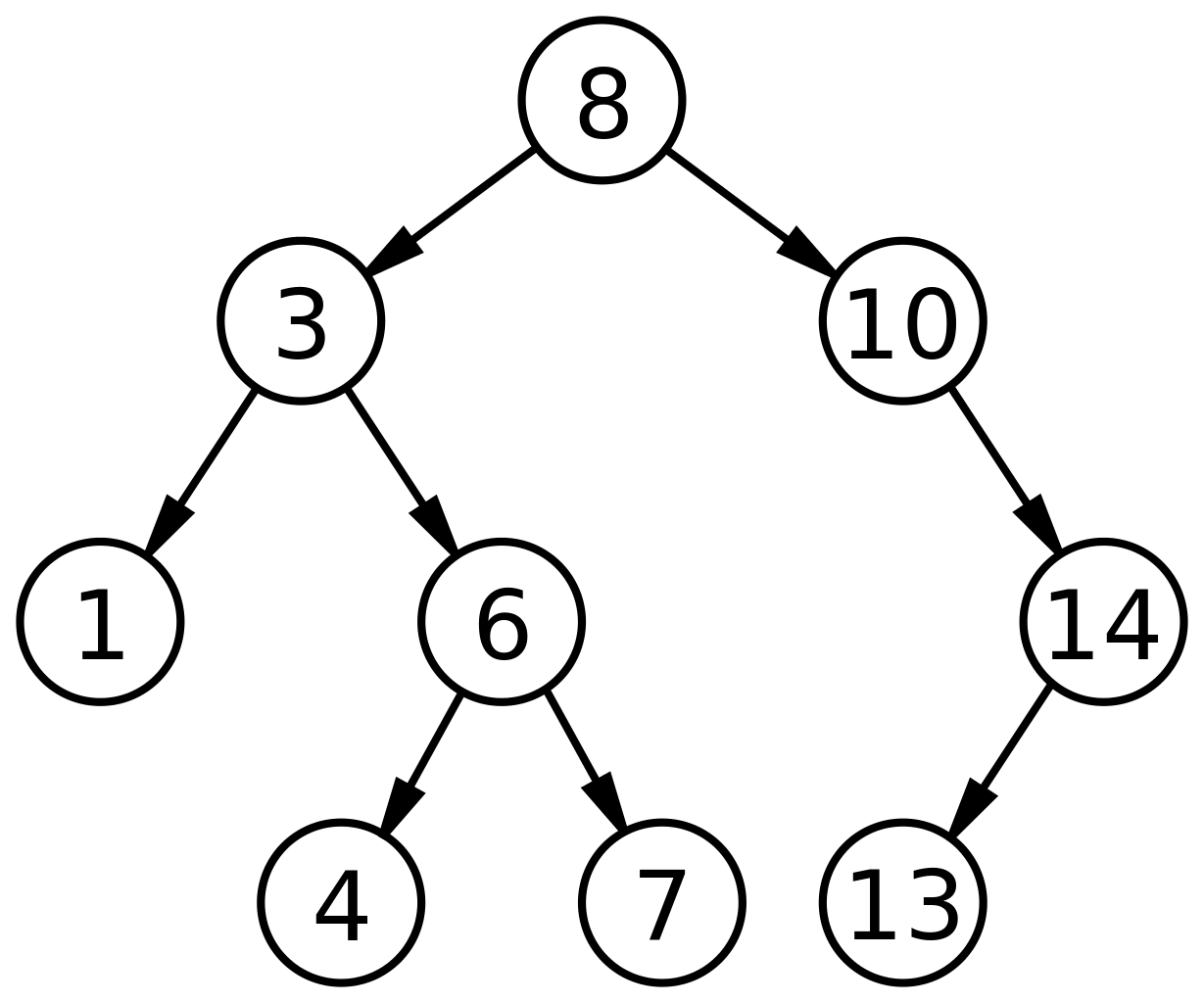
  • 전위 순회(preorder traverse) : 뿌리(root)를 먼저 방문
    • 뿌리 -> 왼쪽 자식 -> 오른쪽 자식( 8 -> 1 -> 3 -> 6 -> 4 -> 7 ....)
  • 중위 순회(inorder traverse) : 왼쪽 하위 트리를 방문 후 뿌리(root)를 방문
    • 왼쪽자식 -> 뿌리 -> 오른쪽 자식( 1 -> 3 -> 4 -> 6 -> 7 -> 8 -> ...)
  • 후위 순회(postorder traverse) : 하위 트리 모두 방문 후 뿌리(root)를 방문
    • 왼쪽자식-> 오른쪽 자식 -> 뿌리(1 -> 4 -> 7 -> 6 -> 3 -> 13 -> ..)
• 이진 탐색 알고리즘
  • 이진 탐색 트리일 때 탐색 알고리즘
  • 루트 노드부터 방문하여 찾는 값이 작으면 왼쪽, 크면 오른쪽을 방문하며 값을 찾는다.

이진트리 관련 자료

https://velog.io/@dlgosla/CS-자료구조-이진-트리-Binary-Tree-vzdhb2sp