[자료 구조]힙(Heap)

힙(Heap)이란?

완전 이진 트리를 기반으로한 자료구조 중 하나 → 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안됨

루트 노드에는 최댓값 혹은 최솟값이 위치하며, 각 노드의 값은 해당 노드의 자식 노드들의 값보다 크거나 작음

힙의 시간 복잡도는 일반적으로 O(log n) → 대용량의 데이터의 우선순위를 처리할 때 매우 유용

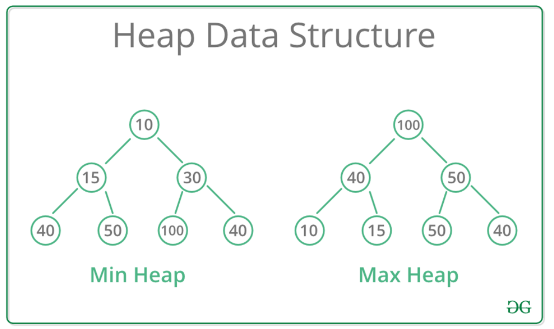
• 완전 이진 트리? : 루트 노드부터 왼쪽 자식 노드부터 차례로 채워져 있는 이진 트리를 의미

힙(Heap)의 종류

• 최대 힙(Max Heap)

  • 루트 노드에 최댓값이 위치하며, 각 노드들은 해당 노드의 자식 노드들의 값보다 크거나 같음
  • 우선순위 큐(Priority Queue)에서 최댓값을 반환하는 연산에 유용

• 최소 힙(Min Heap)

  • 루트 노드에 최솟값이 위치하며, 각 노드의 값은 해당 노드의 자식 노드들의 값보다 작거나 같음
  • 우선순위 큐에서 최솟값을 반환하는 연산에 유용

힙(Heap) 코드

PriorityQueue클래스를 사용하여 최소 힙을 구현 가능

• 최대 힙(Max Heap) 코드 예시

// 최대 힙(Max Heap) 코드 예시
import java.util.*;

class MaxHeap {
    private List<Integer> heap;
    
    public MaxHeap() {
        heap = new ArrayList<>();
    }
    
    private void heapifyUp(int index) {
        int parent = (index - 1) / 2;
        if (index > 0 && heap.get(index) > heap.get(parent)) {
            Collections.swap(heap, index, parent);
            heapifyUp(parent);
        }
    }
    
    private void heapifyDown(int index) {
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        int largest = index;
        if (left < heap.size() && heap.get(left) > heap.get(largest)) {
            largest = left;
        }
        if (right < heap.size() && heap.get(right) > heap.get(largest)) {
            largest = right;
        }
        if (largest != index) {
            Collections.swap(heap, index, largest);
            heapifyDown(largest);
        }
    }
    
    public void insert(int value) {
        heap.add(value);
        heapifyUp(heap.size() - 1);
    }
    
    public int extractMax() {
        int max = heap.get(0);
        heap.set(0, heap.get(heap.size() - 1));
        heap.remove(heap.size() - 1);
        heapifyDown(0);
        return max;
    }
}

• 최소힙 코드 예시

// 최소 힙(Min Heap) 코드 예시
import java.util.*;

class MinHeap {
    private List<Integer> heap;
    
    public MinHeap() {
        heap = new ArrayList<>();
    }
    
    private void heapifyUp(int index) {
        int parent = (index - 1) / 2;
        if (index > 0 && heap.get(index) < heap.get(parent)) {
            Collections.swap(heap, index, parent);
            heapifyUp(parent);
        }
    }
    
    private void heapifyDown(int index) {
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        int smallest = index;
        if (left < heap.size() && heap.get(left) < heap.get(smallest)) {
            smallest = left;
        }
        if (right < heap.size() && heap.get(right) < heap.get(smallest)) {
            smallest = right;
        }
        if (smallest != index) {
            Collections.swap(heap, index, smallest);
            heapifyDown(smallest);
        }
    }
    
    public void insert(int value) {
        heap.add(value);
        heapifyUp(heap.size() - 1);
    }
    
    public int extractMin() {
        int min = heap.get(0);
        heap.set(0, heap.get(heap.size() - 1));
        heap.remove(heap.size() - 1);
        heapifyDown(0);
        return min;
    }
}

참고
https://www.geeksforgeeks.org/heap-data-structure/
https://ko.wikipedia.org/wiki/힙(자료구조)