트리란?
노드(Node)들이 연결된 계층적인 구조를 가진 비순환적인 그래프
루트 누드가 있는데 이 노드를 제외하면 각 노드는 부모노드와 자식 노드를 가지는데, 각 노드들은 끊어진 연결이 없으며 다른 노드와 사이클을 이루지 않음
→ DB나 알고리즘이 자주 사용 됨
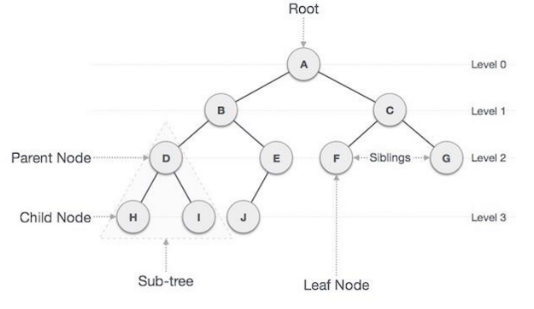
트리에서 사용되는 용어
- 루트 노드 : 트리의 가장 상위에 있는 노드. 다른 모든 노드는 루트 노드로부터 직.간접적으로 연결됨
- 부모 노드 : 자식 노드들을 가지고 있는 상위 노드. 여러개의 자식 노드를 가질 수 있음
- 자식 노드 : 부모 노드로부터 직접적으로 연결된 하위 노드.
- 잎 노드(Leaf Node),외부 노드(external node, outer node), 단말 노드 (terminal node) : 자식 노드가 없는 노드
- 깊이(Depth) : 루트 노드에서 해당 노드까지의 경로의 길이를 말함
- 높이(Height) : 해당 노드에서 잎 노드까지의 가장 긴 경로의 길이
- 간선 (Edge) : 노드와 노드 간의 연결선
- 내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node) : 자식 노드를 하나 이상 가진 노드
- degree : 노드의 자식의 수
트리의 종류
-
이진 트리(Binary Tree)
모든 노드가 최대 2개의 자식 노드를 갖는 트리
-
균형 트리(Balanced Tree)
트리의 모든 노드의 깊이 차이가 1 이하인 트리
-
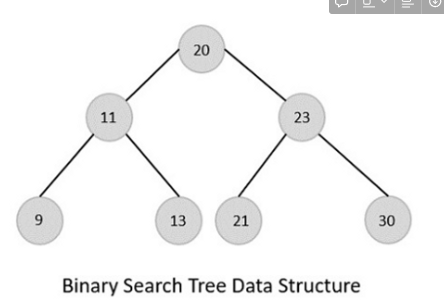
이진 탐색 트리(Binary Search Tree) BST
이진 트리의 한 종류로, 모든 노드가 아래 조건을 만족해야함
→ 왼쪽 자식 노드는 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드보다 크다.
class BinarySearchTree {
// 노드 클래스
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
Node root;
BinarySearchTree() {
root = null;
}
// 삽입 연산
void insert(int key) {
root = insertRec(root, key);
}
Node insertRec(Node root, int key) {
if (root == null) {
root = new Node(key);
return root;
}
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
return root;
}
// 탐색 연산
Node search(Node root, int key) {
if (root == null || root.key == key)
return root;
if (root.key > key)
return search(root.left, key);
return search(root.right, key);
}
// 삭제 연산
void delete(int key) {
root = deleteRec(root, key);
}
Node deleteRec(Node root, int key) {
if (root == null) return root;
if (key < root.key)
root.left = deleteRec(root.left, key);
else if (key > root.key)
root.right = deleteRec(root.right, key);
else {
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
root.key = minValue(root.right);
root.right = deleteRec(root.right, root.key);
}
return root;
}
int minValue(Node root) {
int minv = root.key;
while (root.left != null) {
minv = root.left.key;
root = root.left;
}
return minv;
}
// 중위 순회 연산
void inorder() {
inorderRec(root);
}
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.print(root.key + " ");
inorderRec(root.right);
}
}
}그래프(Graph)란?
노드와 간선(Edge)으로 구성된 자료구조
노드는 그래프에서 정점(Vertex)이라고도 부름
각 노드는 다른 노드와 연결된 간선을 가지며, 간선은 노드 사이의 관계를 나타냄.
→ 네트워크, 알고리즘, 인공지능 등 에서 사용됨
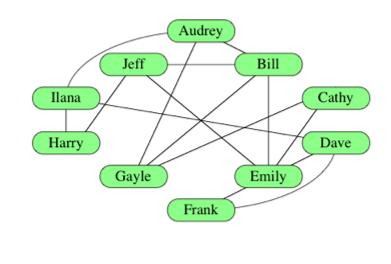
그래프에서 사용하는 용어
- vertices(정점) : 그래프에 있는 점들, 꼭지점
- Edges : 두 정점 사이의 경로
그래프의 종류
- 무향 그래프(Undirected Graph) 간선의 방향성이 없는 그래프를 의미 간선을 통해 양방향으로 이동 가능
- 유향 그래프(Directed Graph) 간선의 방향성이 있는 그래프 간선을 통해 한 방향으로만 이동 가능
[간선에 가중치 유무]
- 가중 그래프(Weighted Graph)
- 비가중 그래프(Unweighted Graph)
그래프 코드
import java.util.ArrayList;
import java.util.LinkedList;
public class GraphExample {
private ArrayList<Node> nodes;
public GraphExample() {
nodes = new ArrayList<>();
}
public void addNode(Node node) {
nodes.add(node);
}
public static class Node {
int value;
ArrayList<Node> neighbors;
public Node(int value) {
this.value = value;
neighbors = new ArrayList<>();
}
public void addNeighbor(Node neighbor) {
neighbors.add(neighbor);
}
}
public boolean hasPathDFS(Node source, Node destination) {
if (source == destination) {
return true;
}
for (Node neighbor : source.neighbors) {
if (hasPathDFS(neighbor, destination)) {
return true;
}
}
return false;
}
public boolean hasPathBFS(Node source, Node destination) {
LinkedList<Node> nextToVisit = new LinkedList<>();
boolean[] visited = new boolean[nodes.size()];
nextToVisit.add(source);
while (!nextToVisit.isEmpty()) {
Node node = nextToVisit.remove();
if (node == destination) {
return true;
}
if (visited[node.value]) {
continue;
}
visited[node.value] = true;
for (Node neighbor : node.neighbors) {
nextToVisit.add(neighbor);
}
}
return false;
}
public static void main(String[] args) {
GraphExample graph = new GraphExample();
Node node0 = new Node(0);
Node node1 = new Node(1);
Node node2 = new Node(2);
Node node3 = new Node(3);
node0.addNeighbor(node1);
node0.addNeighbor(node2);
node1.addNeighbor(node2);
node2.addNeighbor(node0);
node2.addNeighbor(node3);
node3.addNeighbor(node3);
graph.addNode(node0);
graph.addNode(node1);
graph.addNode(node2);
graph.addNode(node3);
System.out.println(graph.hasPathDFS(node0, node3)); // true
System.out.println(graph.hasPathBFS(node0, node3)); // true
}
}참고
(트리)
https://www.tutorialspoint.com/data_structures_algorithms/tree_data_structure.htm
https://docs.oracle.com/javase/8/docs/api/java/util/TreeMap.html
(그래프)
https://www.khanacademy.org/computing/computer-science/algorithms/graph-representation/a/describing-graphs
https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/
https://www.tutorialspoint.com/data_structures_algorithms/graph_data_structure.htm
