
선형 검색
정의
주어진 배열을 순차적으로 탐색하여 정해진 값을 검색하는 기법
말그대로 직선 모양으로 늘어선 배열에서 검색을 하고자 할 때, key value를 가진 원소를 찾을 때까지 맨 앞부터 하나씩 스캔하여 검색하는 알고리즘이다.
설명
설명

위와 같이 2, 4, 0, 1, 9로 이루어진 배열이 있고, 1이라는 숫자를 찾고자 한다.
이때 숫자, 즉 1이 내가 원하는 key value라고 볼 수 있다.
위 배열을 선형으로 검색하고자 할 때, 아래와 같은 과정을 거치게 된다.

알고리즘은 첫번째 값인 2를 키값인 1과 비교하게 되고, 다른 값이므로 다음으로 넘어간다.
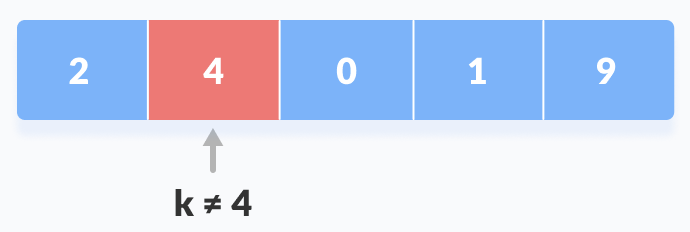
다음으로 알고리즘은 두번째 값인 4와 비교하게 되고, 역시 다음으로 넘어간다.
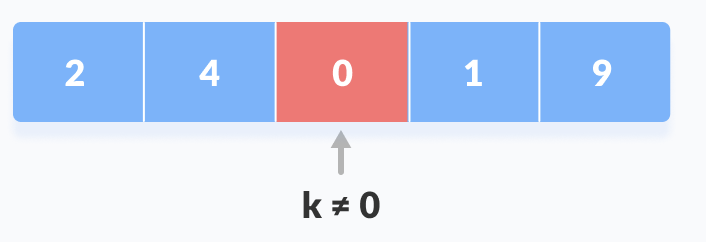
세번째 값인 0과 비교하고, 키 값인 1과 다르므로 다음 원소를 검색한다.
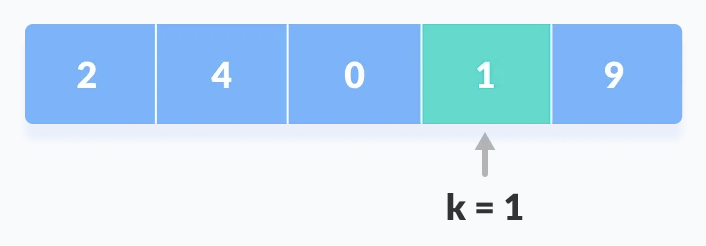
네번째 값인 1과 키 값인 1이 같으므로, 선형검색은 여기서 종료가 된다.
정리하자면 아래와 같이 될 것이다.
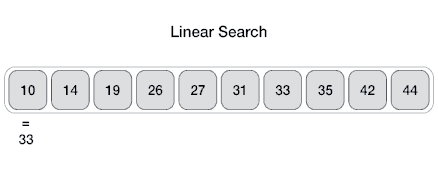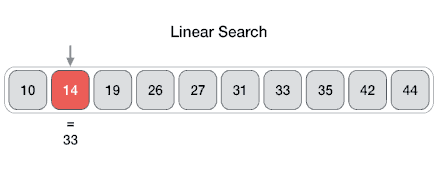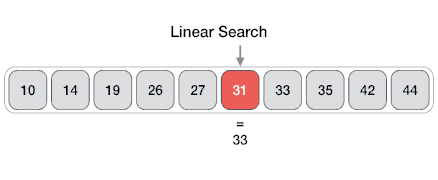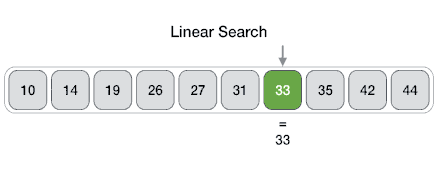
만약 배열에 키 값이 존재하지 않는다면?
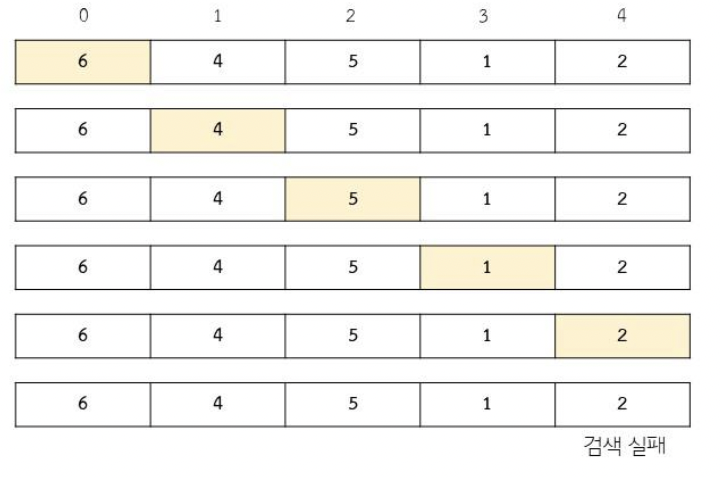
위 배열에서 3인 값을 찾고자 하는데 배열에 3이 존재하지 않는다면,
선형 검색 알고리즘은 배열을 끝까지 탐색할 것이고, 최종적으로는 검색 실패를 반환하게 될 것이다.
선형 검색 종료 조건
즉, 선형 검색이 종료되기 위해서는 아래 두가지 조건 중 하나가 충족되어야 한 다는 것을 알 수 있다.
1. 검색할 값을 찾지 못하고 배열의 맨 끝을 지나간 경우 - 검색 실패
2. 검색할 값과 같은 원소를 찾는 경우 -검색 성공
코드
기초 구현 코드
검색 종료 조건 두 개를 간단히 코드로 나타내보자면 다음과 같다.

a라는 임의의 배열(또는 시퀀스)에서 key 값을 찾고자 할 때 위와 같은 순서를 거치게 된다.
프로그램 구현
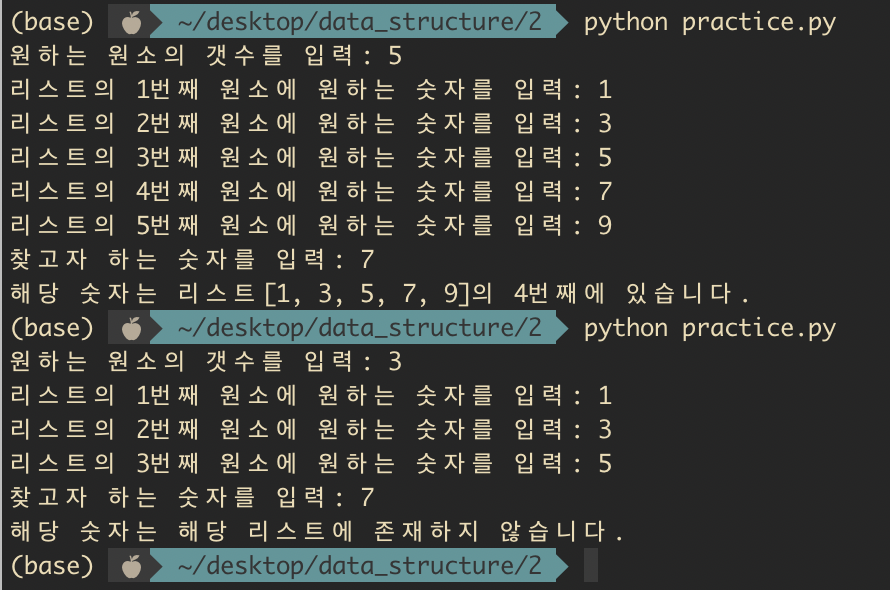
이제 위 로직을 이용한다면, 아래와 같이 배열과 원하는 키 값을 입력했을 때 배열의 순서를 정해주는 프로그램을 짤 수 있다.

이 프로그램을 구동해보면 아래와 같이 정상적으로 작동하는 것을 볼 수 있다.
for문 사용
for문을 사용해 주어진 배열을 순차대로 iterate하는 방식으로 선형 검색을 구현할 수도 있다.
이를 코드로 구현하자면 아래와 같다.

리스트의 i번째 원소가 key값과 같은 지를 비교하는 것인데, 위에 While문을 썼을 때보다 훨씬 간단하고 보기도 편하다.
프로그램 구현
위 로직을 통해 프로그램을 만들면 아래와 같이 나온다.

보초법 (Sentinel Method)
보초법의 필요성
위에서 선형 검색이 종료되기 위해서는 두가지 조건 중 하나가 충족되어야 한다고 했다.
1. 검색할 값을 찾지 못하고 배열의 맨 끝을 지나간 경우 - 검색 실패
2. 검색할 값과 같은 원소를 찾는 경우 -검색 성공
배열의 원소를 지날 때마다 알고리즘은 저 두개를 반복해서 체크를 해야한다.
1) 이 원소가 내가 찾고자 하는 키값과 같은지, 2) 틀리다면 지금 이 원소의 위치가 배열의 맨 끝인지
배열의 원소 갯수가 적다면 큰 차이가 없겠지만, 만약 그 수가 100억, 1000억개가 된다면 필요한 시간은 기하급수적으로 늘어날 수 밖에 없다.
이 두가지 탐색 조건을 하나로 줄여주는 것이 보초법이다.
정의
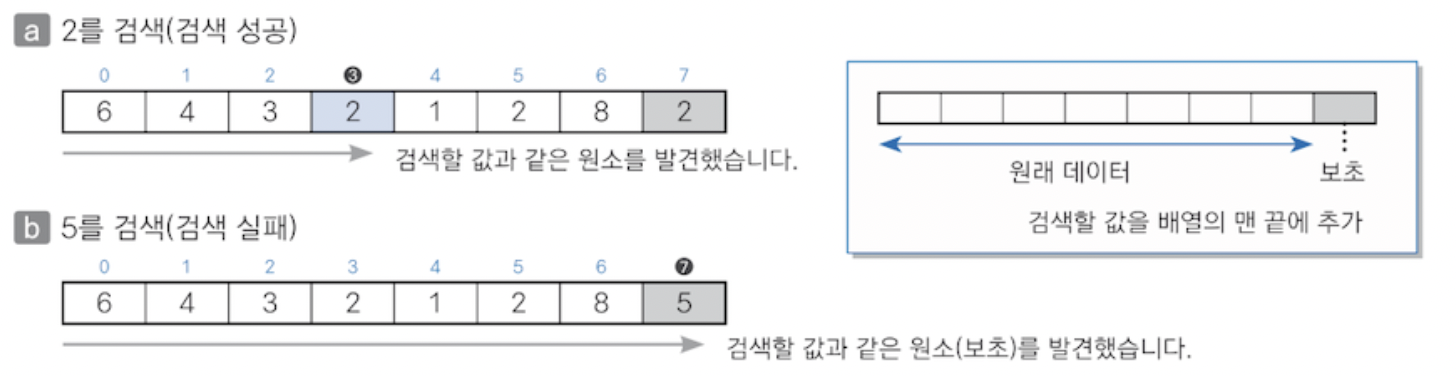
찾고자 하는 키 값을 배열의 맨 끝으로 보내는 것이 보초법이다.
이때 맨 끝에 저장된 키 값을 보초(sentinel)이라고 한다.
이렇게 된다면 위 선형검색의 종료 조건 중 1번인 검색 실패 조건, 검색할 값을 찾지 못하고 배열의 맨 끝을 지나간 경우를 제외할 수 있게 된다.
맨 끝을 지나기 전에 키값을 찾게 된다면 선형 검색이 성공하게 된 것이고, 맨 끝의 키값에서 일치하는 키값을 찾게 된다면 선형 검색이 실패한 것으로 간주하면 되기 때문이다.
코드
선형 검색을 구현할 수 있다면 보초법은 아주 쉽게 표현될 수 있다.
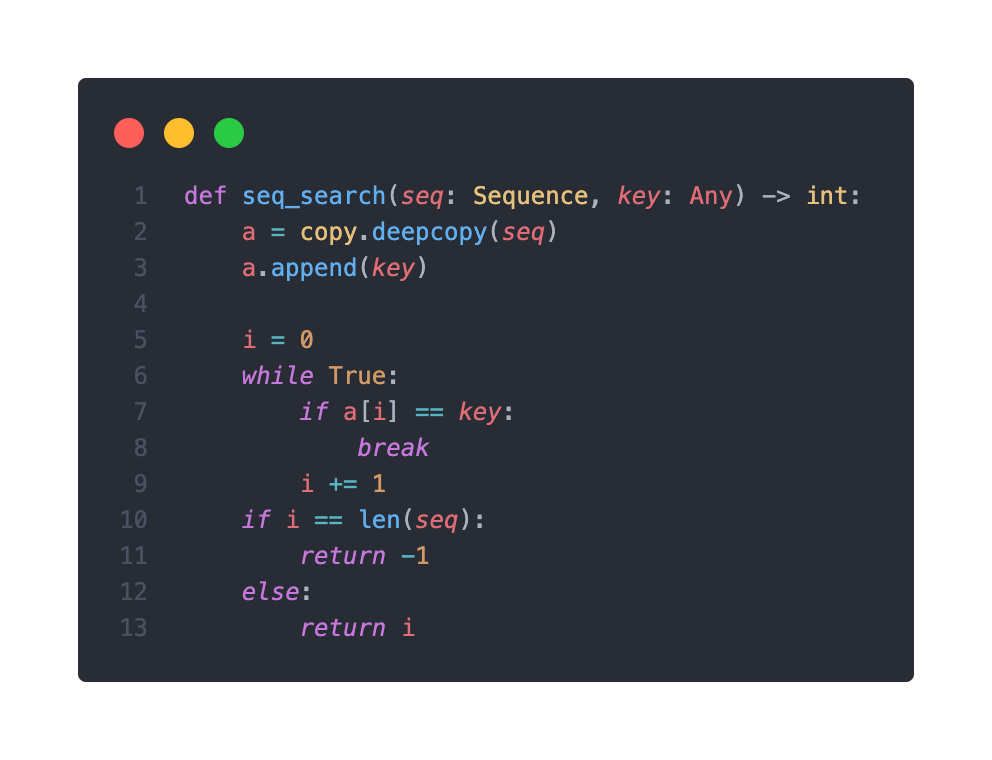
seq배열과 동일한a를 카피하여 생성하고, 배열a의 마지막에key값을 원소로 추가- 배열
a의i번째 요소가key값과 같아질때까지 찾고,i값을 반환 i값이seq의 길이와 같으면,seq에는key값이 없었다는 뜻이므로 검색 실패- 다른 경우엔
seq안에 있었다는 뜻이 되므로 검색 성공
참고
https://www.programiz.com/dsa/linear-search
https://yoongrammer.tistory.com/74#보초_법_(Sentinel_method)
