트리 Tree

Queue and stack are a linear data type.
Trees are non-linear.

Folders are a tree data type

Tree terms

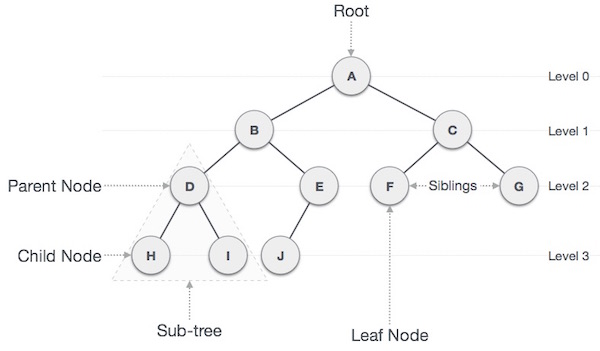
• Node: 트리에서 데이터를 저장하는 기본 요소
• Root Node: 트리 맨 위에 있는 노드
• Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
• Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
• Child Node: 어떤 노드의 하위 레벨에 연결된 노드
• Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
• Sibling: 동일한 Parent Node를 가진 노드
• Depth: 트리에서 Node가 가질 수 있는 최대 Level

Types of tree

이진 트리 Binary Tree

Every node has up to two child nodes.

      o      Level 0 
    o o o    Level 1
   o  o  o   Level 2 # 이진 트리(X)

      o      Level 0 
    o   o    Level 1
   o o o     Level 2 # 이진 트리(O)

완전 이진 트리 Complete Binary Tree

Every node has up to two child nodes and the child must be inserted from the leftmost node.

      o      Level 0
    o   o    Level 1
     o o     Level 2  # -> 이진 트리 O 완전 이진 트리 X

      o      Level 0
    o   o    Level 1
   o o o     Level 2  # -> 이진 트리 O 완전 이진 트리 O

Expressing a Complete Binary Tree in an array

The complete binary tree has rules that can allow it to be contained in an array.

The first index is None for convenience.

      8      Level 0 -> [None, 8] 첫번째 레벨의 8을 넣고,
    6   3    Level 1 -> [None, 8, 6, 3] 다음 레벨인 6, 3을 넣고
   4 2 5     Level 2 -> [None, 8, 6, 3, 4, 2, 5] 다음 레벨인 4, 2, 5를 넣으면 됩니다!

1. 현재 인덱스 * 2 -> 왼쪽 자식의 인덱스
2. 현재 인덱스 * 2 + 1 -> 오른쪽 자식의 인덱스
3. 현재 인덱스 // 2 -> 부모의 인덱스

Height of the Complete Binary Tree

The top (root) node is at level 0. Its children are level 1.

      o      Level 0  # 루트 노드
    o   o    Level 1
   o o o     Level 2  # 가장 아래 리프 노드

If there are 'k' number of nodes, then the maximum number of nodes that can exist is 2^k.

If the height is h:
Number of nodes N = 1 + 2^1 + 2^3 + 2^4 + ... + 2^h
Therefore, the maximum number of nodes that can exist is 2^(h+1)-1
2^(h+1)-1 = N -> h = log2(N+1)-1
Therefore its complexity is O(log(N))

힙 Heap

Heap is a complete binary tree to quickly find the max or min value.
Heap must have the max or min value in root.
This rule must be followed when adding or deleting a node.

Adding a node

The maximum height is O(log(N)) and therefore this function has a complexity of O(log(N)).
1. 원소를 맨 마지막에 넣습니다.
2. 그리고 부모 노드와 비교합니다. 만약 더 크다면 자리를 바꿉니다.
3. 부모 노드보다 작거나 가장 위에 도달하지 않을 때까지 2. 과정을 반복합니다.

이 맥스 힙에서 9를 추가해보겠습니다!
      8      Level 0
    6   3    Level 1  
   4 2 1     Level 2 

1. 맨 마지막에 원소를 넣습니다.

      8      Level 0
    6   3    Level 1  
   4 2 1 9   Level 2 

2-1. 부모 노드와 비교합니다. 3보다 9가 더 크니까! 둘의 자리를 변경합니다.

      8      Level 0
    6   3    Level 1  
   4 2 1 9   Level 2 

      8      Level 0
    6   9    Level 1  
   4 2 1 3   Level 2 

2-2. 다시 부모 노드와 비교합니다. 8보다 9가 더 크니까! 둘의 자리를 변경합니다.

      8      Level 0
    6   9    Level 1  
   4 2 1 3   Level 2 

      9      Level 0
    6   8    Level 1  
   4 2 1 3   Level 2 

3. 가장 위에 도달했으므로 멈춥니다. 힙의 특성을 그대로 유지해 데이터를 삽입했습니다!

      9      Level 0
    6   8    Level 1  
   4 2 1 3   Level 2

class MaxHeap:
    def __init__(self):
        self.items = [None]

    def insert(self, value):
        self.items.append(value)
        index = len(self.items) - 1
        
        # 값이 부모 값보다 크면 swap
        # 1층 비교했으면 while 반복문을 멈춤
        while index > 1:
            parentIndex = index // 2
            if value > self.items[parentIndex]:
                self.items[index], self.items[parentIndex] = self.items[index // 2], self.items[index] 
                index = parentIndex
            # 부모 값이 더 크면 break
            else:
                break
        return

Deleting a node

The maximum height is O(log(N)) and therefore this function has a complexity of O(log(N)).

1. 루트 노드와 맨 끝에 있는 원소를 교체한다.
2. 맨 뒤에 있는 원소를 (원래 루트 노드)를 삭제한다. (When deleting, the root node is always deleted.
3. 변경된 노드와 자식 노드들을 비교합니다. 두 자식 중 더 큰 자식과 비교해서 자신보다 자식이 더 크다면 자리를 바꿉니다.
4. 자식 노드 둘 보다 부모 노드가 크거나 가장 바닥에 도달하지 않을 때까지 3. 과정을 반복합니다.
5. 2에서 제거한 원래 루트 노드를 반환합니다.

이 맥스 힙에서 원소를 제거해보겠습니다! (항상 맨 위의 루트 노드가 제거 됩니다.)
      8      Level 0
    6   7    Level 1  
   2 5 4 3   Level 2 

1. 루트 노드와 맨 끝에 있는 원소를 교체한다.

      8      Level 0
    6   7    Level 1  
   2 5 4 3   Level 2 

      3      Level 0
    7   6    Level 1  
   2 5 4 8   Level 2 

2. 맨 뒤에 있는 원소를 (원래 루트 노드)를 삭제합니다. 
이 값이 기존 맥스힙에 있던 가장 큰 값입니다. 따라서 이 값을 마지막에는 반환해줘야 합니다!

      3      Level 0
    6   7    Level 1  
   2 5 4 X   Level 2 

3-1. 변경된 노드를 더 큰 자식 노드와 비교해야 합니다. 
우선 부모와 왼쪽 자식을 비교합니다. 그리고 부모와 오른쪽 자식을 비교합니다.
그리고 부모 보다 큰 자식 중, 더 큰 자식과 변경해야 합니다.
왼쪽 자식인 6과 오른쪽 자식인 7 중에서 7이 더 크고, 부모인 3보다 크니까 둘의 자리를 변경합니다.

      3      Level 0
    6   7    Level 1  
   2 5 4     Level 2 

      7      Level 0
    6   3    Level 1  
   2 5 4     Level 2 

3-2. 다시 자식 노드와 비교합니다. 
우선 부모와 왼쪽 자식을 비교합니다.
왼쪽 자식인 4는 부모인 3보다 더 크니까 둘의 자리를 변경합니다.

      7      Level 0
    6   3    Level 1  
   2 5 4     Level 2 

      7      Level 0
    6   4    Level 1  
   2 5 3     Level 2 


4. 가장 아래 레벨에 도달했으므로 멈춥니다. 힙의 특성을 그대로 유지해 데이터를 삭제했습니다!

      7      Level 0
    6   4    Level 1  
   2 5 3     Level 2 

5. 그리고, 아까 제거한 원래 루트 노드, 8을 반환하면 됩니다!

def delete(self):
        if self.items == [None]:
            return [None]
        
        # Swap root node with last node
        self.items[1], self.items[-1] = self.items[-1], self.items[1]

        # Delete former root node
        prevMax = self.items.pop(-1)

        # Reorganize (heapify) the heap from root to child nodes
        index = 1

        while index <= len(self.items)-1:
            leftChildIndex = index * 2
            rightChildIndex = index * 2 + 1
            maxIndex = index

            # If the value of the new is smaller than its left child's value
            if self.items[maxIndex] < self.items[leftChildIndex] and leftChildIndex <= len(self.items) -1:
                maxIndex = leftChildIndex
            
            # If the value of the new is smaller than its right child's value
            if self.items[maxIndex] < self.items[rightChildIndex] and rightChildIndex <= len(self.items) -1:
                maxIndex = rightChildIndex

            # If current index has the biggest value, break
            if maxIndex == index:
                break

            self.items[maxIndex], self.items[index] = self.items[index], self.items[maxIndex]

        return prevMax  # 8 을 반환해야 합니다.