그래프 Graph

A data structure that expresses the relationship between nodes.

• 노드(Node): 연결 관계를 가진 각 데이터를 의미합니다. 정점(Vertex)이라고도 합니다.
• 간선(Edge): 노드 간의 관계를 표시한 선.
• 인접 노드(Adjacent Node): 간선으로 직접 연결된 노드(또는 정점)

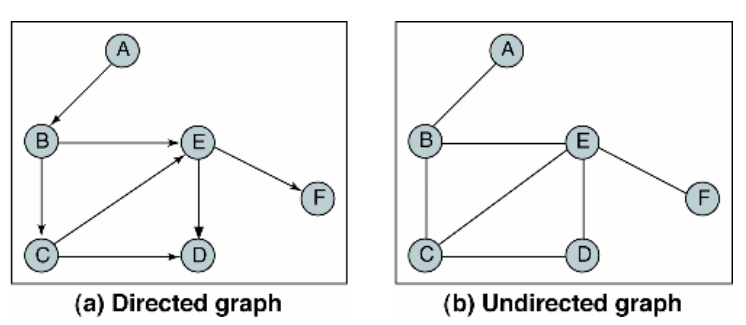
Types of graphs

• 유방향 그래프(Directed Graph): 방향이 있는 간선을 갖습니다. 간선은 단방향 관계를 나타내며, 각 간선은 한 방향으로만 진행할 수 있습니다.
• 무방향 그래프(Undirected Graph)는 방향이 없는 간선을 갖습니다

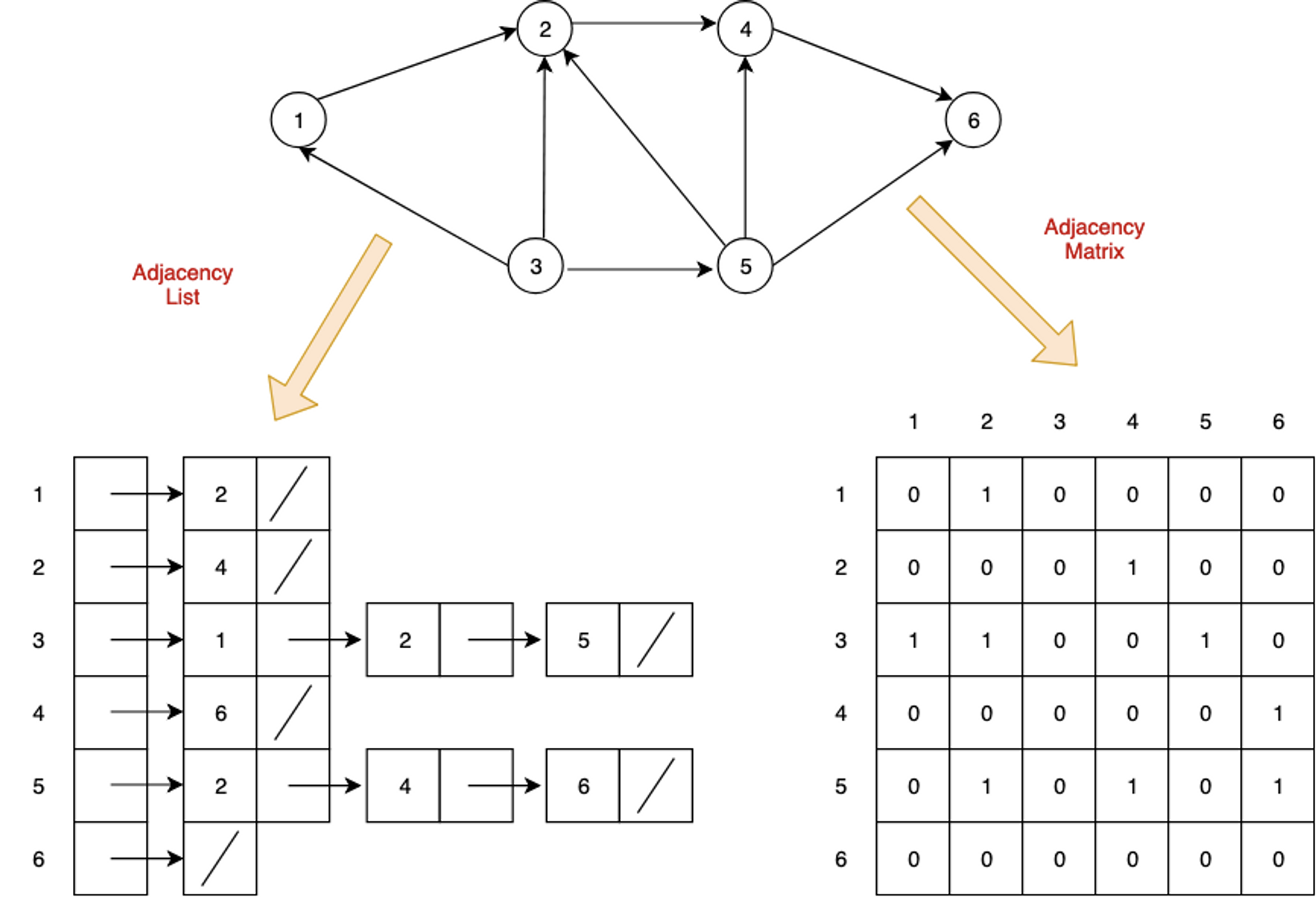
Expressing graphs

Two ways to express graphs:
1. 인접 행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관계를 표현
2. 인접 리스트(Adjacency List): 링크드 리스트로 그래프의 연결 관계를 표현

For example:

         2 - 3
          ⎜       
      0 - 1

Expressing this graph in an adjacency matrix:

  0  1  2  3
0 X  O  X  X
1 O  X  O  X
2 X  O  X  O
3 X  X  O  X

이걸 배열로 표현하면 다음과 같습니다!
graph = [
    [False, True, False, False],
    [True, False, True, False],
    [False, True, False, True],
    [False, False, True, False]
]

Expressing this in an adjacency list:

인접 리스트는 모든 노드에 연결된 노드에 대한 정보를 차례대로 다음과 같이 저장합니다.

0 -> 1
1 -> 0 -> 2
2 -> 1 -> 3
3 -> 2

이를 딕셔너리로 표현하면 다음과 같습니다!
graph = {
    0: [1],
    1: [0, 2]
    2: [1, 3]
    3: [2]
}

Difference between the adjacency matrix and list

Using one or the other uses either more space or time.

Complexity of adjacency matrix and list

	Adjacency matrix	Adjacency list
Space	O(N^2)	O(N+E)
Querying	O(1)	O(N)

Where E is the edge (간선).

The time complexity of the adjacency matrix to query is O(1) as you can call a node using matrix[i][j].
The time complexity of the adjacency list is at worst O(N) as you need to check every adjacent vertex.

The time complexity of the adjacency matrix to add a node is O(N^2) as the matrix has to increase by N+1, thus the complexity increasing by O((N+1)^2).
The time complexity of the adjacency list to add a node is O(1) as the pointer points to the front and rear node (like a linked list).

More about the difference in time complexity for other functions