Computational Thinking

논리

Hard Logic

• 직관적인 논리로 프로그래밍을 하면, 프로그램 동작 X
• 프로그래밍 언어의 표현들은, 모두 논리학의 기반
• 가정이 거짓이면 전체는 항상 참

Soft Logic

• 맥주집 문제를 풀 때는 직관을 사용
• 직관은 논리적인 느낌을 주는 것
• 익숙한 상황에서는 빠르지만 강한 착각을 일으킨다
• 일상 생활에서는 유리

증명

• 증명은 정확한 명제식으로 표현할 수 있는 것
• 보통은 정확한 명제식까지 쓰지는 않으나 근본벅으로 명제식으로 바꿀수 있음

수학적 귀납법 증명

• 수학적 귀납법의 기본형 : P(1)이 참이고, P(n) -> P(n+1)이 참이면 P(n)은 모든 자연수 n에 대해서 참이다.
• 수학적 귀납법의 강한 형태: P(1)이 참이고, P(1)^P(2)^....^P(n) -> P(n)이 참이면 P(n)은 모든 자연수 n에 대해서 참이다.

논리 연산자

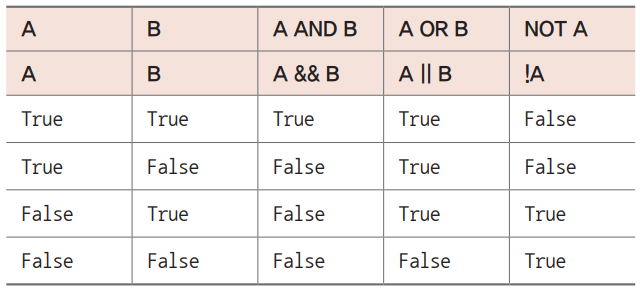
• 항진명제 : 진릿값이 항상 참
• 모순명제 : 진릿값이 항상 거짓
• 사건명제 : 항진명제도 모순 명제도 아닌 명제
• 조건명제
  • p,q과 명제일 때, 명제 p가 조건, q가 결론로 제시되는 명제
  • p -> q