SW 문제 해결 응용

부분집합

• 집합에 포함된 원소들을 선택하는 것

• Example) {A,B,C}

  {A,B,C}
  {}
  {A}
  {B}
  {A,B}
  {C}
  {A,C}
  {B,C}
  {A,B,C}

• 집합에서 부분집합 구현 방법

  • 1. 완전탐색
    • 재귀호출을 이용한 완전탐색으로, 부분집합을 구할 수 있다.
  • 2. Binary Counting
    • 2진수 & 비트연산을 이용하여, 부분 집합을 구할 수 있다.
    • 부분 집합이 필요할 때 사용하는 추천 방법

• 완전탐색

    arr = ['O', 'X']
    path = []
  
    def run(lev):
        if lev == 3:
            print(path)
            return
        for i in range(2):
            path.append(arr[i])
            run(lev+1)
            path.pop()
    run(0)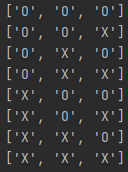

  

• Bianry Counting

  • 001 -> {A}

  • 110 -> {B,C}

     arr = ['A', 'B', 'C']
     n = len(arr)
    
     def get_sub(tar):
         for i in range(n):
             if tar & 0x1:
                 print(arr[i], end = '')
             tar >>= 1
    
     for tar in range(0, 1 << n): # range(0, 8)
         print('{', end = '')
         get_sub(tar)
         print('}')

조합

• 서로 다른 n개의 원소 중 r개를 순서 없이 골라낸 것
• 순열과 조합의 차이
  • 조합에서는 A B C와 C B A가 같은 경우이다.

## Case 1
arr = ['A', 'B', 'C', 'D', 'E']

for a in range(5):
    start1 = a + 1
    for b in range(start1, 5):
        start2 = b + 1
        for c in range(start2, 5):
            print(arr[a], arr[b], arr[c])

## Case 2
path = []
n = 3
def run(lev, start):
    if lev == n:
        print(path)
        return
    for i in range(start, 5):
        path.append(arr[i])
        run(lev + 1, i + 1)
        path.pop()
run(0, 0)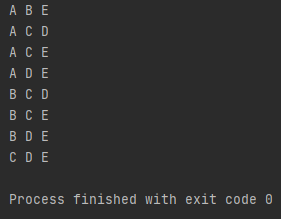

Greedy

Greedy 란?

• 결정이 필요할 때, 현재 기준으로 가장 좋아 보이는 선택지로 결정하여 답을 도축

• 동전 교환 문제

  • 가장 큰 가격부터 바꿔주기

    def solution(money):
     answer = 0
     change = [500, 100, 50, 10]
     remain = money
     for i in change:
         answer += remain // i
         remain = remain % i
     return answer

• Fractional Knaspack

  • 물건을 원하는 만큼 자르는 문제

  • Kg당 가격이 가장 높은 물건을 최대한 담는다

      n = 3
     target = 30
     things = [(5, 50), (10, 60), (20, 140)]
    
     things.sort(key = lambda x:(x[1] / x[0]), reverse=True)
    
     sum = 0
     for kg, price in things:
         per_price = price / kg
    
         if target < kg:
             sum += target * per_price
             break
         sum += price
         target -= kg
     print(int(sum))