SW 문제 해결 응용

반복(Iteration)과 재귀(Recursion)

• 반복과 재귀는 유사한 작업을 수행할 수 있다.

• 수행하는 작업이 완료될 때 까지 계속 반복

  • 루프 (for, while)
  • 반복문은 코드를 n번 반복시킬 수 있다.

• 재귀는 주어진 문제의 해를 구하기 위해 동일하면서 더 작은 문제의 해를 이용하는 방법

  • 하나의 큰 문제를 해결할 수 있는 더 작은 문제로 쪼개고 결과들을 결합
  • 재귀호출은 n 중 반복문을 만들어 낼 수 있다.

  for i in range(1,4):
      for j in range(1,4):
          print(f'{i}{j}')
  
  # 11
  # 12
  # 13
  # 21
  # 22
  # 23
  # 31
  # 32
  # 33

• 반복문으로는 n번 반복을 구현가능하고 재귀호출로 n중 for문 구현 가능

path = []
N = 3
def run(lev):
	if lev == N:
    	print(path)
        return
    for i in range(1, 4):
    	path.append(i)
        run(lev+1)
        path.pop()
run(0)

• 함수는 값만 복사가 되는 것이다.

def KFC(x):
    print(x)
    x += 1
    print(x)
    
x = 3
KFC(x+1)
print(x)

# 밑의 순서대로 출력 된다
# 4
# 5
# 3

• 재귀는 해당 함수를 호출했던 것으로 돌아온다

def BBQ(x):
    x += 10
    print(x)
    
def KFC(x):
    print(x)
    x += 3
    BBQ(x + 2)
    print(x)
    
x = 3
KFC(x + 1)
print(x)

# 4
# 19
# 7
# 3

# 0 1 2 3 4 5 4 3 2 1 0

def recur1(x):
    if x == 5:
        recur2(x)
        return
    print(x, end = " ")
    x += 1
    recur1(x)

def recur2(x):
    if x < 0:
        return
    print(x, end = " ")
    x -= 1
    recur2(x)
recur1(0)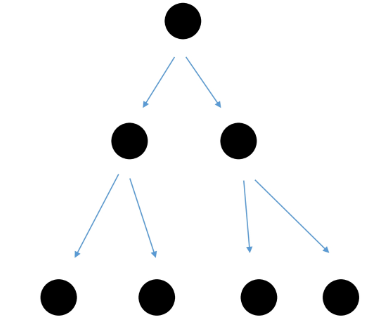

def recur(x):
    if x == 2:
        return
    recur(x+1)
    recur(x+1)
    print(x)
    
recur(0)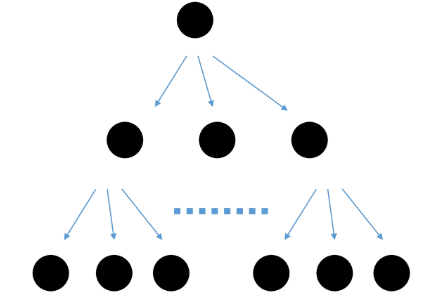

def recur(x):
    if x == 2:
        return
    recur(x+1)
    recur(x+1)
    recur(x+1)
    print(x)
    
recur(0)

# Depth 3, 재귀 호출 4
def recur(x):
    if x == 3:
        return
    recur(x + 1)
    recur(x + 1)
    recur(x + 1)
    recur(x + 1)

recur(0)

# Depth 3, 재귀 호출 4
def recur(x):
    if x == 3:
        return
    for i in range(4):
        recur(x + 1)

recur(0)

순열

순열이란?

• 서로 다른 N개에서 R개를 중복없이, 순서를 고려하여 나열 (중복 허용 X)

중복순열?

• 서로 다른 N개에서 R개를 중복 허용하고, 순서 나열

path = []
def recur(x):
    if x == 3:
        print(*path)
        return
    for _ in range(1,7):
        path.append(_)
        recur(x+1)
        path.pop()

recur(0)

# 1 1 1
# 1 1 2
# 1 1 3
# 1 1 4
# 1 1 5
# 1 1 6
# 1 2 1
# 1 2 2
# 1 2 3
# 1 2 4
# ...
# 6 6 3
# 6 6 4
# 6 6 5
# 6 6 6

중복을 취급하지 않는 순열 구현 방법

• 중복 순열 코드 작성 후 중복을 제거하는 코드 추가
• 제거 원리
  • 전역 리스트를 사용하면 이미 선택한 숫자 구별 가능

#### CASE 1
path = []
used = [False, False, False, False, False, False, False]
def recur(x):
    if x == 3:
        print(*path)
        return
    for _ in range(1, 7):
        if used[_] == True : continue
        used[_] = True
        path.append(_)
        recur(x+1)
        path.pop()
        used[_] = False        

recur(0)


#### CASE 2
path = []
def recur(x):
    if x == 3:
        print(*path)
        return
    for _ in range(1,7):
        if _ not in path:
            path.append(_)
            recur(x+1)
            path.pop()

recur(0)
# 1 2 3
# 1 2 4
# 1 2 5
# 1 2 6
# 1 3 2
# 1 3 4
# 1 3 5
# 1 3 6
# 1 4 2
# 1 4 3
# ...
# 6 5 1
# 6 5 2
# 6 5 3
# 6 5 4

# 주사위

path = []
def recur(x):
    if x == 2:
        print(*path)
        return
    for _ in range(1,7):
        path.append(_)
        recur(x + 1)
        path.pop()
recur(0)
# 1 1
# 1 2
# 1 3
# 1 4
# 1 5
# 1 6
# 2 1
# ...
# 6 3
# 6 4
# 6 5
# 6 6

완전탐색

완전탐색

• 모든 가능한 경우를 모두 시도를 해보아, 정답을 찾아내는 알고리즘
• Example) 자전거 열쇠 비번
  • 1111 ~ 9999 : 4중 for문 시도
  • 1 ~ 9 까지 이뤄진 N자리 숫자 : 재귀호출