[정렬] 정렬 종류와 시간 복잡도

source: https://danidani-de.tistory.com/45

source: https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

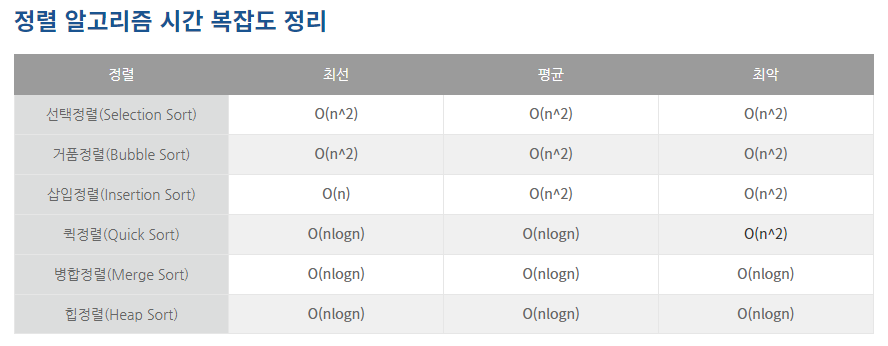
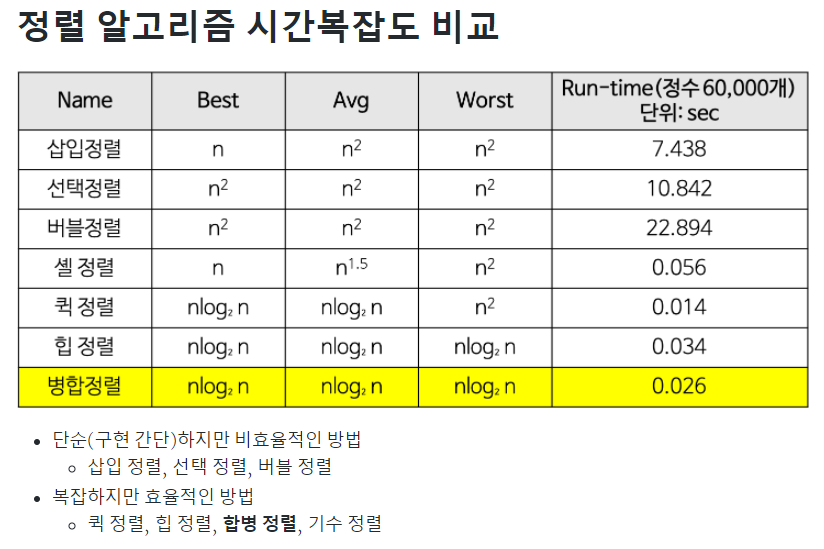
버블 정렬(Bubble Sort)

시간 복잡도: O(N^2), 메모리: O(1)

버블 정렬은 배열의 첫 원소부터 순차적으로 진행하며, 현재 원소가 그 다음 원소의 값보다 크면 두 원소를 바꾸는 작업을 반복한다. 이런식으로 배열을 계속 살펴보면서 완전히 정렬된 상태가 될 때까지 반복한다.

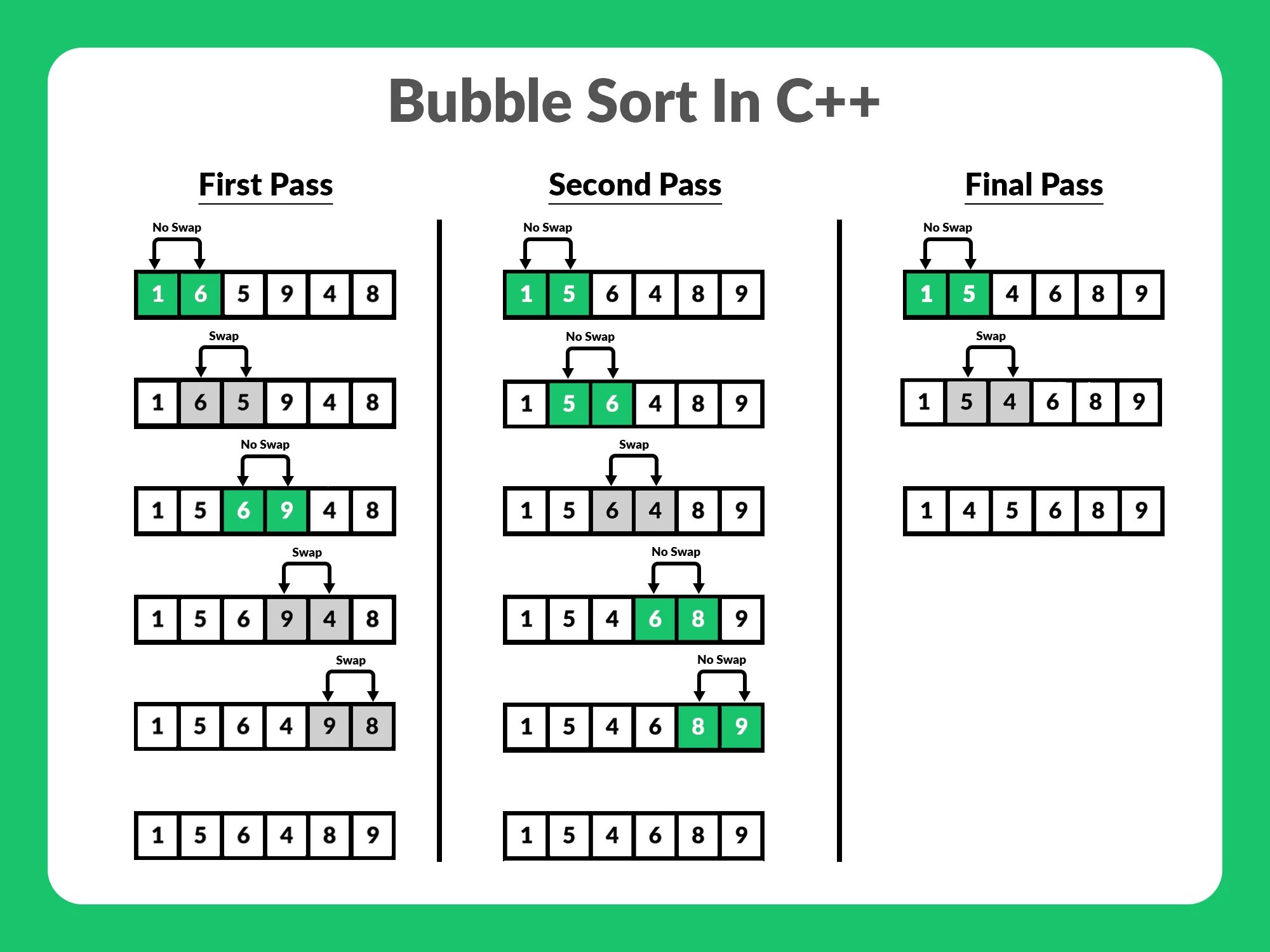
source: https://velog.io/@chayezo/Bubble-Sort-%EB%B2%84%EB%B8%94-%EC%A0%95%EB%A0%AC

1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 원소까지는 정렬에서 제외된다.
이렇게 1회전을 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.

소스코드

// 정렬할 벡터 vec

int len = vec.size();

for(int i=0; i<len; i++){
    for(int j=0; j<len-1-i; j++){
        if(vec[j] > a[j+1]){
            int temp = a[j];
            a[j] = a[j+1];
            a[j+1] = temp;
        }
    }
}

시간 복잡도

(n-1)(회전1) + (n-2)(회전2) + (n-3) + .. + 2 + 1 => n(n-1)/2 이므로 O(n^2)로 동일

공간 복잡도

주어진 배열 안에서 교환을 하므로(동적으로 메모리를 추가할 필요 없음) O(n)이다.

공간 복잡도
프로그램을 실행 및 완료하는데 필요한 저장공간의 양을 뜻함. 고정 공간 + 가변 공간

• 고정 공간: 알고리즘과 무관한 공간. 코드 저장 공간, 단순 변수 및 상수
• 가변 공간: 알고리즘 실행과 관련있는 공간. 실행 중 동적으로 필요한 공간

---

선택 정렬(Selection Sort)

시간 복잡도: O(n^2), 메모리: O(1)

선택 정렬은 가장한 심플한 알고리즘이다. 하지만 비효율적이다. 배열을 선형 탐색(linear scan)하며 가장 작은 원소를 배열 맨 앞의 원소와 교체한다. 그 다음 두 번째로 작은 원소를 찾아 다시 앞으로 보낸다. 이 작업을 모든 원소가 정렬될 때까지 반복한다.

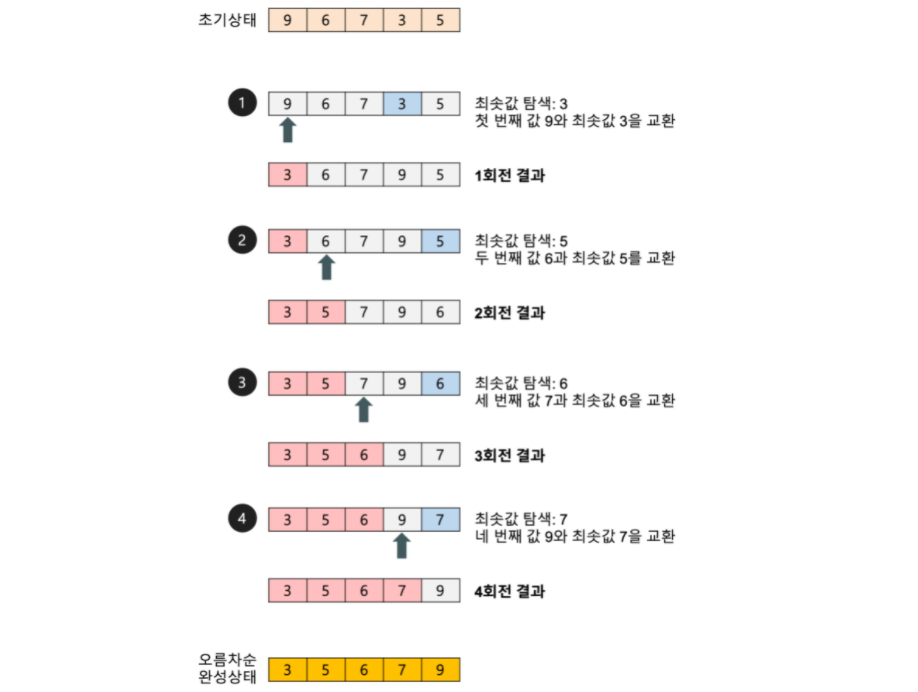
회전시마다 앞쪽 요소들은 정렬된 상태가 된다.

vector<int> selectionSort(vector<int> vec){
    int lastIdx = vec.size()-1;
    
    // O(n-1)
    for(int i=0; i<lastIdx; i++){   // lastIdx 제외 (n-1 루프) 
        int nowIdx = i;

        int minNum = vec[nowIdx];
        int minIdx = nowIdx;

        // O(K)
        for(int j= nowIdx+1; j <= lastIdx; j++){
            int nextIdx = j;
            if(vec[nextIdx] < minNum){
                minNum = vec[nextIdx];
                minIdx = nextIdx;
            }
        }

        // swap
        int temp = vec[nowIdx];
        vec[nowIdx] = minNum;
        vec[minIdx] = temp;
    }
    // =>  total: 약 O(N^2)
    return vec;
}

시간 복잡도

(n-1)(회전1) + (n-2)(회전2) + (n-3) + .. + 2 + 1 => n(n-1)/2 이므로 O(n^2)로 동일

공간 복잡도

주어진 배열 안에서 교환을 하므로(동적으로 메모리를 추가할 필요 없음) O(n)이다.

버블 정렬과 마찬가지로 알고리즘이 단순하다. 또한 마찬가지로 정렬하고자 하는 배열 안에서 교환하는 방식으로 다른 메모리 공간을 필요로 하지 않는다. (제자리 정렬(in-place sorting))
하지만 버블 정렬에 비해 실제로 교환하는 횟수는 적다.

---

삽입 정렬(Insertion Sort)

삽입 정렬 또한 시간 복잡도는 O(n^2)이다. 다만 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작!!
최선의 경우: O(n)
최악의 경우: O(n^2)
메모리: O(1)


보통의 경우 삽입 정렬보다 퀵 정렬이 효율적이나 정렬이 거의 되어 있는 상황에서는 퀵 정렬 알고리즘보다 더 강력.

vector<int> insertionSort(vector<int> vec){

    for(int i=1; i<vec.size(); i++){
        int nowIdx = i;

        for(int j=i; j>0; j--){
            // 이전 값과 비교
            if(vec[j] < vec[j-1]){
                // swap
                int temp = vec[j];
                vec[j] = vec[j-1];
                vec[j-1] = temp;
            }
        }
    }

    return vec;
}

시간 복잡도

(n-1)(회전1) + (n-2)(회전2) + (n-3) + .. + 2 + 1 => n(n-1)/2 이므로 O(n^2)로 동일.
하지만 거의 정렬이 되어있는 최적의 경우, 한번씩 밖에 비교를 안하므로 **O(n)에 가까운 시간 복잡도를 가진다.
또한 이미 정렬되어 있는 배열에 자료를 하나씩 삽입/제거하는 경우에는, 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다.

따라서 최선의 경우 O(n)의 시간 복잡도를 갖고, 평균과 최악의 경우 O(n^2)의 시간 복잡도를 갖게 된다.

공간 복잡도

주어진 배열 안에서 교환을 하므로(동적으로 메모리를 추가할 필요 없음) O(n)이다.

---

병합 정렬(merge sort)

시간 복잡도: O(NLogN), 메모리 상황에 따라 다름

(나누기)
병합 정렬은 배열을 절반씩 나누어 각각을 정렬한 다음 이 둘을 합하여 다시 정렬하는 방법. 나눈 절반을 정렬할 때도 같은 알고리즘이 사용되고 결국에는 원소 한개짜리 배열 두 개를 병합하게 된다.
(병합)
병합 작업을 수행하는 메서드는 병합 대상이 되는 배열의 두 부분을 임시배열에 복사하고, 왼쪽 절반의 시작지점, 오른쪽 절반의 시작 지점을 추적한다. 이 임시배열을 순회하면서 두 배열에서 더 작은 값의 원소를 꺼내어 원래 배열에 복사해 넣는다. 두 배열 중 한 배열에 대한 순회가 끝난 경우에는 다른 배열의 남은 부분을 원래 배열에 남김없이 복사해 넣고 작업을 마친다.

source: https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

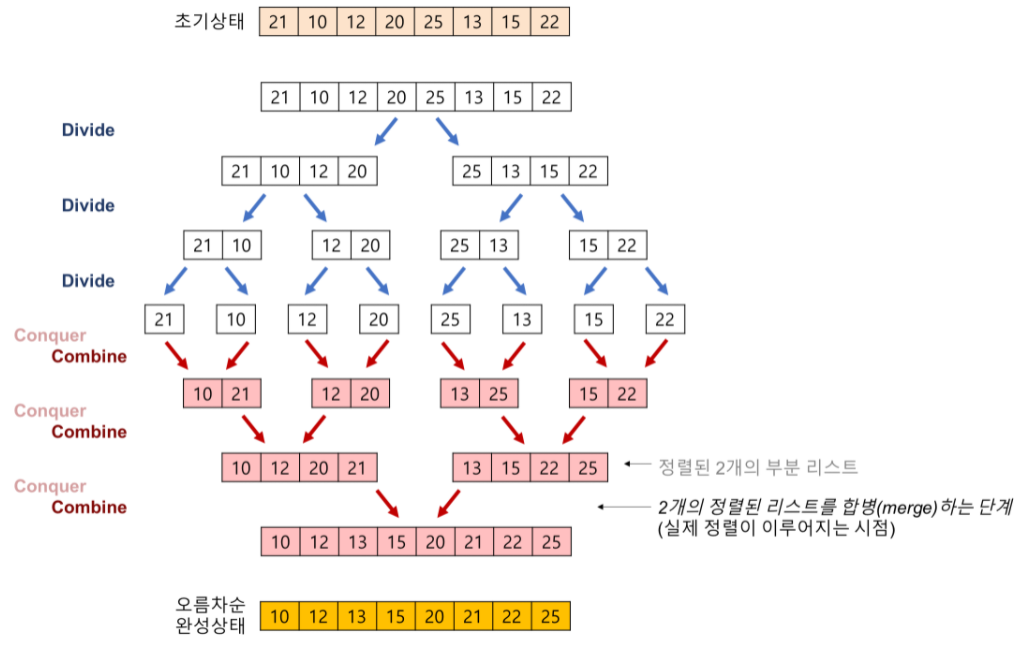
// conquer(정복) + combine(결합)
// => 부분 정렬
template<T>
vector<T> merge(vector<T>& arr1, vector<T>& arr2){
    
    // 병합된 결과가 저장될 벡터
    vector<T> merged;
    
    auto iter1 = arr1.begin();
    auto iter2 = arr2.begin();
    
    while(iter1 != arr1.end() && iter2 != arr2.end()){
        if(*iter1 < *iter2){
            merged.push_back(*iter1);
            iter1++;    // 반복자 이동
        }
        else{
            merged.push_back(*iter2);
            iter2++;
        }
    }
    
    if(iter1 != arr1.end()){
        for(; iter1 != arr1.end(); iter1++)
            merged.push_back(*iter1);
    }
    else{
        for(; iter2 != arr2.end(); iter2++)
            merged.push_back(*iter2);
    }

    // 정렬되어 병합된 벡터 리턴
    return merged;
}

// (total) divide + merge(함수)
// 병합 정렬
template<typename T>
vector<T> merge_sort(vector<T> arr){
    if(arr.size() > 1){
        // divide
        auto mid = size_t(arr.size() / 2);

        auto left_half = merge_sort<T>(vector<T>(arr.begin(), arr.begin()+mid));
        auto right_half = merge_sort<T>(vector<T>(arr.begin()+mid, arr.end()));

        // conquer + combine
        return merge<T>(left_half, right_half);
    }

    return arr;
}

시간 복잡도

=> O(NlogN)

공간 복잡도

임시 배열이나 벡터가 필요하다. 즉 제자리 정렬(in-place sorting)이 아니란 뜻이다.

=> O(2n)

합병 정렬 with 연결 리스트(linked list)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다. => 제자리 정렬로 구현 가능.

---

퀵 정렬(Quick Sort)

퀵 정렬은 무작위로 선정된 한 원소(pivot 역할)을 사용하여 배열을 분할.
선정된 원소보다 작은 원소들은 앞에, 큰 원소들은 뒤에 보낸다. => 그리고 배열이 분할된다.
배열 분할 작업은 위와같이 연속된 스왑(swap) 연산을 통해 효율적으로 수행된다.
배열과 그 부분 배열을 반복적으로 분할해 나가면 결국에 배열은 정렬된 상태에 도달한다.

하나의 분할 과정에서 사용되는 원소(pivot)이 중간값, 적어도 중간값에 가까운 값이 되리라는 보장이 없기에 퀵 정렬은 최악의 경우 수행 시간이 O(n^2)이 될 수 있다. 평균적으로는 O(N*LogN)이다.

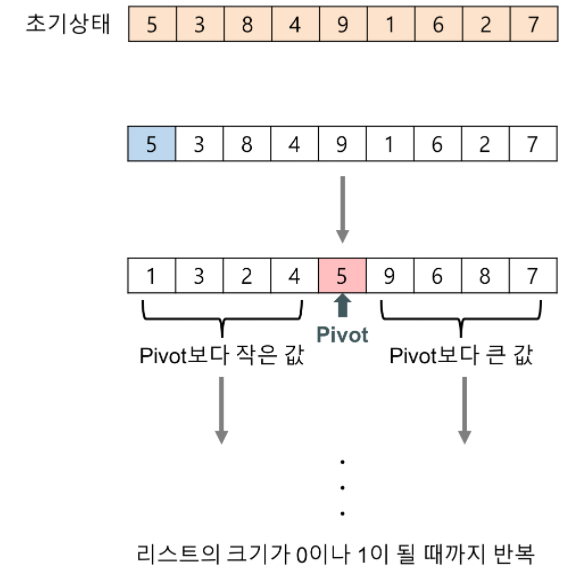
source: https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html

void quickSort(vector<int>& vec, int start, int end) {
	// 퀵정렬은 재귀 방식
	// 종료조건 필요
	if (start >= end)
		return;

	// (1) 피벗, left/right 인덱스 지정
	int pivot = start;	// 피벗을 첫번째 원소로 지정하는 경우
	int left = start + 1;
	int right = end;

	while (left <= right) {
		// 피벗보다 큰 데이터를 찾을 때까지 반복
		while (left <= end && vec[left] <= vec[pivot])
			left++;
		// 피벗보다 작은 데이터를 찾을 때까지 반복
		while (right >= start + 1 && vec[right] >= vec[pivot])
			right--;

		// left와 right가 엇갈렸다면
		if (left > right) {
			int temp = vec[right];
			vec[right] = vec[pivot];
			vec[pivot] = temp;
		}
		// 아직 left와 right가 엇갈리지 않았다면
		else {
			int temp = vec[left];
			vec[left] = vec[right];
			vec[right] = temp;
		}
	}

	// 피벗 기준 분할하였으면 각각의 분할 구간 다시 정렬(재귀 방식)
	quickSort(vec, start, right - 1);
	quickSort(vec, right + 1, end);
	
}

---

계수 정렬(Counting Sort)

시간 복잡도: O(n), 메모리: 정렬할 원소의 최소값~최대값까지의 공간이 필요

정렬할 배열에 1~k까지의 정수가 있다면, 각 숫자별로 몇 번씩 나왔는지 count하고, 이 카운팅이 입력된 별도의 배열을 바탕으로 정렬을 하는 것이다.

시간 복잡도는 원소의 갯수 n과 k의 합인 O(n+k)가 요구되지만, 그만큼 메모리를 소모해야하는 정렬 방식이다.

---

참고1, 선택/삽입/퀵 정렬은 비교 기반의 정렬 알고리즘.

메모리 소모를 감수하며 O(n) 급의 시간복잡도 정렬 방식인 '계수 정렬'(counting sort) 존재

참고2, main 함수

int main(){
    int n;
    cin >> n;

    vector<int> vec(n);
    for(int i=0; i<n; i++){
        int x;
        cin >> x;
        vec[i] = x;
    }

    vector<int> sorted = selectionSort(vec);
    vector<int> sorted2 = insertionSort(vec);

    cout << "정렬 전" << '\n';
    for(int i=0; i<n; i++){
        cout << vec[i] << ' ';
    }
    cout << '\n';

    cout << "선택 정렬 후" << '\n';
    for(int i=0; i<n; i++){
        cout << sorted[i] << ' ';
    }
    cout << '\n';

    cout << "삽입 정렬 후" << '\n';
    for(int i=0; i<n; i++){
        cout << sorted2[i] << ' ';
    }
    cout << '\n';
}