알고리즘(Algorithm)
1.자료형 범위(C/C++)/코테 시간복잡도
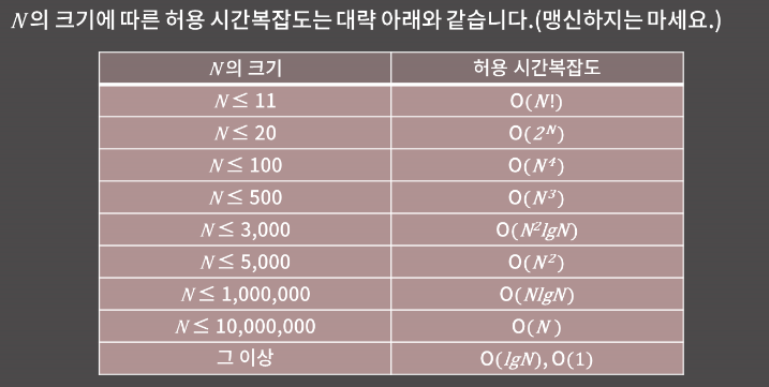
int / 4바이트 / –2,147,483,648 ~ 2,147,483,647 => 1,000,000,000까지의 수 범위를 담을 수 있음. long long / 8바이트 / –9,223,372,036,854,775,808 ~ 9,223,372,036,854,775,
2.헤더 정리

min(a, b) max(a, b)
3.[정렬] 정렬 종류와 시간 복잡도
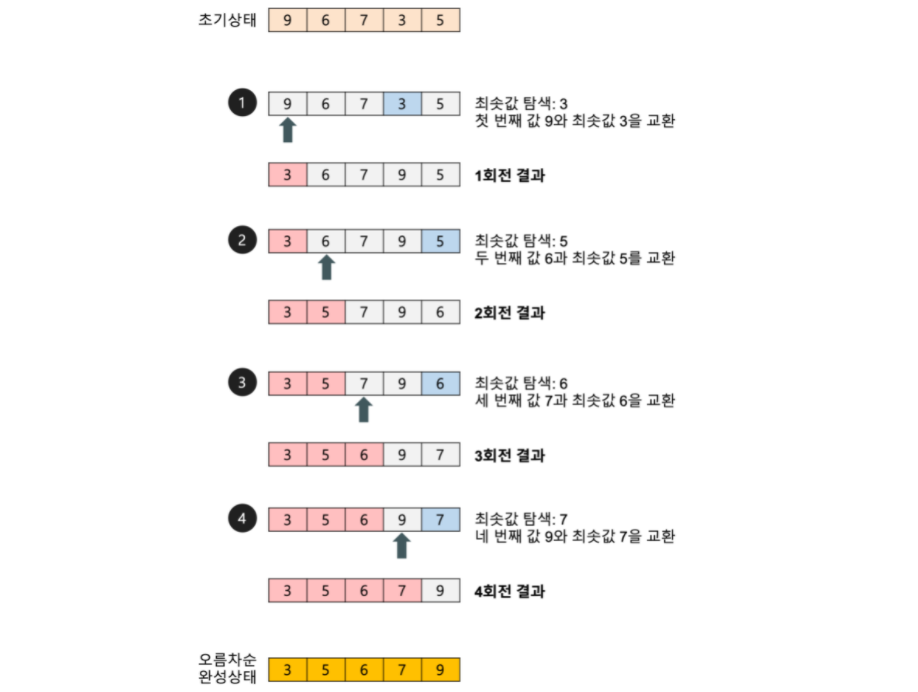
시간 복잡도: O(n^2)회전시마다 앞쪽 요소들은 정렬된 상태가 된다. 삽입 정렬 또한 시간 복잡도는 O(n^2)이다. 다만 련재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작!!최선의 경우: O(n)최악의 경우: O(n^2)보통의 경우 삽입 정렬보다
4.[map, set] map, set 정렬, 사용자 구조체 담기 / 문제 풀이: 샘플제품사진_LG swedu

map, set에 ket, value pair 또는 key를 삽입할 시 자동으로 오름차순 정렬된다. 내림차순 정렬로 바꾸고 싶다면 greator<int>를 사용한다. 여기서 int는 key의 자료형이다. set 자료구조도 value만 없을 뿐 위 방식과 동일하게
5.배열, vector 초기화

\-858993460 -858993460 -858993460\-1 -1 -1\-1 -1 -1\-1 - 1 -1\-1 -1 -1\-1 -1 -1\-1 -1 -1\-1 -1 -1\-1 -1 -1\-1 -1 -1size of vec: 3지역으로 선언되더라도 요소들이 자동 0
6.트리 / 이진트리 / 힙(완전 이진트리 기반)
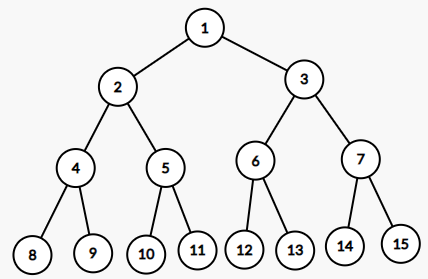
레벨 i에서의 노드의 최대 개수는 2^i개 (0 <= i)높이가 h인 이진트리가 가질 수 있는 노드의 최소 갯수는 (h+1)개 (0 <= h)높이가 h인 이진트리가 가질 수 있는 노드의 최대 갯수는 (2^(h+1)-1)개 (0 <= h)1\. 포화 이진
7.vector와 string 추가 메서드 - 짝지어 제거하기(프로그래머스)
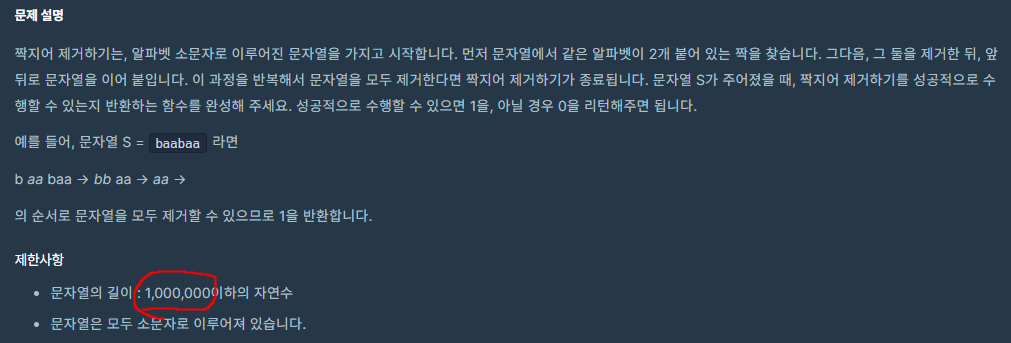
auto iter = vec.begin(); // 첫번째 원소를 가리킴auto iter = vec.end(); // 마지막 다음을 가리킴 str 문자열 중 str2 문자열이 포함되어 있다면 시작 인덱스를 반환한다.
8.[DP, 그리디] 0/1 배낭문제 vs 분할가능 배낭문제

여러 물건들의 가치(v)와 무게(w)가 주어지고, 가방의 최대 사이즈(maximum size)가 주어질 때 가치들의 합이 가장 높도록 물건을 가방에 담는 알고리즘이다. 먼저 분할가능 배낭문제는 간단한 그리디 알고리즘이다. 단위 무게당 가치 순으로 높은 것들부터 담는 욕
9.[이진 탐색(Binary search)] 템플릿 코드와 예제 문제: 기타레슨_백준, 입국심사_프로그래머스

약 10,000,000(10M)개의 원소가 존재하는 배열이나 벡터에서 특정값을 검색하는 알고리즘은 순차탐색과 같은 O(n)의 시간복잡도 알고리즘으로 해결할 수 있으나 그 이상은 O(logn)의 시간복잡도를 가진 알고리즘을 해결해야 한다. 이때 이진탐색(binary se
10.[이진 탐색(Binary search)] 예제 문제2: 두 용액_백준
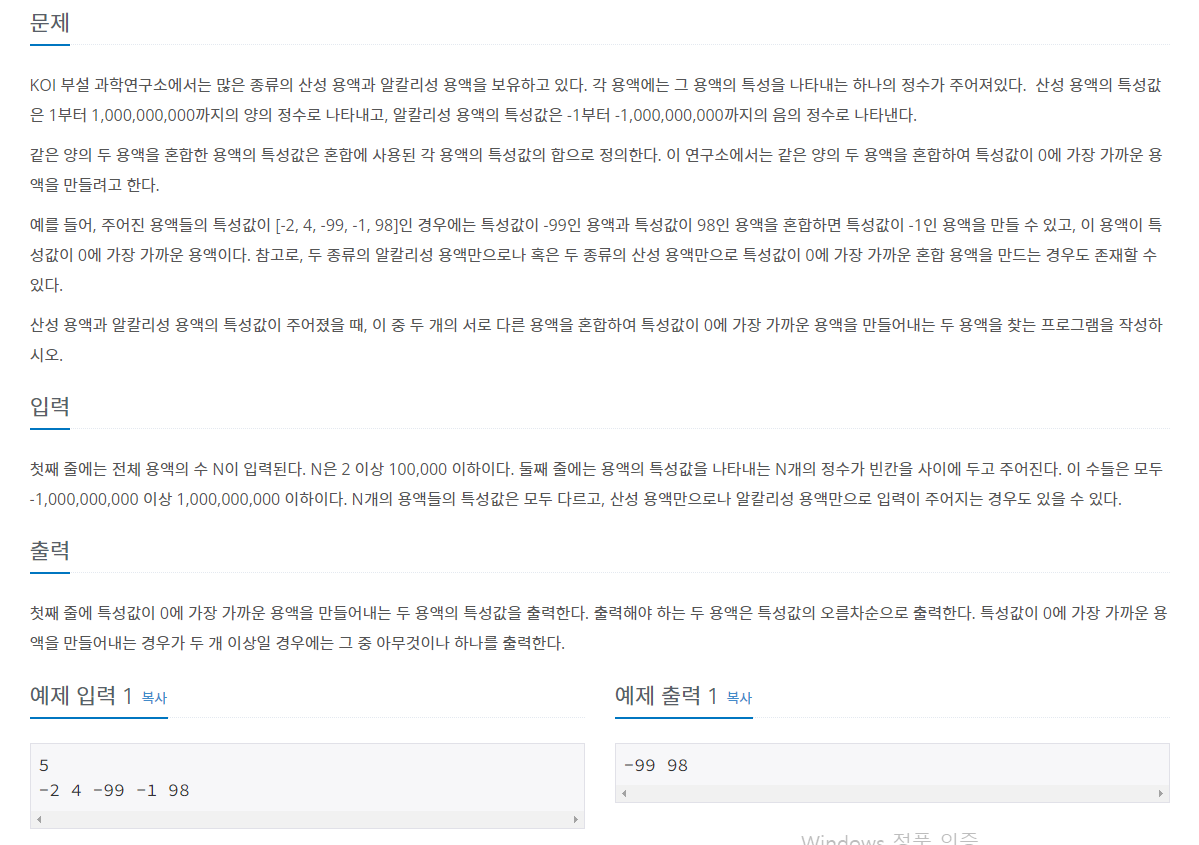
이진 탐색 문제는 탐색의 대상을 찾는 것이 중요하다. 이전 포스팅의 문제들은 이진탐색을 하는 과정에서 mid의 값이 결정될 때 마다 해당 mid를 바탕으로 요구조건을 충족하는지에 대한 판단이 있었다. 따라서 시간 복잡도가 O(logN) \* O(k)와 같았다.반면 아래
11.[Lower_bound/Upper_bound] 개념과 예제 문제: 개똥벌레_백준

https://programmers.co.kr/learn/courses/30/lessons/43238수의 범위를 보니 이진탐색임을 감지.탐색의 범위 설정 \-> 0 ~ 심사시간이 가장 긴 시간 \* (n / times.size())for(times.size()
12.[구간합] 개똥벌레_백준 구간합 풀이법

13.[DFS, DP] 재귀호출 시간복잡도 계산 & DFS+DP 풀이: (백준)2×n 타일링 2

source: https://www.youtube.com/watch?v=NyV0d5QadWM=> 시간 복잡도: O(branch^depth)ex) 재귀호출 방식의 피보나치 수열 시간복잡도=> O(2^n)source: https://www.youtube.
14.[DFS] 가지치기? 메모제이션?

DFS 풀이에서 시간을 단축시키는 방법은 크게 "가지치기"와 "메모제이션"이 있다.최소값을 구하는 경우, 중간 값이 이전에 구한 최소 값보다 크다면(좋지 않다면) 해당 경우는 가지치기할 수 있다.그러나 최대값을 구하는 경우에는 중간 값이 이전에 구한 값보다 작음을 판단
15.백트래킹 - N과 M (백준)
백트래킹 = DFS(탐색) + 조건문을 통한 가지치기 => 효율적인 탐색
16.[위상 정렬] 개념과 예제 문제: 문제집_백준
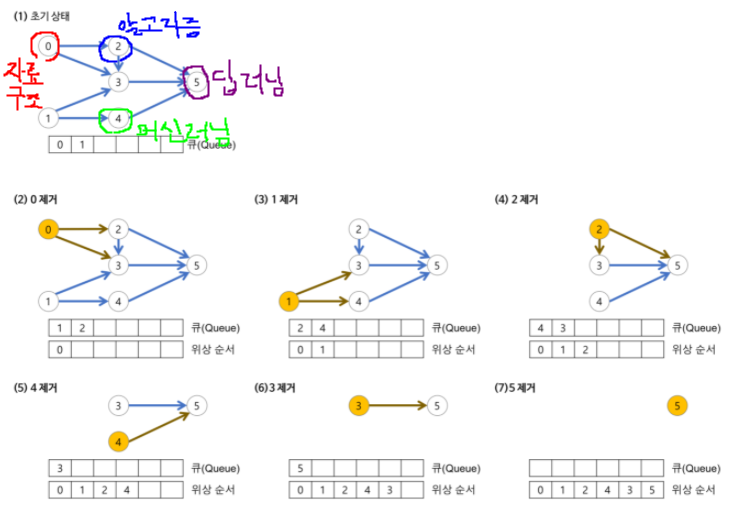
위상 정렬(topology sort)은 정렬 알고리즘의 일종.순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘.위상 정렬이란 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것전형적인 예시로는 '선수과목'을 고려
17.[위상 정렬] ACM CRAFT(백준) - DFS 시간초과=>메모제이션 추가 / + 위상정렬 풀이법
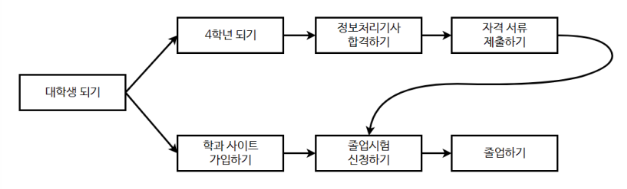
위상정렬 풀이법
18.[진법변환] 예제 문제: 진법 변환2_백준
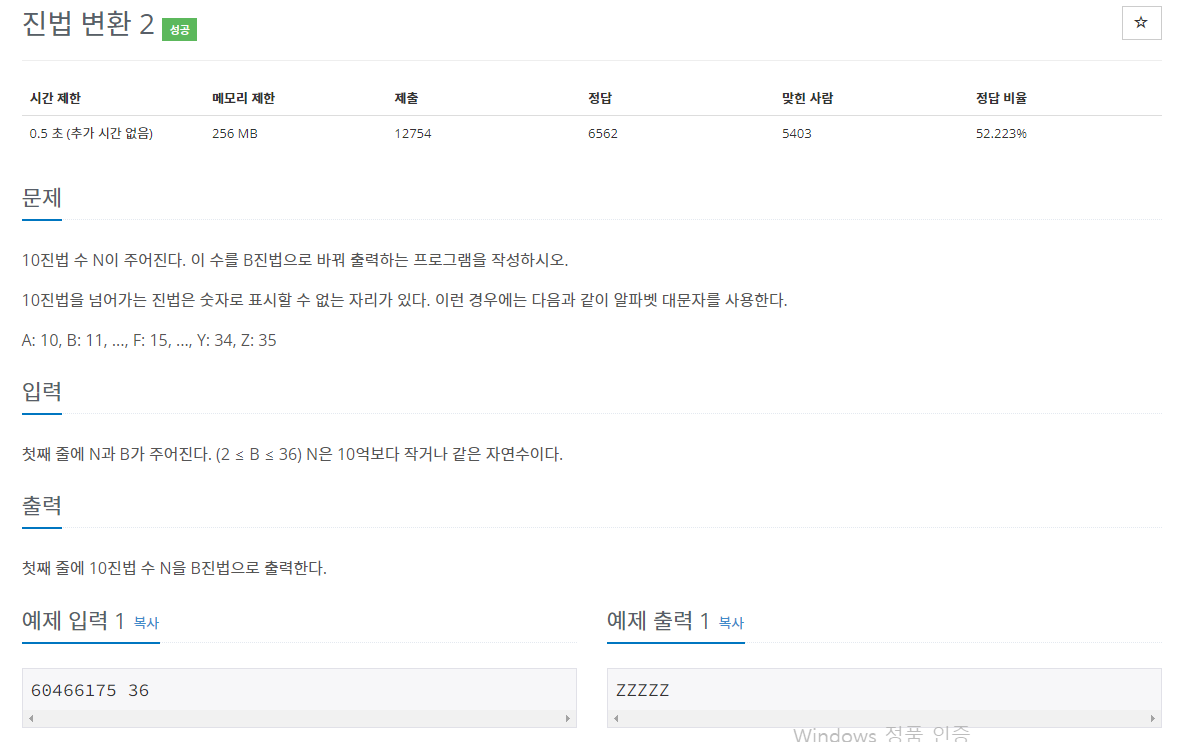
아주 복잡하게 푼 방식 => 시간초과무식한 방법인 듯..
19.[투 포인터] 예제 문제: 수들의 합 2_백준
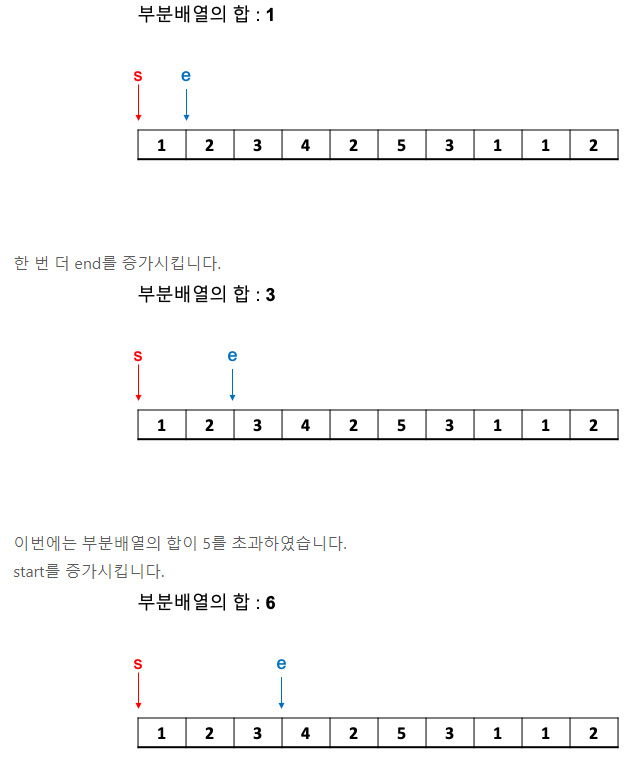
두 개의 인덱스(포인터)를 이용하긴 했지만 적절하지 않은 풀이 <= 시간 증가!why? 이걸 굳이 할 필요가 없음. source: https://ssungkang.tistory.com/entry/Algorithm-Two-Pointers-%ED%88%AC-
20.[유니온-파인드] 개념과 예제 문제
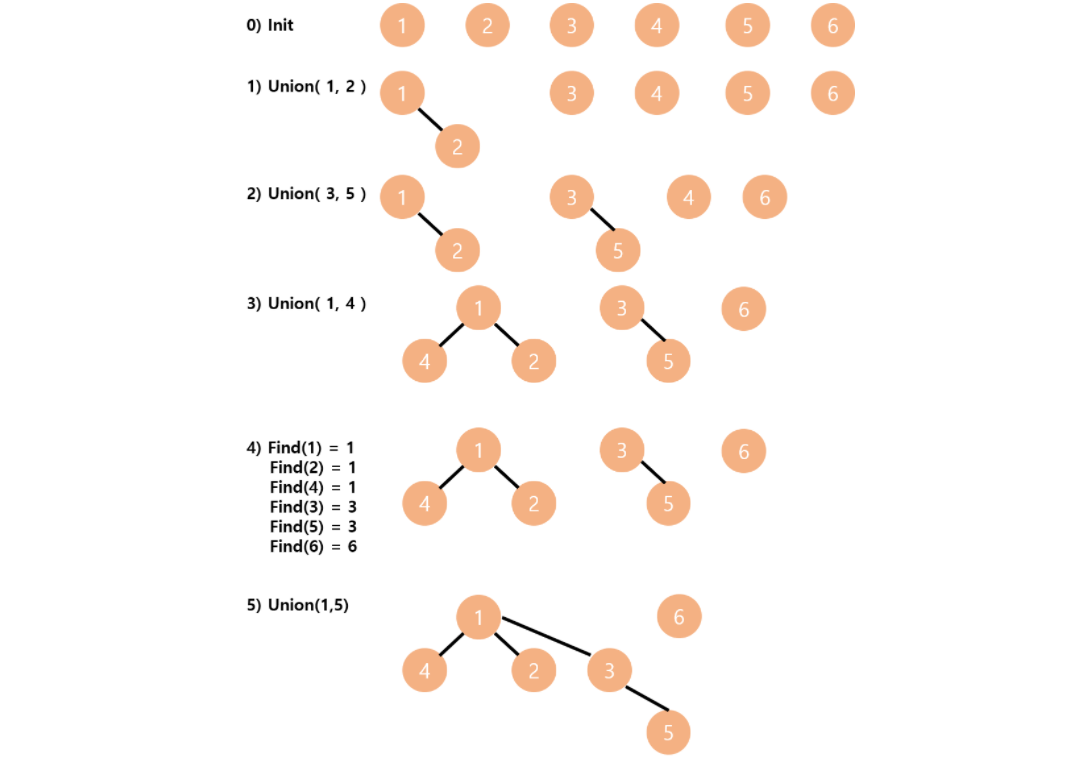
입력6 41 42 32 45 6출력1 1 1 1 5 5 <= 각 원소가 속한 집합1 1 2 1 5 5 <= 부모 테이블
21.[유니온-파인드] 예제 문제: 거짓말_백준
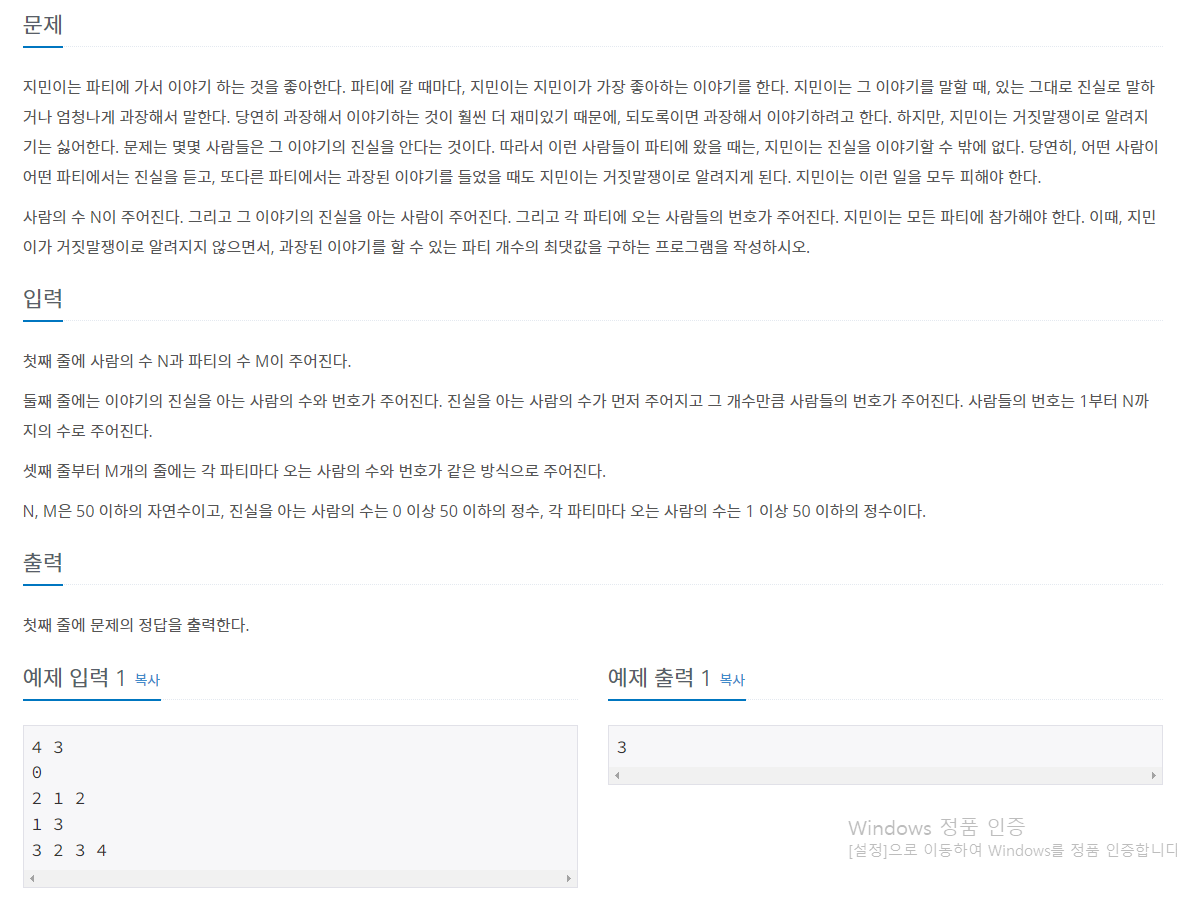
백준 거짓말: https://www.acmicpc.net/problem/1043참고)main의 vector<T> arr\[m]을 전달받는 함수=> void func(vector<T> \*arr, m)나의 풀이 => O(N^3\*LogN)참고: htt
22.[유니온-파인드] 무방향 그래프 속 사이클 찾기 / 예제 문제: 사이클 게임_백준

유니온 파인드 집합(서로소 집합)은 다양한 알고리즘에 사용될 수 있으며, 그 중 무방향 그래프 내에서 사이클을 판별할 때 사용할 수 있다. Union 연산은 그래프에서의 간선으로 표현될 수 있다. 즉 하나의 union 연산이 하나의 간선 연결과 같다. 따라서 간선을 하
23.[사이클 탐색] 무방향 그래프, 방향 그래프 안 사이클 탐지
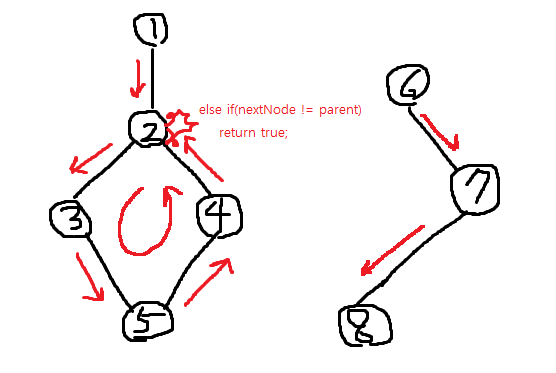
무방향 그래프 안에서의 사이클 탐색 알고리즘을 쓴다면, 즉 visited 배열을 통해 사이클 탐지를 확인하면 사이클이 아닌 것도 사이클로 식별될 수 있다. 따라서 추가적인 배열이 필요하다.
24.[사이클 탐색] 방향 그래프, DFS로 해결 / 예제 문제: 텀 프로젝트_백준
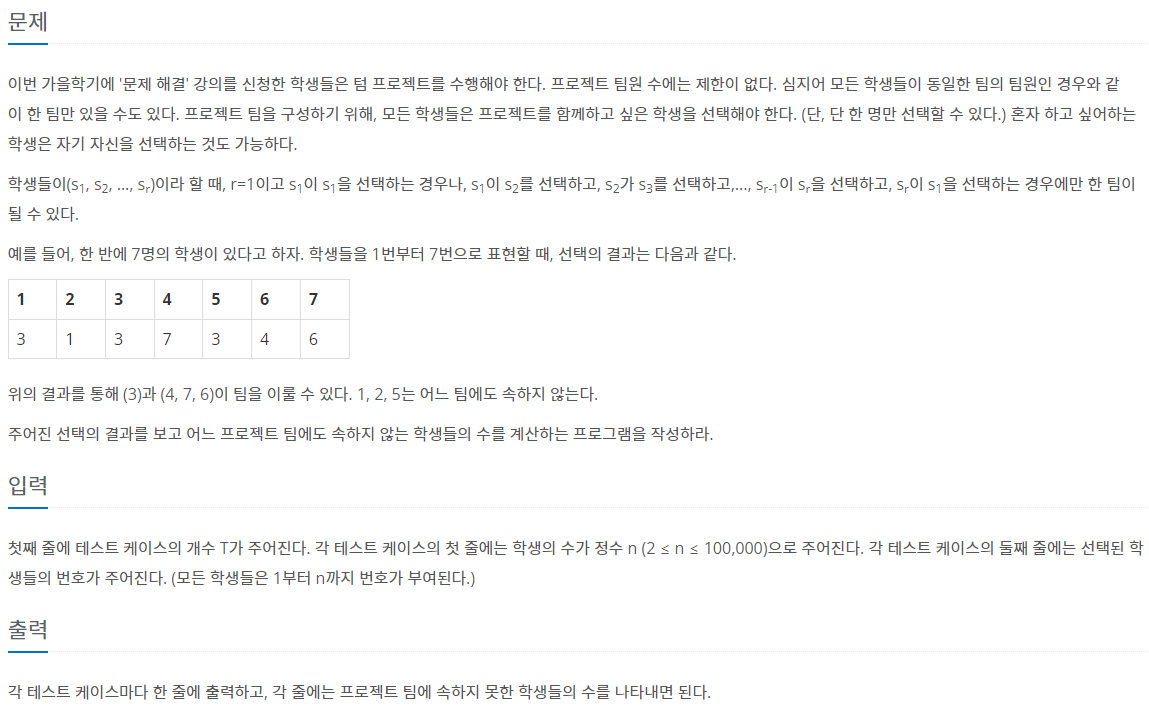
source: https://www.acmicpc.net/problem/9466
25.[MST(최소 신장트리), 그리디] 크루스칼 알고리즘과 예제 문제

신장트리는 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않은 그래프를 의미하며, 사이클이 존재하지 않는다는 조건은 곧 트리의 성립 조건이므로 이러한 그래프를 '신장트리'라고 한다. 모든 도시를 '연결'할 때, 최소한의 비용으로 연결 <= 최소
26.[MST(최소 신장트리)] 크루스칼 알고리즘과 예제 문제2: 별자리 만들기 (+ 소수점 자리 조절)
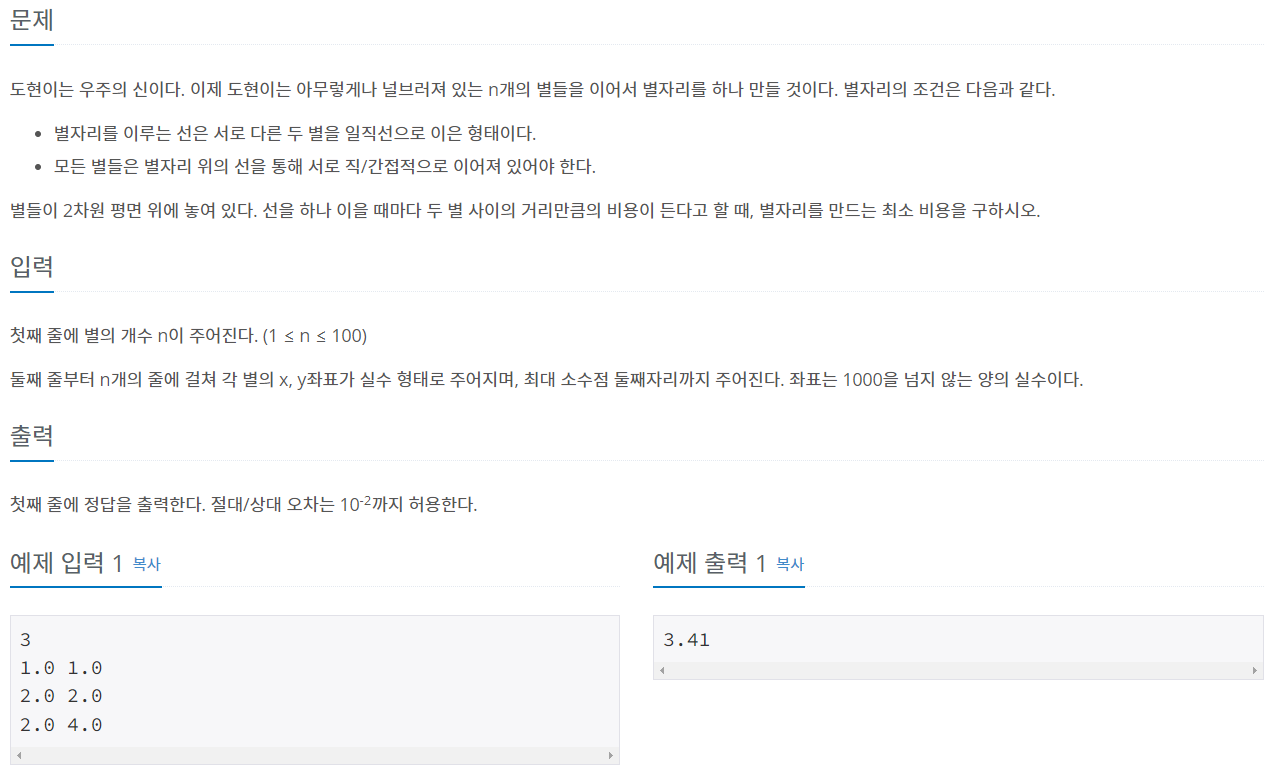
reference: https://www.acmicpc.net/problem/4386
27.[LCA (Lowest Common Ancestor) (가장 가까운 조상 찾기)] 개념과 예제 문제: LCA_백준
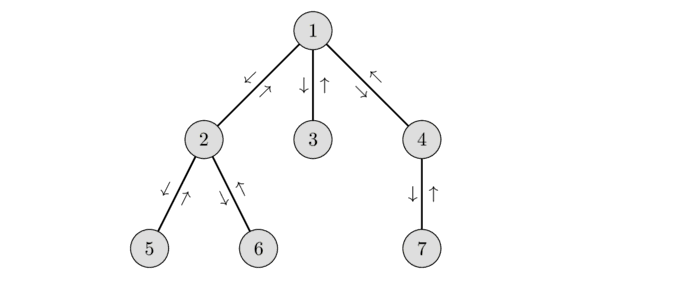
source: https://cp-algorithms.com/graph/lca.html위와 같은 그림이 있다. 그림의 트리는 전재조건이 있다.1) 자식노드의 번호는 부모노드의 번호보다 작다.2) 같은 깊이에서 왼쪽 노드의 번호가 더 작다. 이 경우 두 노드의
28.[소수] 소수 판별 알고리즘과 예제 문제: 소수 구하기_백준, 에라토스테네스의 체_백준
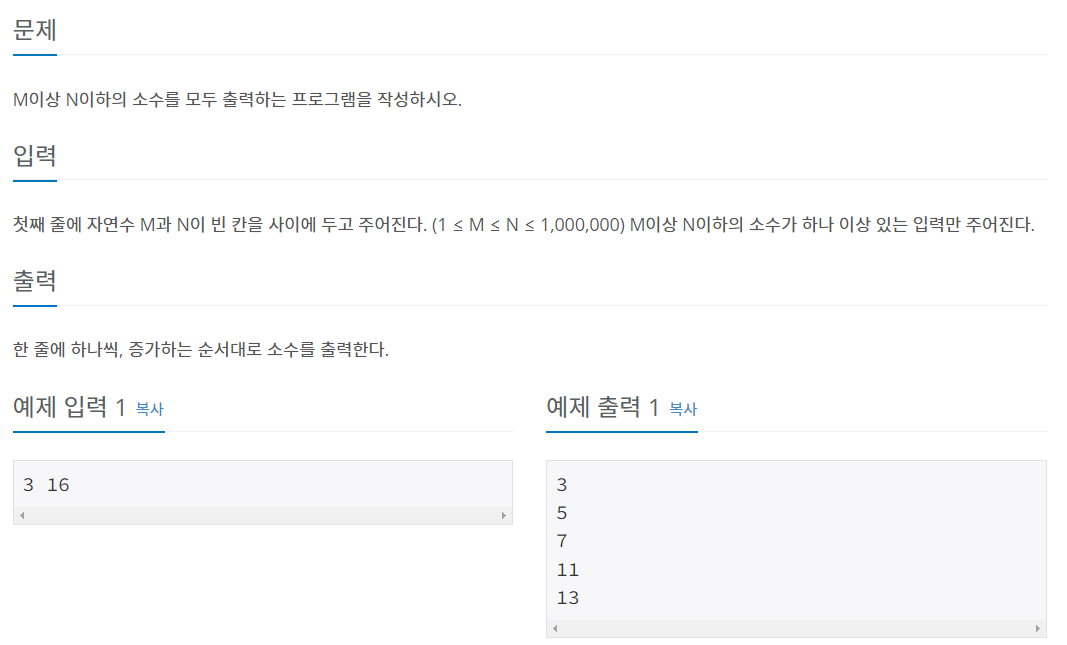
시간 복잡도 O(N)의 방법시간 복잡도 O(sqrt(N))의 방법N의 약수의 약수(?)는 무조건 sqrt(N) 범위 안에 존재한다.숫자 12를 예로 들자면,sqrt(12) = 3.xxx12의 약수는 1, 2, 3, 4, 6, 12이다.소수가 아닌 1과 12를 제외하고
29.[그래프 탐색, DFS] 이분 그래프와 예제 문제: 백준 1707번
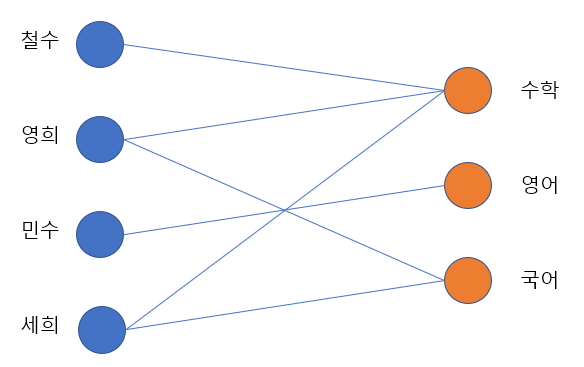
이분 그래프는 정점을 두 개의 집합으로 나눌 수 있는 그래프이며, 이때 그래프의 모든 엣지는 서로 다른 집합에 속한 정점끼리만 연결되어야 한다. 학생 목록과 수업 목록이 있을 때, 학생들이 어떤 수업을 수강하고 있는지를 이분 그래프로 표현할 수 있다.또한 넷플릭스와 같
30.[다익스트라] 다익스트라 개념

하나의 노드에서 시작에서 각 노드들의 최단거리를 구한다.다익스트라 로직의 특징은 아래와 같다.1) 먼저 방문한 노드가 가장 최단거리임은 자명하다.2) 방문한 노드에 연결되어 있는 다른 노드들을 다음 최단거리 노드의 후보로 저장할 수 있다(우선순위 큐에 저장). 하지만
31.[다익스트라] 다익스트라 응용 예제 문제: 중량제한_백준, 도로포장_백준
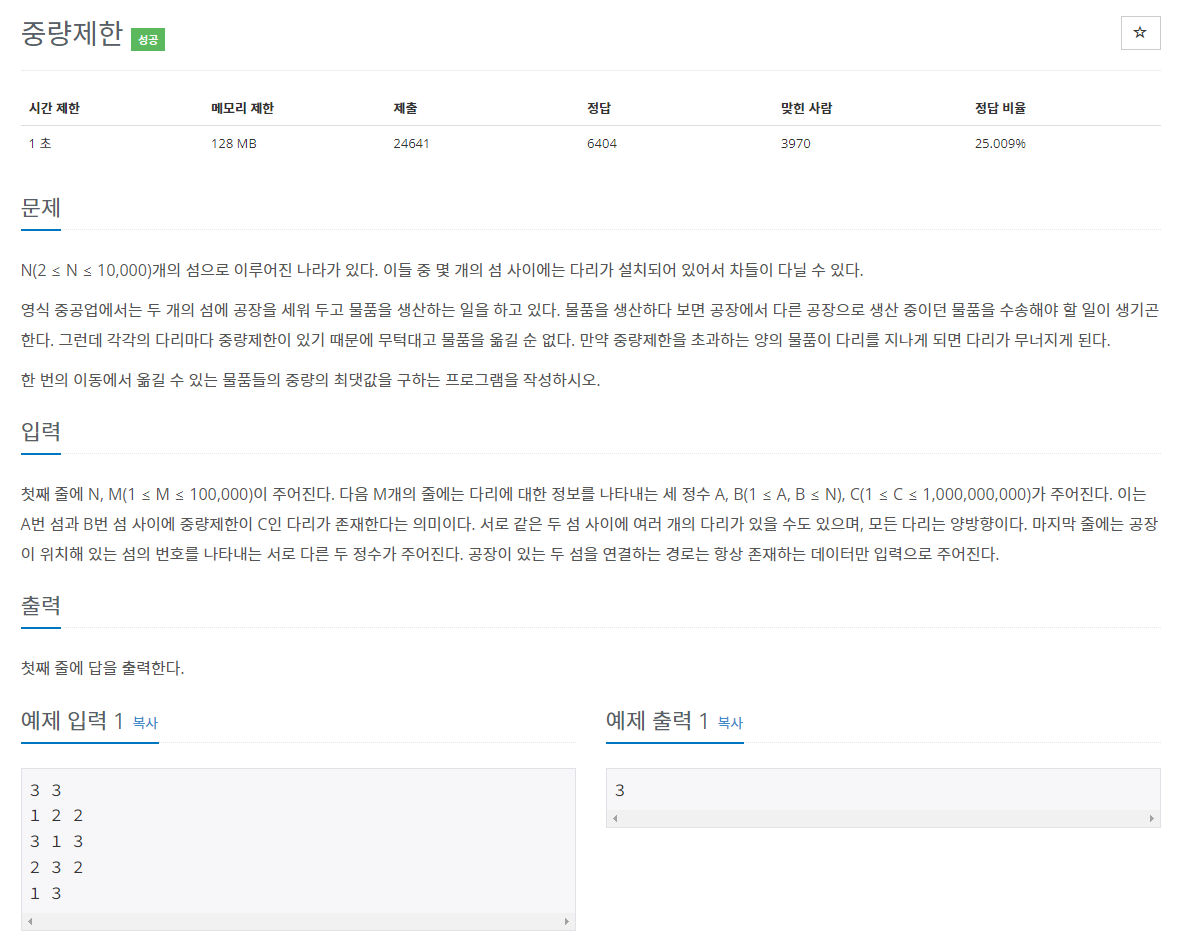
source: https://www.acmicpc.net/problem/1939source: https://www.acmicpc.net/problem/1162
32.[다익스트라] 다익스트라 응용(최적 경로 추적, 특정 간선 제외 경로) 예제 문제: 도로 검문_백준
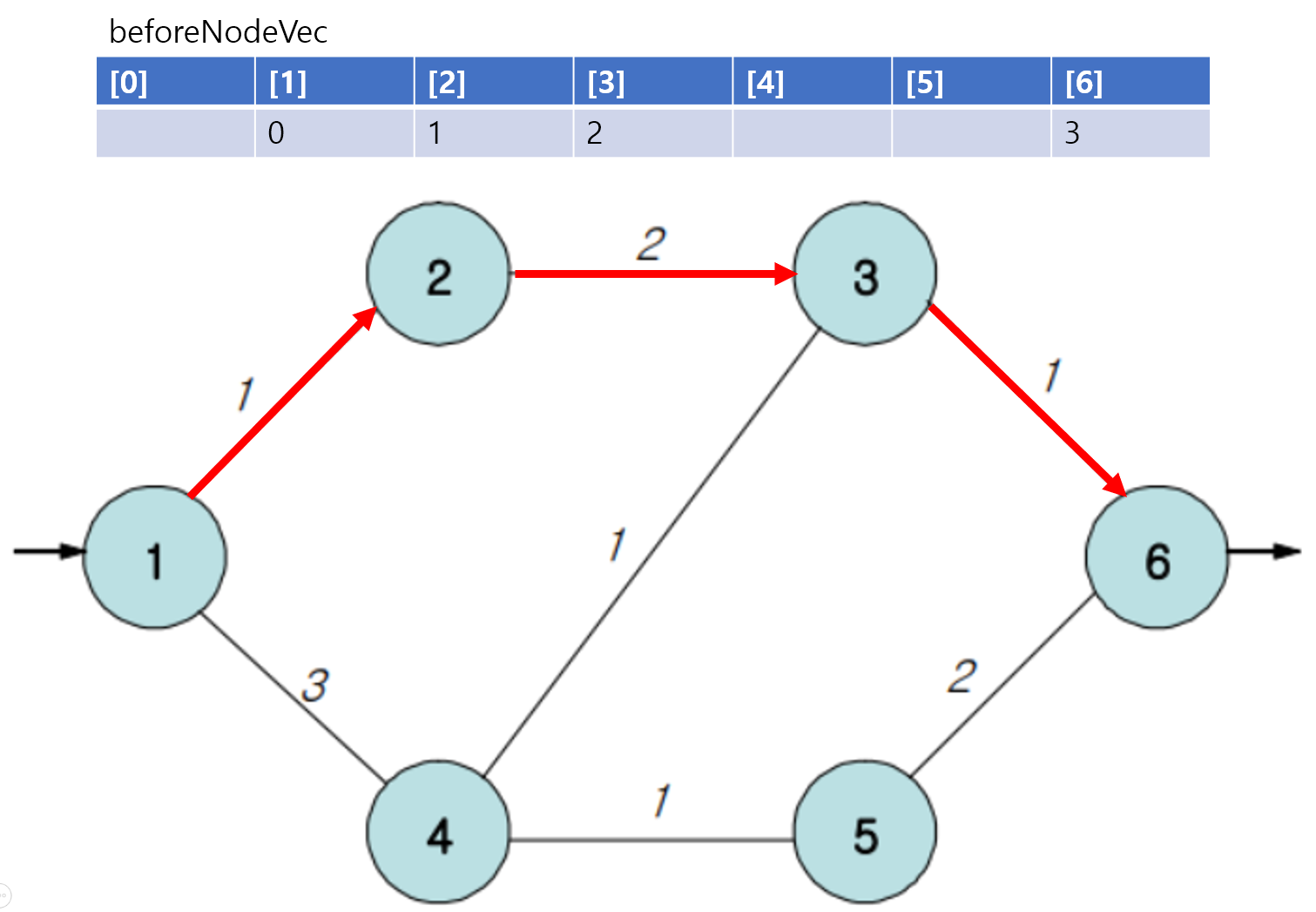
source: https://www.acmicpc.net/problem/2307(1) 경찰이 없을 때 도둑의 최적 경로 찾기(2) 도둑의 경로(도착지->출발지)를 (1) 찾은 후,해당 경로에서 하나의 간선을 빼가면서 각각 다익스트라로 최단거리 구한다. 그리고
33.[플로이드 워셜] 개념과 예제 문제
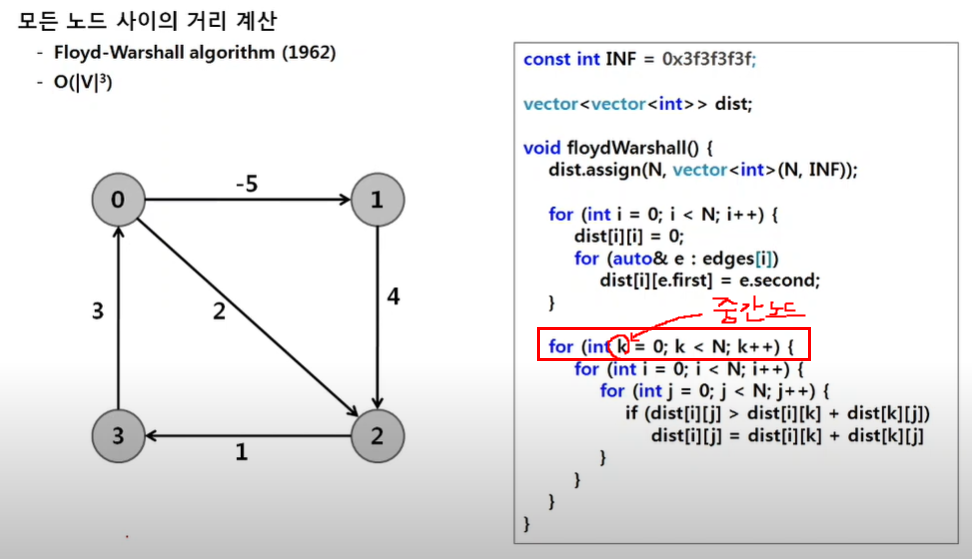
i번 노드에서 j번 노드 사이 중간 노드의 거리를 반영하여 존재하는 모든 노드를 중간 노드로 두어보며 i->j 까지의 거리를 갱신한다. 결국 i->j 간 최단 거리(최소 비용의 거리)를 찾게 된다.i와 j는 임의의 노드 번호가 될 수 있다. 결국 모든 노드 사이의 최단
34.3번의 다익스트라 (O(3*ElogV)) or 플로이드-워셜 (O(V^3)) - 특정한 최단 경로

백준 특정한 최단 경로: https://www.acmicpc.net/problem/1504(1) 다익스트라를 3번 돌린다. \- start node: 1 \- start node: mid1 \- start node: mid2(2) 경우의 수 2개
35.[구간 합(Range Sum)]
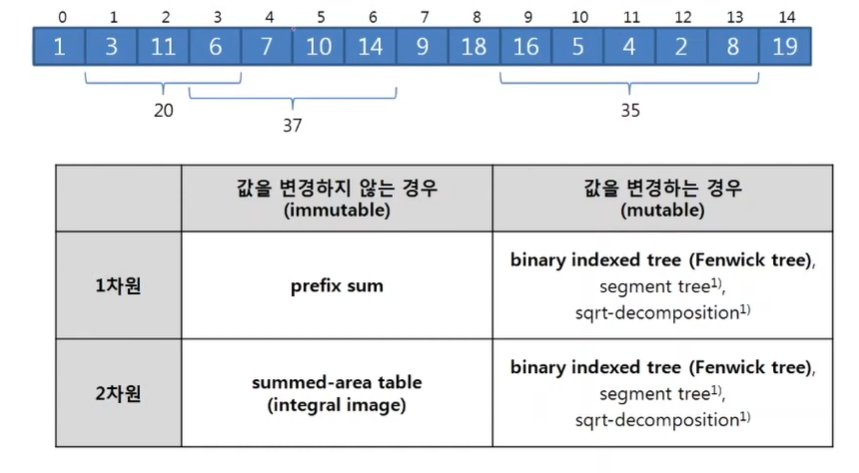
reference: https://www.youtube.com/watch?v=\_2DOKWvGets&list=PL-OC--HdIAXMXZ3IXSeLaO9Rl6qJNGc6g&index=33구간 합 문제는 '값이 변경되지 않는 경우'와 '값이 변경되는 경우'로 크
36.[LIS(Longest Increasing Subsequence)] 개념과 예제 문제: LIS 1_백준(O(n^2)), LIS 2_백준(O(nLogn))

시간 복잡도: O(N^2)로 해결 가능(탑다운) DFS + 메모제이션 방식 사용DFS 시간복잡도를 잘 계산하지 못하겠음..바텀업 방식시간복잡도: O(N^2)vec을 순차적으로 서칭.현재 idx: nowIdx , 값: nowValuedp를 채우는 조건\-> dpnowVa
37.[LIS(Longest Increasing Subsequence)] 응용 문제: 징검다리2_소프티어

source: https://softeer.ai/practice/info.do?idx=1&eid=393아래 풀이는 사실상 O(N^3)에 메모제이션 기법을 추가한 것이다. 따라서 소프티어 플랫폼에선 시간 초과가 발생하였다.앞선 포스팅의 O(NlogN)으로 LIS
38.[LCS(Longest Common Subsequence)] 개념과 예제 문제: LCS1/2_백준 (다이내믹 프로그래밍)

LCS1은 탑다운 방식 가능, 재귀의 return이 정수형이라서 가능한듯참고: https://aerocode.net/269이 페이지에서 작성자분께서 직접 LCS1 문제에 대해 탑다운 방식과 바텀업 방식의 시간을 비교해주었다.거의 두배 차이가 나네...대부분 정
39.[순열, 조합] 기본 코드 및 예제 문제: 암호 만들기, 소문난 칠공주_백준
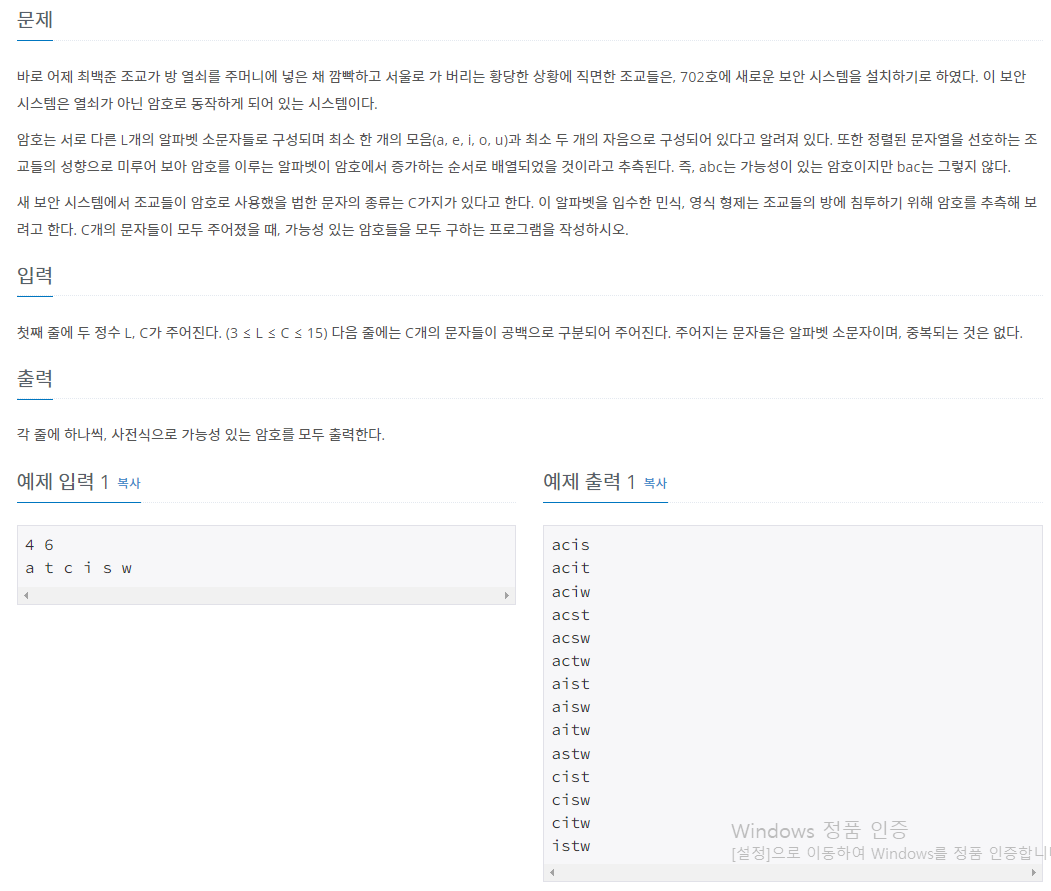
n P rn C rsource: https://www.acmicpc.net/problem/1759source: https://www.acmicpc.net/problem/1941총 25명의 학생 중에서, 7명을 뽑기, 25C7: int combinati
40.[조합] 부분수열의 합 vs 부분수열의 합2
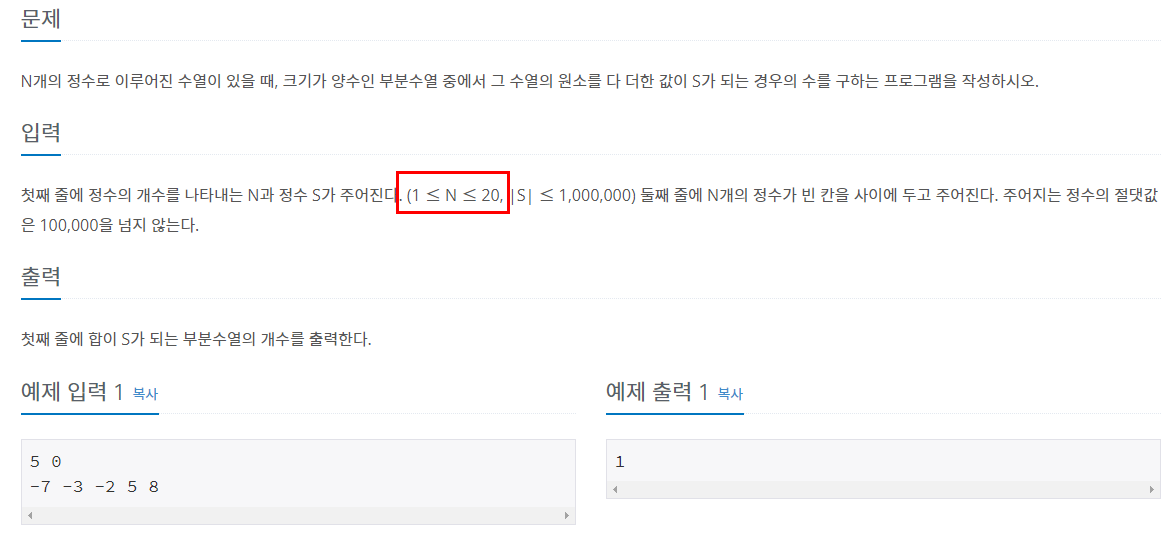
조합의 시간 복잡도에 대한 고찰을 하게된 문제이다. 이 문제는 위 코드로는 시간초과가 뜬다.왜 그럴까? nCr 의 시간복잡도: n! / (n-r)!\*r!모든 조합의 시간복잡도: nC1 + nC2 + ... + nCn = 2^n모든 조합의 시간복잡도는 2^n, 지수적
41.[조합+이진탐색] 냅색문제_백준
source: https://www.acmicpc.net/problem/1450전체 조합의 케이스를 줄이는 방식이 '부분 수열2\_백준' 문제와 유사하다.reference: https://velog.io/@jinh2352/%EC%A1%B0%ED%95%
42.힙(Heap), 우선순위 큐(priority_queue) - 더 맵게(프로그래머스)
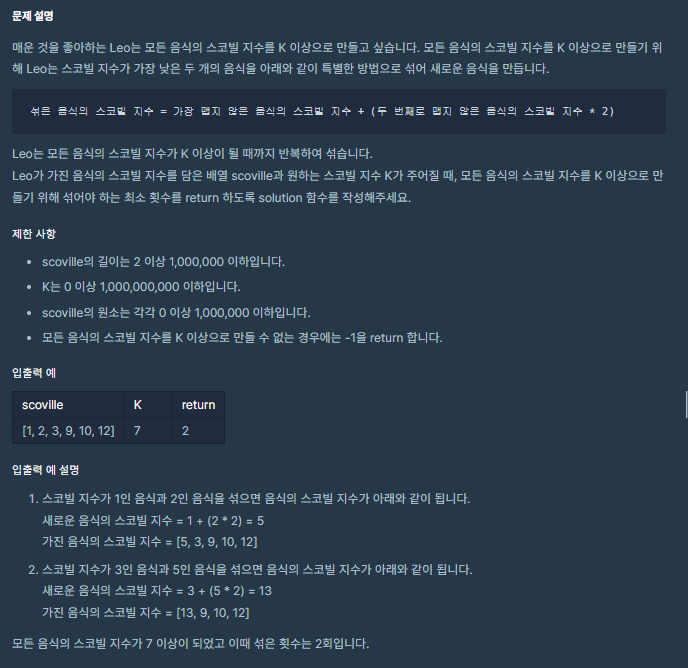
https://programmers.co.kr/learn/courses/30/lessons/42626이 문제는 힙으로 풀었어야 했다. 첫 시도는 힙으로 풀지 않아 효율성에선 통과하지 못하였다.priority_queue 이용
43.[최대공약수와 최소공배수(with 유클리드)] 템플릿 코드와 예제 문제: 멀쩡한 사각형_프로그래머스
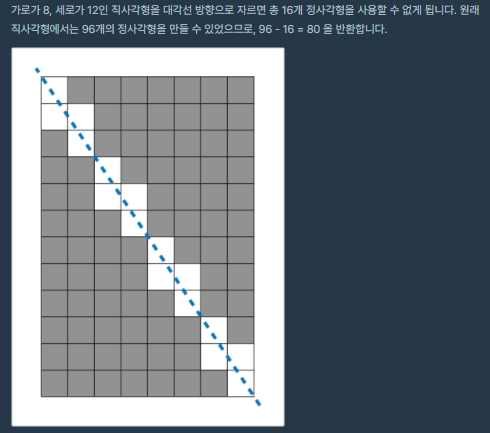
https://programmers.co.kr/learn/courses/30/lessons/62048?language=cpp이 문제는 최대공약수를 적절히 이용했어야 했다. 최대공약수를 사용하지 않아도 풀리긴 하였지만 소수 오차에 의해 단 한개의 테케가 계속 틀
44.[우선순위큐 응용] 예제 문제: 싸지방에 간 준하_백준, 철로_백준
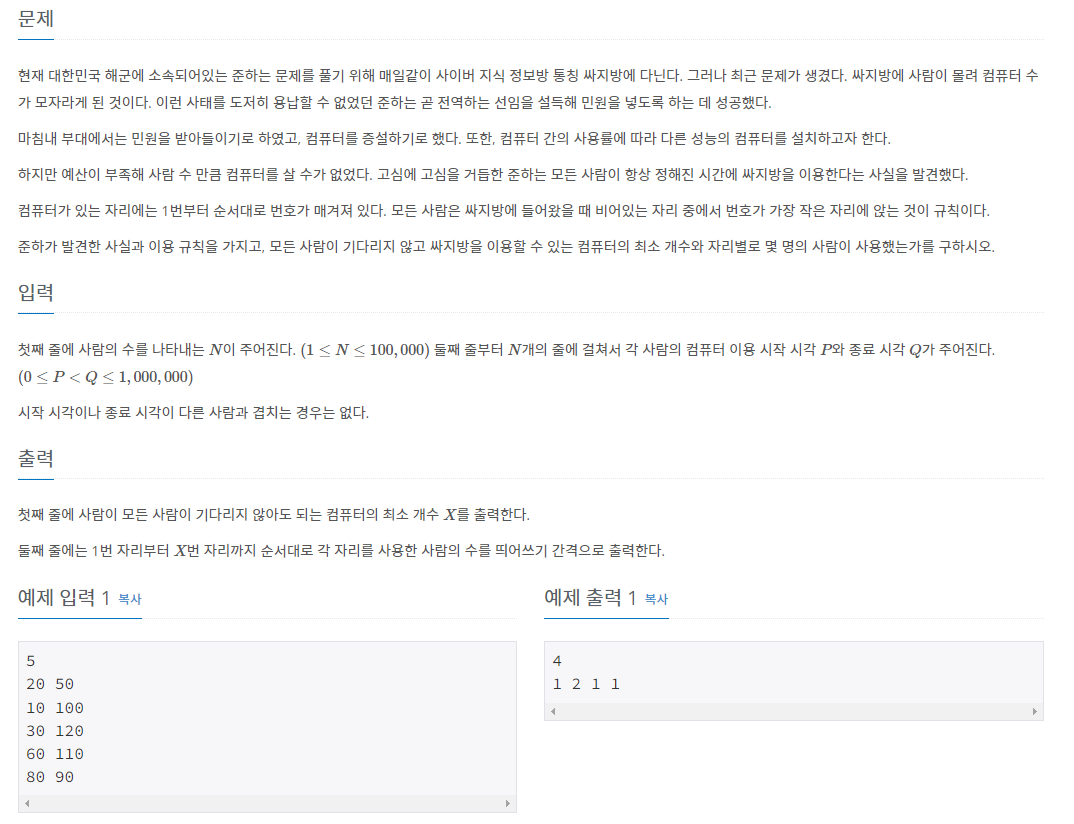
source: https://www.acmicpc.net/problem/12764, https://www.acmicpc.net/problem/13334아래 두 우선순위 큐 응용 문제의 공통점으로는 모든 인덱스를 선형으로 탐색해야 하는 오버헤드를 우선순
45.최대상금.cpp

46.팰린드롬 시리즈
시간복잡도: O(N/2)차례대로 앞부분 문자와 뒷 부분 문자를 비교한다. 입력 주의!cin을 쓰다가 scanf()나 getline() 함수를 사용하려면 사용전 cin 버퍼를 비워주자. 개행문자를 뱉어내야 한다.
47.[수학: 선분 교차] 선분 교차(ccw 활용) + 유니온-파인드: 예제 문제: 선분 그룹_백준

예제 문제: 선분 그룹_백준
48.[분할 정복] 수퍼바이러스_소프티어

source: https://softeer.ai/practice/info.do?idx=1&eid=391처음 바이러스가 K라면,1초 후: K x P x ... x P = K x P^102초 후: (K x P^10) x P x .. x P = K x P^20..N
49.[강의실 배정] 강의실 배정 문제1. 최대한 많은 수의 강의 선택

강의실 배정 문제의 유형은 크게 2가지이다. (1) 최대한 많은 수의 강의를 배정하는 것.(2) 최대한 강의실을 효율적으로 사용하는 것. => 최대한 많은 시간동안 강의가 진행되도록 하는 것.이 문제는 (1) 타입의 강의실 배정 문제이다.이 문제의 풀이는 다음과 같다.