[DP, 그리디] 0/1 배낭문제 vs 분할가능 배낭문제

Jin Hur·2021년 11월 7일

알고리즘(Algorithm)

목록 보기

8/49

공통 요구사항

여러 물건들의 가치(v)와 무게(w)가 주어지고, 가방의 최대 사이즈(maximum size)가 주어질 때 가치들의 합이 가장 높도록 물건을 가방에 담는 알고리즘이다.

분할가능 배낭문제 <- 그리디 알고리즘

먼저 분할가능 배낭문제는 간단한 그리디 알고리즘이다.
단위 무게당 가치 순으로 높은 것들부터 담는 욕심쟁이 기법을 쓰면 된다.

예를 들어,

source: https://starrykss.tistory.com/1512

위 표와 같이 7개의 물건들이 주어졌다고 가정해보자. "가격/무게"를 통해 무게 대비 가격이 높은 순으로 정렬하면,
O1 > O5 > O6 > O2 > O3 > O7 > O4 순으로 정렬할 수 있다.(내림차순)

1) O1 선택 -> 가치 합: 10, 남은 무게: 7
2) O5 선택 -> 가치 합: 22, 남은 무게: 5
3) O6 선택 -> 가치 합: 33, 남은 무게: 2
4) O2 선택 -> 가치 합: 40, 남은 무게: 0

주의할 점은 만약 마지막 물건 선택 시 해당 물건 하나를 온전히 담지 못할 수 있다. 이 때 이 물건을 잘라서 넣을 수 있다는 것이 분할가능 배낭 문제와 0/1 배낭문제의 가장 큰 차이점이다.
분할가능 배낭문제에선 (마지막 물건의)단위 무게당 가치 x 남은 무게로 가치가 높도록 물건들을 꽉꽉 담을 수 있다. 따라서 그리디가 적용 가능하다.
반면, 0/1 배낭문제는 그러하지 못하다(아래 설명에 반례 존재)

// 단위무게당 가치로 정렬하는것은 그리디 방식을 적용할 수 있는 분할 가능 배낭 문제가 가능하다.
float solution1(int n, int k, vector<pair<int, int>> input){
	
    // 단위 무게당 가치를 포함하는 자료구조 생성
    	// <단위 무게당 가치, <무게, 가치>>
    vector<pair<float, pair<int, int>>> vec; 
    for(int i=0; i<n; i++){
        int w, v;
        w = input[i].first;		// 무게
        v = input[i].second;    	// 가치

        // 단위당 가치
        float perValue = v/(float)w;

        vec.push_back({perValue, {w, v}});
    }
	
    // 단위 무게당 가치로 정렬    
    sort(vec.begin(), vec.end(), compare);

    int totalWeigh = 0;
    float totalValue = 0;

    for(int i=0; i<n; i++){
        pair<float, pair<int, int>> nowP = vec[i];
        int nowWeight = nowP.second.first;
        int nowValue = nowP.second.second;

        int resWeight = k - totalWeigh;
        totalWeigh += nowWeight;
        if(totalWeigh > k){
            // 이 if문에 걸리는 것은 마지막으로 뽑을 수 있는 물건이라는 뜻이다.
            totalValue += vec[i].first * resWeight;
            break;
        }

        totalValue += nowValue;
    }

    return totalValue;
}

0/1 배낭문제 <- 다이내믹 프로그래밍

앞서 설명하였든 0/1 배낭문제는 그 물건을 포함하거나 안하거나 둘 중 하나의 선택만을 하여야 한다.
예를 들어 다음과 같은 상황에 있다.

source: https://www.acmicpc.net/problem/12865

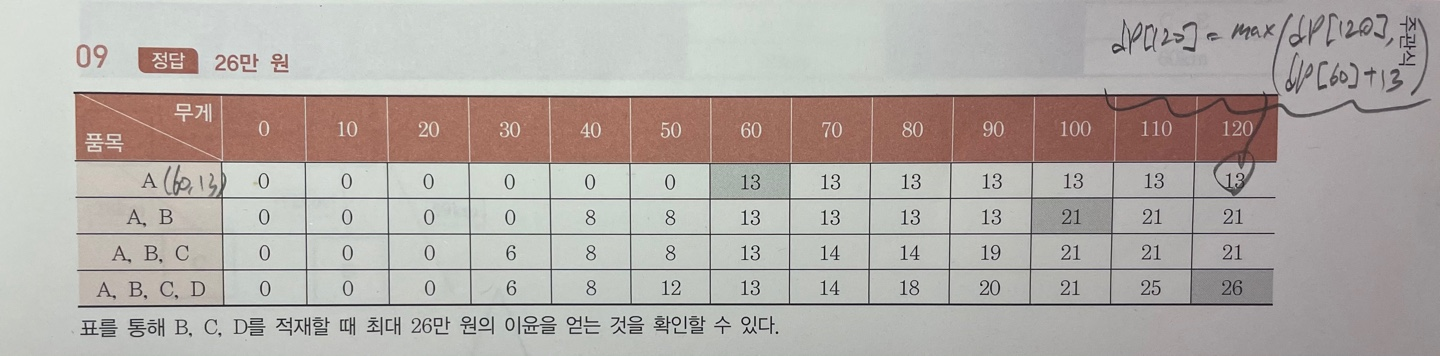
물건의 종류는 4개이고, 가방의 최대 사이즈는 7이다.
물건 1) w: 6, v: 13
물건 2) w: 4, v: 8
물건 3) w: 3, v: 6
물건 4) w: 5, v: 12

만약 분할가능 배낭문제였다면, 물건 4를 1개 선택하고, 물건 1의 1/3개를 선택하면 최대가 된다.
하지만 0/1 배낭문제는 그렇게 해서는 안된다. 0/1 배낭 문제를 단순히 무게 당 가치가 높은 것 부터 선택하면 어떻게 될까? 물건 4만을 뽑을 수 밖에 없으므로 가치합은 12가 될 것이다. 하지만 답은 물건 2와 3을 뽑은 14가 정답이다.

다이내믹 프로그래밍 해결법

탑다운: DFS + 메모제이션

DP를 통해 풀 수 있는 문제이다. 먼저 탑다운 방식이다. 그냥 DFS(조합을 위한)로는 시간초과가 뜬다. 따라서 DFS + 메모제이션을 활용한다. DP테이블은 DP[idx(특정 물건을 가리킴)][현재까지 가치합]이다.

// => 0/1 배낭문제는 다이내믹 프로그래밍

int dfs(int n, int k, vector<pair<int, int>> &vec, int idx, int weight){
    // idx번째 물건 체크 
    // 가치 합이 weight인 경우 메모한 것이 존재하는가? 
    if(dp[idx][weight] != 0)
        return dp[idx][weight];
        
    // 종료 조건
    if(weight == k)
        return 0;
    if(idx == vec.size())
        return 0;

    // 탐색
    int maxValue = 0;

    for(int i=idx; i < n; i++){
        int nowWeight = vec[i].first;
        int nowValue = vec[i].second;
        
        // 백트레킹 추가(탐색을 줄인다.)
        if(weight + nowWeight > k)
            continue;

        maxValue = max(maxValue, nowValue + dfs(n, k, vec, i+1, weight+nowWeight));
    }

    dp[idx][weight] = maxValue;
    return maxValue;    

}

int solution2(int n, int k, vector<pair<int, int>> &input){
    int answer = 0;

    answer = dfs(n, k, input, 0, 0);
    return answer;
}

바텀업

// (3) 바텀업 방식
int solution3(int n, int k, vector<pair<int, int>> &input){
    // DP 테이블 이용
    vector<int> dpTable(k+1, 0);    // 무게별로 메모하는 dp
    int answer = 0;
    
    for(int i=0; i<n; i++){                 // O(n)
        int nowWeight = input[i].first;
        int nowValue = input[i].second;
        
        // 뒤에서부터 탐색!
        for(int j=k-nowWeight; j>=0; j--){            // => O(n) * O(k)   // n <= 100, k <= 100,000
            int w = nowWeight + j;
            //if(w > k)
            //    continue;
            dpTable[w] = max(dpTable[w], dpTable[j] + nowValue);

            answer = max(answer, dpTable[w]);
        }
    }

    return answer;
}

Jin Hur