신장트리(spanning tree)
신장트리는 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않은 그래프를 의미하며, 사이클이 존재하지 않는다는 조건은 곧 트리의 성립 조건이므로 이러한 그래프를 '신장트리'라고 한다.
사이클 발생 여부를 판단하기 위해서 유니온-파인드(Union-Find) 자료구조를 활용한다.
reference: https://velog.io/@jinh2352/%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9C-%EA%B8%B0%EC%B4%88-%EC%9D%B4%EC%BD%94%ED%85%8C
크루스칼 알고리즘
모든 도시를 '연결'할 때, 최소한의 비용으로 연결 <= 최소 신장트리 생성
신장트리 중에서 최소의 비용으로 만들 수 있는 신장트리를 찾는 알고리즘을 '최소 신장트리(MST)' 알고리즘이라 하며, 대표적인 MST 알고리즘 중 하나가 바로 '크루스칼 알고리즘'이다.
- 간선 데이터를 비용(cost)에 따라 오름차순으로 정렬
- 간선을 하나씩 확인.
cf) 참고로 최종적으로 신장트리에 포함되는 간선의 갯수는 노드의 갯수 - 1이다.
WHILE(연결된 간선 수가 N-1개가 되었거나, 더이상 탐색할 간선이 없을 떄까지)
IF 두 노드의 부모가 같다면 (findParent 함수 이용)
사이클이 생성된 것 => 해당 간선 제외
ELSE
UNION 연산 => 간선 추가매 반복마다 최소 엣지 가중치를 선택하기에 그리디 방식이라 할 수 있다.
구현
입력
7 9 (노드의 수, 간선의 수)
1 2 29 (노드a, 노드b, cost)
1 5 75
2 3 35
2 6 34
3 4 7
4 6 23
4 7 13
5 6 53
6 7 25
출력
159
#include <bits/stdc++.h>
using namespace std;
// 간선의 cost 기준으로 정렬할 때 필요한 compare 함수
bool compare(pair<pair<int, int>, int> a, pair<pair<int, int>, int> b) {
return a.second < b.second;
}
// 특정 노드의 부모 탐색
int findParent(vector<int> &parentTable, int node) {
if (parentTable[node] == node)
return node;
return parentTable[node] = findParent(parentTable, parentTable[node]);
}
int solution(vector<pair<pair<int, int>, int>> &graph, int n) {
int cnt = 0;
int totalCost = 0;
// 신장트리는 사이클이 없는 그래프, 사이클 발생 여부를 판단하기 위해 유니온-파인드 자료구조 활용
// 유니온-파인드 자료구조를 활용하기 위해 parent table 생성
// parent table
vector<int> parentTable(n + 1);
for (int i = 1; i <= n; i++) {
parentTable[i] = i;
}
// 가중치 기준 오름차순 정렬
sort(graph.begin(), graph.end(), compare);
// graph를 순회하며 find, union 반복
for (int i = 0; i < graph.size(); i++) {
// 종료 조건
// 신장트리의 간선 수 = 노드 수 - 1
if (cnt == n - 1)
break;
int a = graph[i].first.first;
int b = graph[i].first.second;
int a_parent = findParent(parentTable, a);
int b_parent = findParent(parentTable, b);
// 만약 부모가 같다면 => 사이클 형성 => 무시
if (a_parent == b_parent)
continue;
// 다르다면 => 유니온 & 해당 간선 포함
else {
// 유니온(UNION)
if (a_parent < b_parent)
parentTable[b_parent] = a_parent;
else
parentTable[a_parent] = b_parent;
// 간선 포함
totalCost += graph[i].second;
cnt++;
}
}
if (cnt == n - 1)
return totalCost;
else
return -1;
}
int main() {
int n, e; // n: 노드의 수, e: 간선의 수
cin >> n >> e;
vector<pair<pair<int, int>, int>> graph;
for (int i = 0; i < e; i++) {
int a, b, cost;
cin >> a >> b >> cost;
graph.push_back({ {a, b}, cost });
}
int result = solution(graph, n);
cout << result << '\n';
}예제 문제: 도시 분할 계획

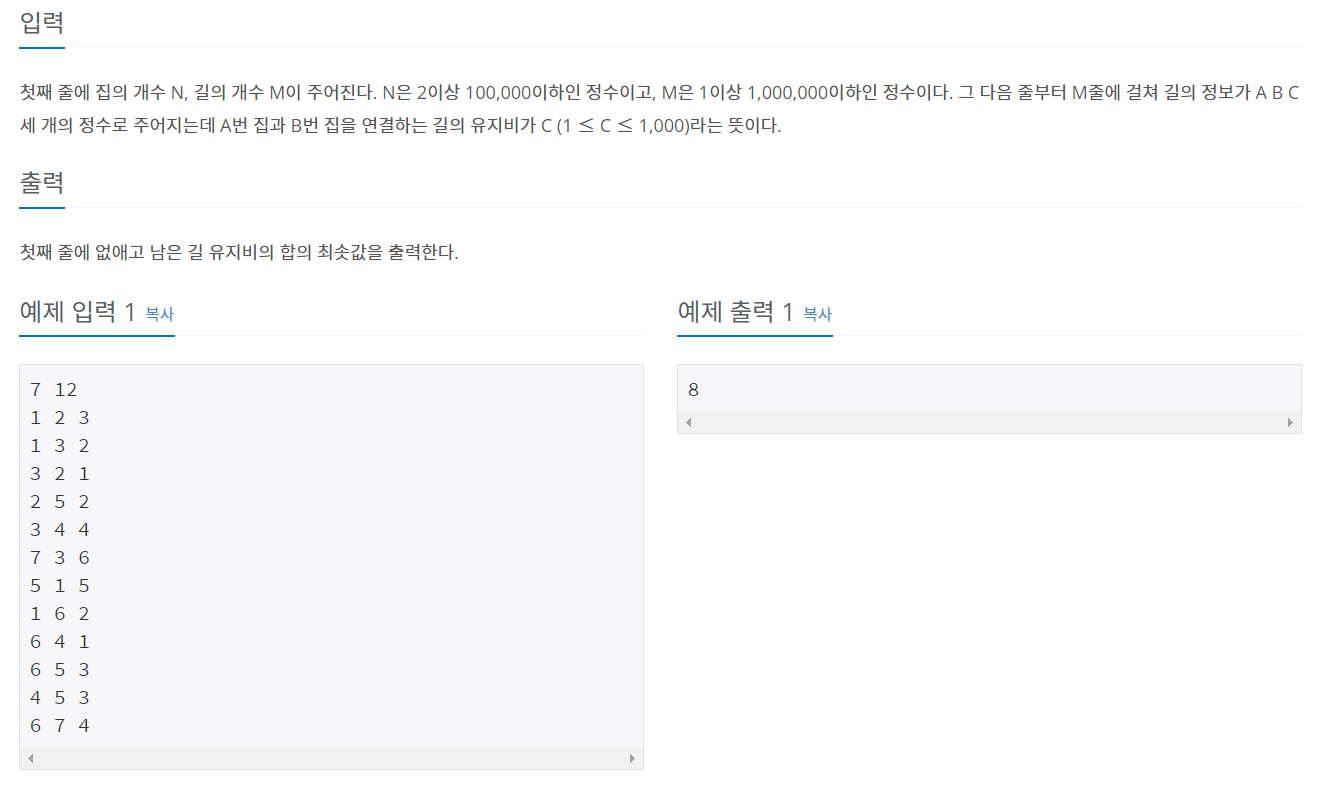
풀이
(1) 마을 안에서 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 없앨 수 있다. 그러면서 길의 유지비를 최소로 만든다.
=> 최소 신장트리 생성
예를 들어 아래 그림과 같은 길을 갖는 마을이 있다 하자
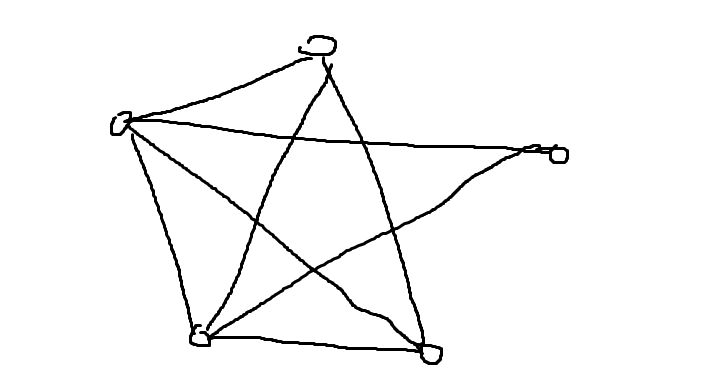
경로들의 합이 최소가 되면서, 모든 노드들을 잇도록 다음과 같이 최소 신장트리를 만들 수 있다.
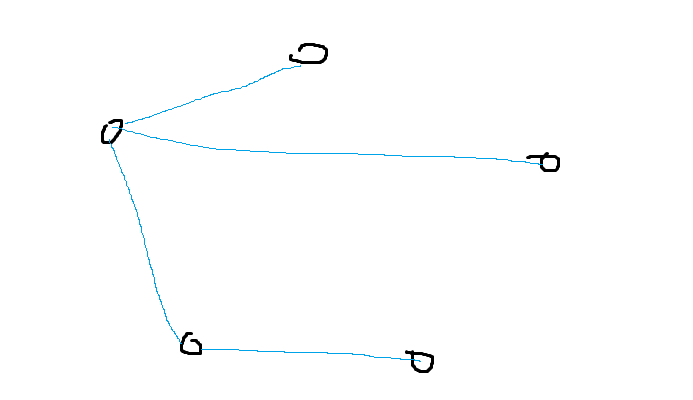
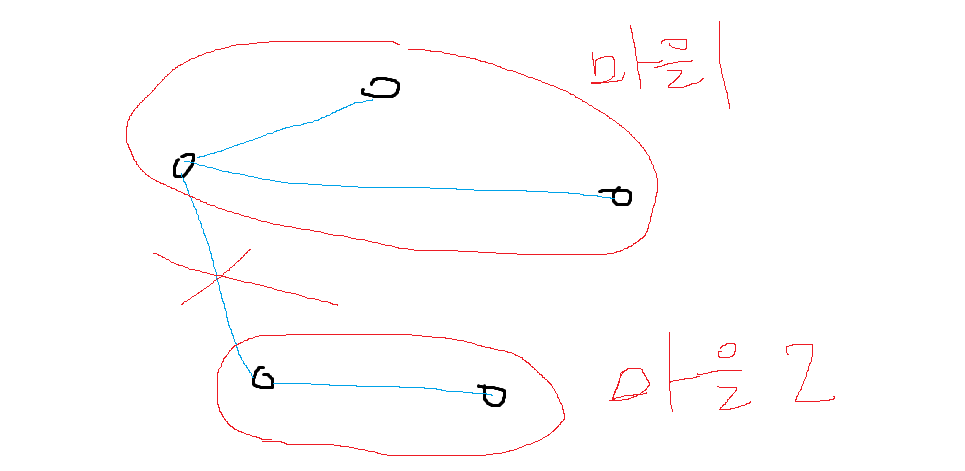
(2) 마을을 두 개로 분리한다. 분리된 마을에는 집이 하나 이상 있어야 한다.
=> 최소 신장트리에서 길 비용이 가장 큰 것을 삭제한다.
=> 최소 신장트리 생성 완성 조건을 (엣지 갯수 == 노드 갯수 - 1)이 아닌 (엣지 갯수 == 노드 갯수 - 2)로 두면 자연스럽게 가장 비용이 높은 간선(신장트리에 포함될)을 제외하게 된다.
마을의 최소 집의 갯수가 하나이니 어떤 길이든 삭제해도 된다.
소스 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M;
vector<vector<int>> loadInfo(1000000);
vector<int> parentTable(100000 + 1);
bool compare(const vector<int>& a, const vector<int>& b) {
return a[2] < b[2];
}
int Find(int node) {
if (parentTable[node] == node)
return node;
return parentTable[node] = Find(parentTable[node]);
}
void Union(int nodeA, int nodeB) {
int parentA = Find(nodeA);
int parentB = Find(nodeB);
if (parentA < parentB)
parentTable[parentB] = parentA;
else
parentTable[parentA] = parentB;
}
bool checkSameParent(int nodeA, int nodeB) {
if (Find(nodeA) == Find(nodeB))
return true;
else
return false;
}
// 제외되는 간선 번호
long long solution() {
// parentTable 초기화
for (int i = 1; i <= N; i++) {
parentTable[i] = i;
}
long long totalCost = 0;
int numOfEdge = 0;
for (int i = 0; i < M; i++) {
// 같은 부모인지 체크
int nodeA = loadInfo[i][0];
int nodeB = loadInfo[i][1];
int cost = loadInfo[i][2];
if (checkSameParent(nodeA, nodeB))
continue;
Union(nodeA, nodeB);
totalCost += cost;
numOfEdge++;
//최소 신장트리 생성 완성 조건을 (엣지 갯수 == 노드 갯수 - 1)이 아닌,
// (엣지 갯수 == 노드 갯수 - 2)로 두면
// 자연스럽게 가장 비용이 높은 간선(신장트리에 포함될)을 제외하게 된다.
if (numOfEdge == N - 2)
break;
}
return totalCost;
}
int main() {
cin >> N >> M;
// 경로를 담을 벡터
for (int i = 0; i < M; i++) {
int a, b, cost;
cin >> a >> b >> cost;
loadInfo[i] = {a, b, cost };
}
// 최소 간선 비용 순으로 정렬
sort(loadInfo.begin(), loadInfo.begin() + M, compare);
long long answer = solution();
cout << answer << endl;
return 0;
}
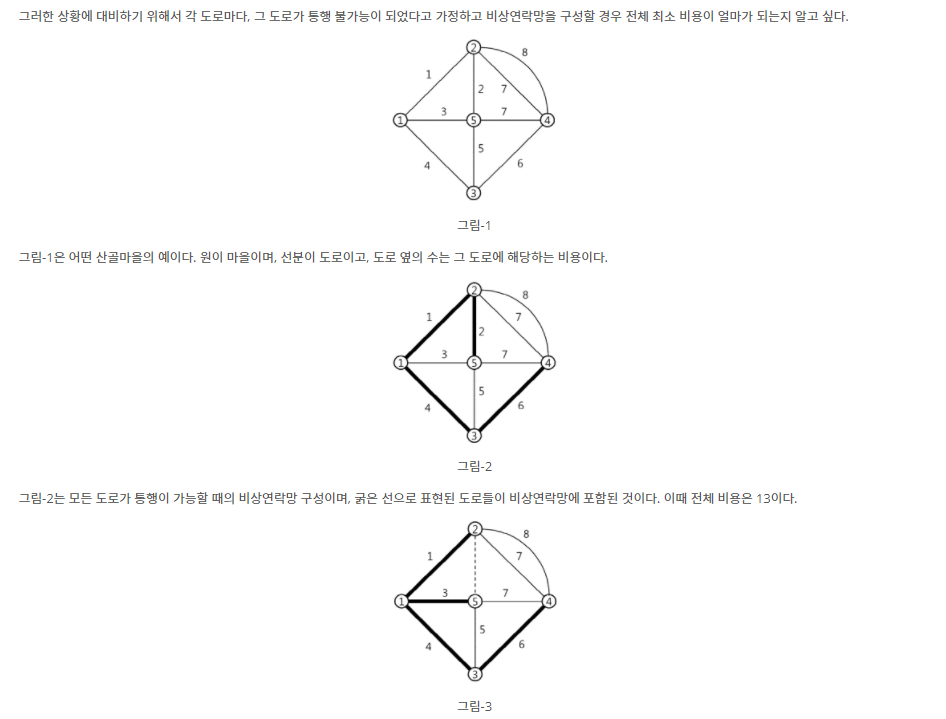
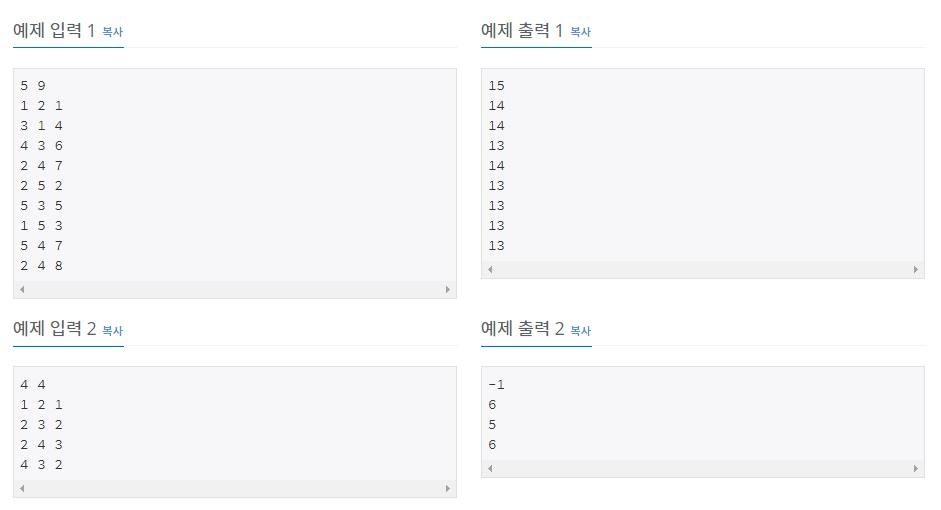
백준 - 안전한 비상연락망



#include <bits/stdc++.h>
using namespace std;
//
// 최소 신장트리와 크루스칼 알고리즘
//
// 간선의 비용에 따라 정렬을 먼저 해야한다. <= 크루스칼 알고리즘 전제 조건
bool compare(const vector<int>& a, const vector<int>& b) {
return a[3] < b[3]; // cost가 작은 순으로
}
int findParent(int node, vector<int>& parentTable) {
if (parentTable[node] == node)
return node;
else {
return parentTable[node] = findParent(parentTable[node], parentTable);
}
}
void unionEdge(int nodeA, int nodeB, vector<int>& parentTable) {
int nodeA_parent = findParent(nodeA, parentTable);
int nodeB_parent = findParent(nodeB, parentTable);
if (nodeA_parent < nodeB_parent)
parentTable[nodeB_parent] = parentTable[nodeA_parent];
else
parentTable[nodeA_parent] = parentTable[nodeB_parent];
}
long long solution(int exNum, const vector<vector<int>>& loadInfo, int numOfNode) {
// 유니온 파인드 활용
// 부모테이블 생성
vector<int> parentTable(numOfNode);
for (int i = 0; i < numOfNode; i++) {
parentTable[i] = i; // 초기에는 자신이 부모이다.
}
long long result = 0;
int numOfEdge = 0;
// 비용이 작은 순으로 간선을 하나씩 뽑는다.
for (int i = 0; i < loadInfo.size(); i++) {
int nowLoadNum = loadInfo[i][0];
if (nowLoadNum == exNum) {// 산사태가 일어난 간선이다.
//cout << "산사태가 일어난 " << nowLoadNum << "번 로드 제거" << '\n';
continue;
}
int nodeA = loadInfo[i][1];
int nodeB = loadInfo[i][2];
int cost = loadInfo[i][3];
// 유니온 연산으로 간선을 잇자!
// (1) 그전에 부모가 같은지 확인한다.
if (findParent(nodeA, parentTable) == findParent(nodeB, parentTable)) // 사이클 발생!
// 사이클이 발생했으므로 해당 간선은 무시한다.
continue;
// 부모가 다르다면 사이클x => 간선을 이어도 된다.
unionEdge(nodeA, nodeB, parentTable);
result += cost;
numOfEdge++;
if (numOfEdge == numOfNode - 1)
break;
}
if (numOfEdge != numOfNode - 1)
return -1;
else// if(numOfNode == numOfNode-1)
return result;
}
int main() {
int n, e;
cin >> n >> e;
// 간선 정보 받기
vector<vector<int>> loadInfo; // 간선 번호(0~e-1), 노드 a, 노드 b, 비용
for (int i = 0; i < e; i++) {
int a, b, cost;
cin >> a >> b >> cost;
loadInfo.push_back({ i, a - 1, b - 1, cost });
}
// (1) 비용에 따라 오름차순 정렬 => 비용이 적은 간선부터 뽑기 위함.
sort(loadInfo.begin(), loadInfo.end(), compare);
vector<long long> answers;
for (int i = 0; i < e; i++) { // O(300,000)
// 제외할 간선 번호
int execptNum = i;
long long answer = solution(execptNum, loadInfo, n); // O(300,000) <
answers.push_back(answer);
}
for (int i = 0; i < answers.size(); i++) {
cout << answers[i] << '\n';
}
}
N ≤ 5,000, M ≤ 20,000 이상의 제한이 있을 때엔 단순한 크루스칼 알고리즘으론 시간 조건 내에 해결할 수 없다.
