트리 / 이진트리 / 힙(완전 이진트리 기반)

이진트리(Binary Tree)

이진트리 특징

• 레벨 i에서의 노드의 최대 개수는 2^i개 (0 <= i)
• 높이가 h인 이진트리가 가질 수 있는 노드의 최소 갯수는 (h+1)개 (0 <= h)
• 높이가 h인 이진트리가 가질 수 있는 노드의 최대 갯수는 (2^(h+1)-1)개 (0 <= h)

이진트리 종류

1. 포화 이진트리(Full Binary Tree)

• 모든 레벨에 노드가 포화상태로 차 있는 이진트리
  
  source: https://sevity.tistory.com/141

1) 최대 노드 개수인 2^(h+1) - 1의 노드를 가진 이진트리
2) 루트 1번으로 하여 2^(h+1)-1까지 정해진 위치에 대한 노드 번호를 가진다.

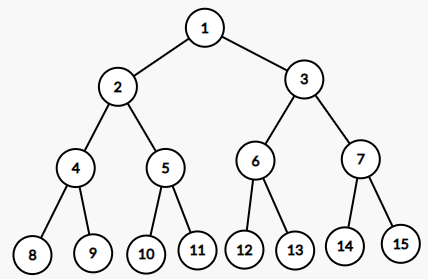
2. 완전 이진트리(Complete Binary Tree)

• 높이가 h이고 노드 수가 n개일 때 (단, h+1 <= n < 2^(h+1) -1), 포화 이진트리의 노드번호 1번부터 n번까지 빈 자리가 없는 이진트리
  
  source: https://jomuljomul.tistory.com/entry/%EC%99%84%EC%A0%84%EC%9D%B4%EC%A7%84%ED%8A%B8%EB%A6%ACComplete-Binary-Tree%EB%9E%80

3. 편향 이진트리(Skewed Binary Tree)

• 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드만을 가진 이진트리 (노드의 갯수: h+1개)
  
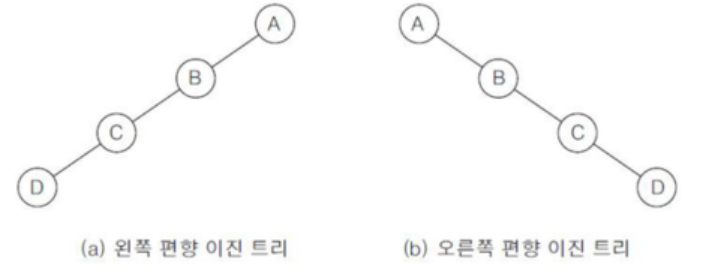
  source: https://itdexter.tistory.com/82

트리 표현 자료구조

1. 배열

1. 루트번호를 1로함
2. 레벨 n에 있는 노드에 대하여 왼쪽부터 오른쪽으로 2^n부터 2^(n+1)-1까지 번호를 차례대로 부여
   
   source: https://sevity.tistory.com/141

<노드 번호의 성질>

• 노드 번호가 i인 노드의 부모 노드 번호는 2로 나누 몫이다.
• 노드 번호가 i인 노드의 왼쪽 자식 노드 번호는 2*i
• "" 오른쪽 자식 노드 번호는 2*i + 1

배열을 이용한 이진트리 표현의 단점

• 메모리 공간 낭비 발생
  -> 편향 이진트리의 경우 사용하지 않는 배열 원소에 대한 메모리 공간 낭비 발생
• 노드가 자식 노드를 최대한 2개까지만 가질 수 있는 트리

2. 연결 리스트

• 연결 리스트를 통해 배열을 이용한 이진트리 표현의 단점을 보완한다.
• 이진트리의 모든 노드는 최대 2개의 자식 노드를 가지므로 일정한 구조의 단순한 연결 리스트 노드를 사용하여 구현할 수 있다.

class Node {
	int data; 
    Node* left;
    Node* right;
    ..
    ..
}

이진트리 특징

1. 탐색작업을 효율적으로 하기 위한 자료구조
2. 모든 원소는 서로 다른 유일한 키를 가짐
3. key(왼쪽 부트리) < key(루트 노드) < key(오른쪽 부트리)

source: https://junk-s.tistory.com/35

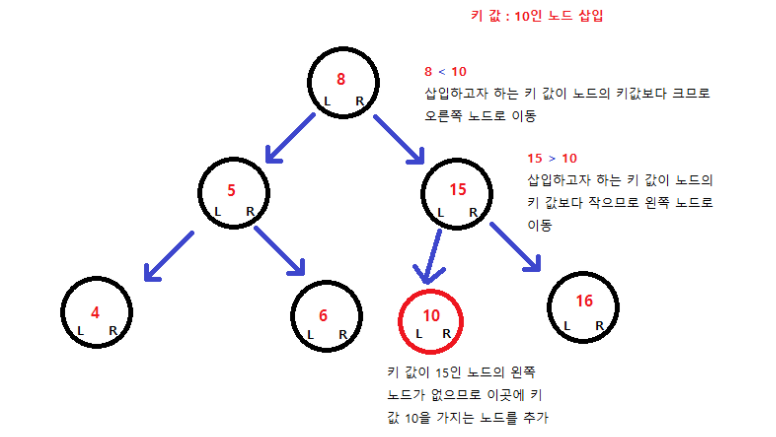
=> '중위순회'하면 오름차순으로 정렬된 값을 얻을 수 있다.

<탐색 연산>
1. 루트에서 시작
2. 탐색할 키값 x를 루트 노드의 키값과 비교
(2-1) 키값x == 루트 노드이 키값, 원하는 원소를 찾았으므로 탐색연산 성공
(2-2) 키값x < 루트 노드의 키값, 루트 노드의 왼쪽 서브트리에 대해서 탐색연산 수행
(2-3) 키값x > 루트 노드의 키값, 루트 노드의 오른쪽 부트리에 대해서 탐색연산 수행
3. 부트리에 대해서 순환적으로 탐색 연산을 반복

<삽입 연산>
1. 먼저 탐색 연산을 수행

• 삽입할 원소와 같은 원소가 트리에 있으면 삽입할 수 없으므로, 같은 원소가 트리에 있는지 탐색하여 확인
• 탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 됨.

2. 탐색 실패한 위치에 원소를 삽입
   
   

<삭제 연산>
1. 먼저 탐색 연산을 수행
2. 삭제 수행

(삭제할 노드가 단말 노드인 경우)
(2-1) 단말 노드의 부모 노드를 찾아서 연결 끊기.

(삭제할 노드가 하나의 서브트리만 가지고 있는 경우)
(2-2) 해당 노드를 삭제하고 서브 트리에서 삭제될 노드의 값과 가장 근사한 값을 갖는 노드를 서브 트리 루트로 설정한 후 부모 노드에 붙임.

(삭제할 노드가 두 개의 서브트리를 가지는 경우)
(2-3) 노드를 삭제하고 이를 대체하는 노드를 왼쪽 서브 트리의 가장 오른쪽 노드로 정하거나, 오른쪽 서브 트리의 가장 왼쪽 노르로 정하면 됨.

<<연산의 시간 복잡도>>
1. 탐색, 삽입, 삭제 시간은 트리의 높이에 좌우된다.
=> O(h), h: BST의 깊이(height)
2. 평균의 경우
=> 이진트리가 균형적으로 생성되어 있는 경우, O(logN)
3. 최악의 경우
=> 한쪽으로 치우친 경사 이진트리의 경우, O(n)
=> 순차 탐색과 시간복잡도가 같다.

<<검색 알고리즘의 비교>>
1. 배열에서의 순차 검색: O(n)
2. 정렬된 배열에서의 순차 검색: O(n)
3. 정렬된 배열에서의 이진탐색: O(logN)
-> 고정 배열 크기와 삽입, 삭제 시 추가 연산 필요
4. 이진탐색 트리에서의 평균: O(logN)
-> 최악의 경우: O(n)
-> 완전 이진트리 또는 균형 트리로 바꿀 수 있다면 최악의 경우를 없앨 수 있다.

---

힙(Heap)

• 완전 이진트리에 있는 노드 중에서 키값이 가장 큰 노드나 키값이 가장 작은 노드를 찾기 위해서 만든 자료구조

source: https://alloc.tistory.com/m/7

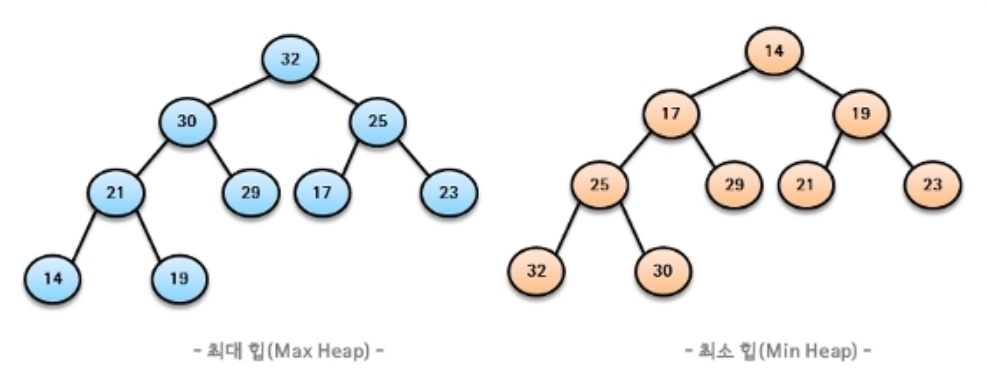
최대 힙(Max Heap)

• 키값이 가장 큰 노드를 찾기 위한 완전 이진트리
• 부모 노드의 키값 > 자식 노드의 키값
• 루트 노드: 키값이 가장 큰 노드

최소 힙(Min Heap)

• 키값이 가장 작은 노드를 찾기 위한 완전 이진트리
• 부모 노드의 키값 < 자식 노드의 키값
• 루트 노드: 키값이 가장 작은 노드

힙 연산

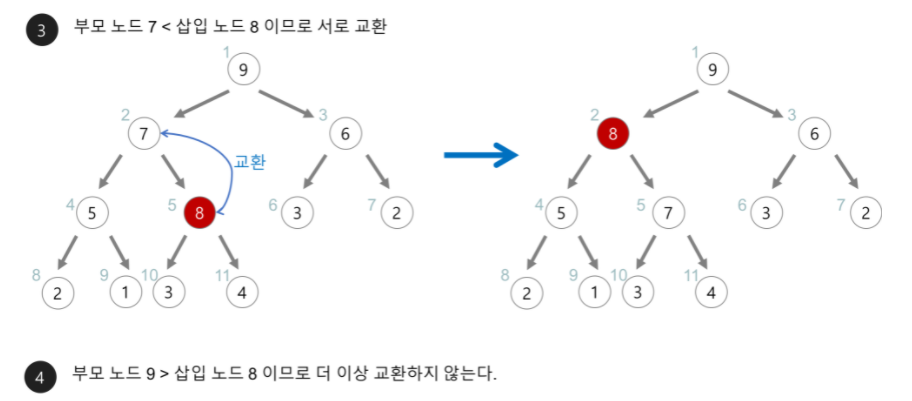
<삽입 연산> => O(logN)
1. 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 다음 위치에 이어서 삽입한다.
2. 새로운 노드를 부모 노드와 교환해나간다. 만약 교환이 불가능하면 그 위치에 자리잡는다.

source: https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

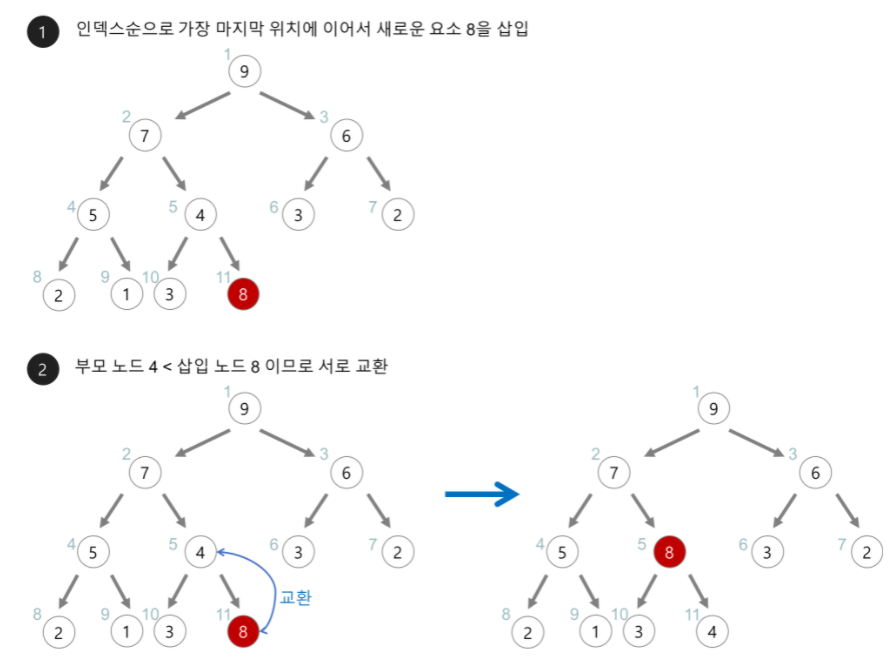
<삭제 연산> => O(logN)

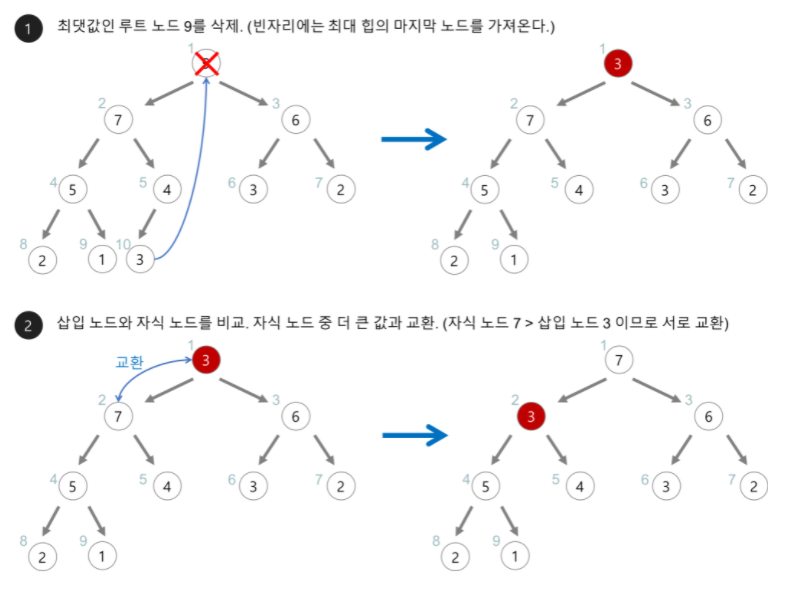
• 힙에서는 루트 노드의 원소만을 삭제할 수 있다.
• 루트 노드의 원소만을 삭제하여 반환
• 힙의 종류에 따라 최대값 또는 최소값을 구할 수 있다.
  => 이를 이용하여 우선순위 큐(priority_queue)를 구현할 수 있다.

1. 루트 노드의 원소를 삭제한다.
2. 마지막 노드를 루트 노드 위치로 이동시킨다.
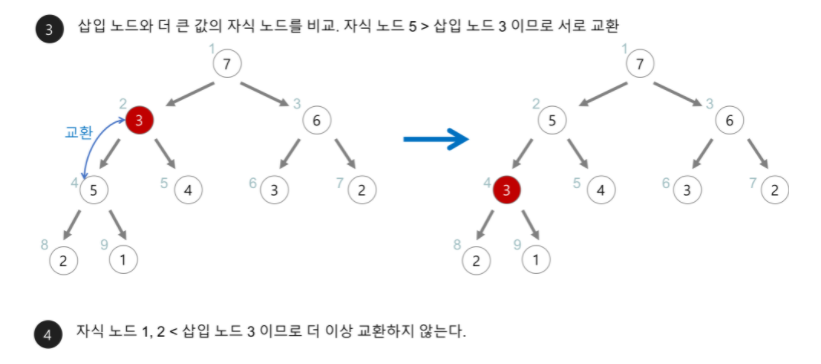
3. 삽입 노드와 자식 노드를 비교해가며 위치를 찾아간다.

source: https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html