reference: https://www.youtube.com/watch?v=_2DOKWvGets&list=PL-OC--HdIAXMXZ3IXSeLaO9Rl6qJNGc6g&index=33
구간 합 개념
구간 합 문제는 '값이 변경되지 않는 경우'와 '값이 변경되는 경우'로 크게 두 가지로 나뉠 수 있다.
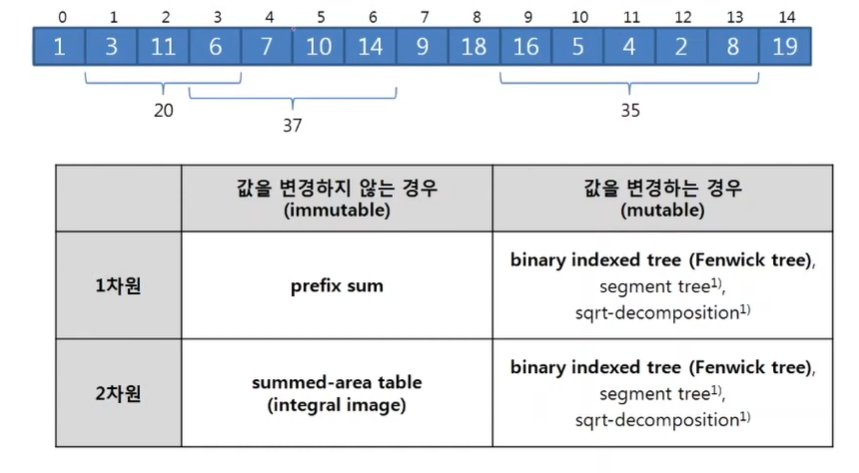
1차원 배열 | 값이 변하지 않는 경우 => prepix sum

예를 들어, 5번 인덱스부터 9번 인덱스까지의 합인 A[5] + A[6] + A[7] + A[8] + A[9]는 S[10] - S[5]로 계산할 수 있다.
sum 배열의 초기화 과정에서의 시간 복잡도는 O(n), 그리고 하나의 쿼리를 처리할 때의 시간 복잡도는 O(1)이 된다.
prepix sum 원리는 더하기 뿐 아니라 곱하기, XOR에도 동작 가능
A[5] * A[6] * A[7] * A[8] * A[9] = S[10] / S[5]
예제 문제1: Range Sum Query-Immutable _ leetCode
source: https://leetcode.com/problems/range-sum-query-immutable/

class NumArray {
public:
vector<int> S;
NumArray(vector<int>& nums) {
S.resize(nums.size() + 1);
for(int i=0; i<nums.size(); i++){
S[i+1] = S[i] + nums[i];
}
}
int sumRange(int left, int right) {
return S[right+1] - S[left];
}
};예제 문제2: 두 배열의 합_백준 (+ 이진탐색)
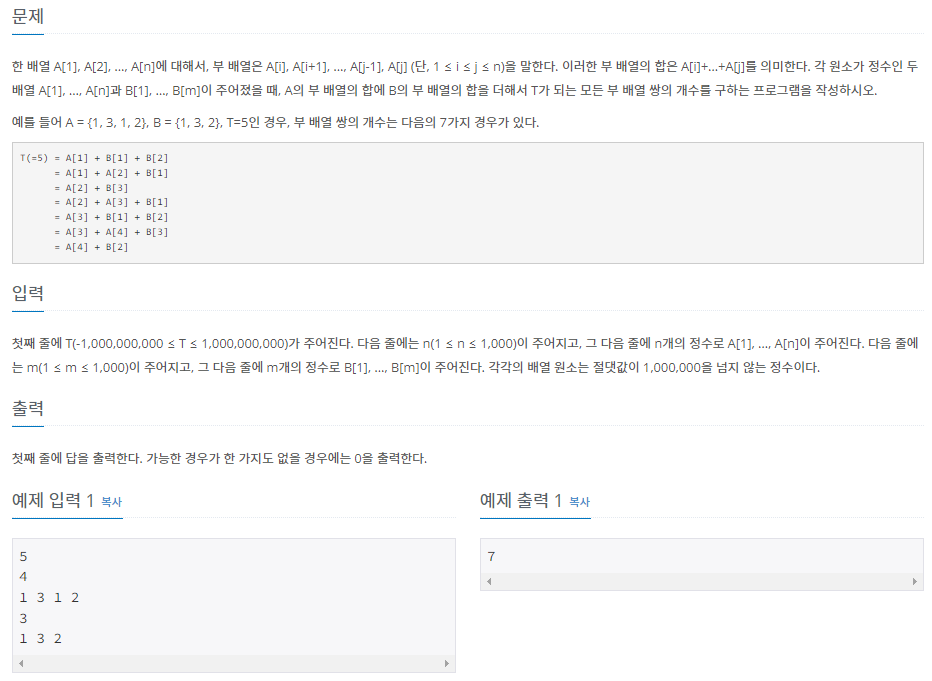
먼저 배열 A의 sum table인 ASum과 배열 B의 sum table인 BSum을 만들었다.
그리고 배열 A의 모든 구간합 케이스 각각을 특정 배열 B의 구간합과 더하고, 이를 N(문제에선 T)와 비교하였다.
배열 A의 구간합을 구하는 것은 이중 for문으로, 이중 for문 안에서 배열 B의 구간합 케이스(정렬됨)를 이진탐색으로 탐색하여 합이 N이 되는 것을 찾았다.
따라서 시간 복잡도는 O(N^2)*O(logN)이다.
#include <vector>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
int N, AN, BN;
vector<int> A(1000);
vector<int> B(1000);
long long solution() {
long long answer = 0;
// 1) A의 구간합 구하기
vector<int> ASum(AN + 1, 0);
for (int i = 0; i < AN; i++) {
ASum[i + 1] = ASum[i] + A[i];
}
// 2) B의 구간합 구하기
vector<int> BSum(BN + 1, 0);
for (int i = 0; i < BN; i++) {
BSum[i + 1] = BSum[i] + B[i];
}
// 3) B의 모든 구간합 케이스를 만든다. <= O(n)
vector<int> AllBSumCase;
for (int i = 1; i <= BN; i++) {
for (int j = 0; j < i; j++) {
AllBSumCase.push_back(BSum[i] - BSum[j]);
}
}
// 이분탐색을 위해 정렬
sort(AllBSumCase.begin(), AllBSumCase.end()); // <= O(nlogn)
vector<int> countVec(AllBSumCase.size(), 0);
countVec[0] = 1;
int prev = AllBSumCase[0];
for (int i = 1; i < AllBSumCase.size(); i++) {
if (AllBSumCase[i] == prev) {
countVec[i] = countVec[i - 1] + 1;
}
else {
countVec[i] = 1;
}
prev = AllBSumCase[i];
}
// AllBSumCase에 중복되는 요소가 있을 수 있다.
// 그 이유는 배열 B 요소에 음수가 있을 수 있기 때문이다.
// 이에 이진탐색 과정 중 탐색을 줄이기 위해 해당 구간합이 몇 개가 있는지를 담는 자료구조를 추가로 구현한다.
unordered_map<int, int> um; // <sum 값, 해당 값의 갯수>
for (int i = 0; i < AllBSumCase.size(); i++) { // <= O(nlogn)
// AllBSumCase.size() == BN^2 (~1,000,000)
um[AllBSumCase[i]] = countVec[i];
}
// cf) A[x] + A[x+1} + .. + .. + A[y] = ASum[y+1] - ASum[x]
// A의 구간합에 따라 더하면 정답인 B 구간합을 찾기 <= 이진탐색
for (int i = 1; i <= AN; i++) { // <= O(n^2*logn)
for (int j = 0; j < i; j++) {
int aRangeSum = ASum[i] - ASum[j];
// 배열 요소에 음수를 포함하므로 이 statement는 생략되어야 한다.
//if (aRangeSum >= N)
// continue;
int start = 0;
int end = AllBSumCase.size() - 1;
while (start <= end) {
int pivot = (start + end) / 2;
if (aRangeSum + AllBSumCase[pivot] == N) {
answer += um.at(AllBSumCase[pivot]);
break;
}
else if (aRangeSum + AllBSumCase[pivot] < N)
start = pivot + 1;
else
end = pivot - 1;
}
}
}
return answer;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> N;
cin >> AN;
for (int i = 0; i < AN; i++) {
cin >> A[i];
}
cin >> BN;
for (int i = 0; i < BN; i++) {
cin >> B[i];
}
long long answer = solution();
cout << answer << endl;
}예제 문제3: 구간 합 구하기 5_백준
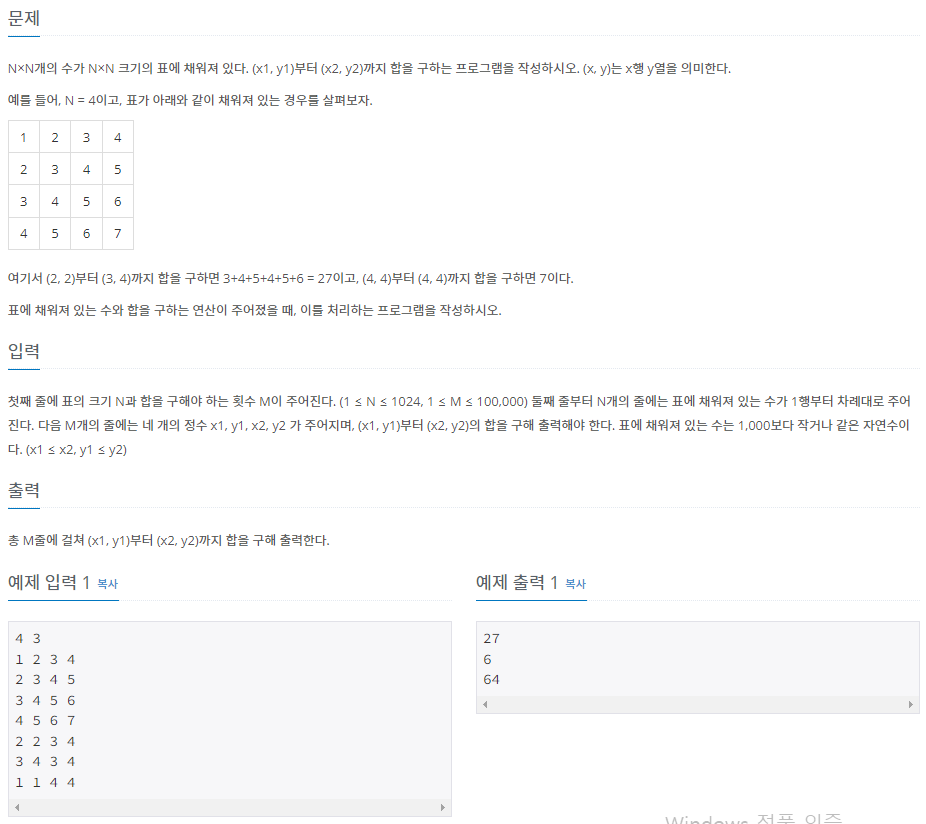
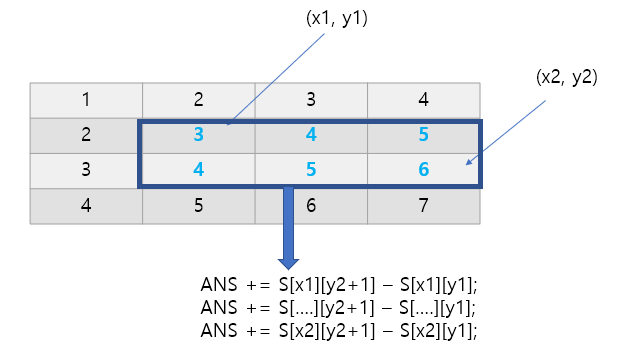
#include <iostream>
#include <vector>
using namespace std;
int N, M;
vector<vector<int>> MAP(1024, vector<int>(1024));
vector<vector<int>> RangeSum(1024, vector<int>(1024 + 1, 0));
void makeRangeSum() {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
RangeSum[i][j+1] = RangeSum[i][j] + MAP[i][j];
}
}
}
int solution(pair<pair<int, int>, pair<int, int>>& q) {
int x1 = q.first.first;
int y1 = q.first.second;
int x2 = q.second.first;
int y2 = q.second.second;
int answer = 0;
for (int i = x1; i <= x2; i++) {
// y1~y2의 구간합 = RangeSum[][y2+1] - RangeSum[][y1]
answer += RangeSum[i][y2 + 1] - RangeSum[i][y1];
}
return answer;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N >> M;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cin >> MAP[i][j];
}
}
vector < pair<pair<int, int>, pair<int, int>>> queries(M);
for (int i = 0; i < M; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
// 범위 조절
queries[i] = { {x1-1, y1-1}, {x2-1, y2-1} };
}
// 구간합을 담은 자료구조(전역)를 미리 만들어 놓은 후 쿼리를 수행한다.
makeRangeSum(); // <= O(N^2)
vector<int> answers(M);
for (int i = 0; i < M; i++) {
int answer = solution(queries[i]);
answers[i] = answer;
}
for (int i = 0; i < M; i++) { // <= O(M * N)
cout << answers[i] << '\n';
}
return 0;
}1차원 배열 | 값이 변하는 경우 => Binary Indexed Tree (Fenwick Tree)

BIT 자료구조는 물리적으로 O(n)의 메모리 공간을 가진다.
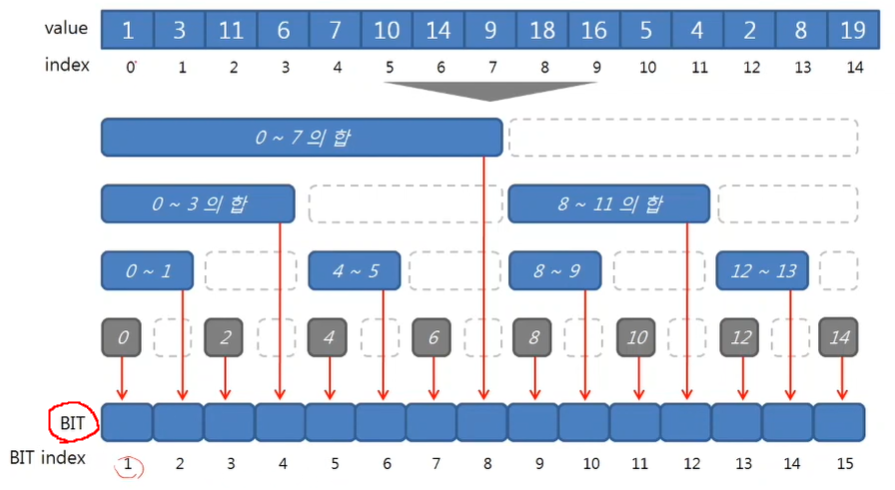
Range sum
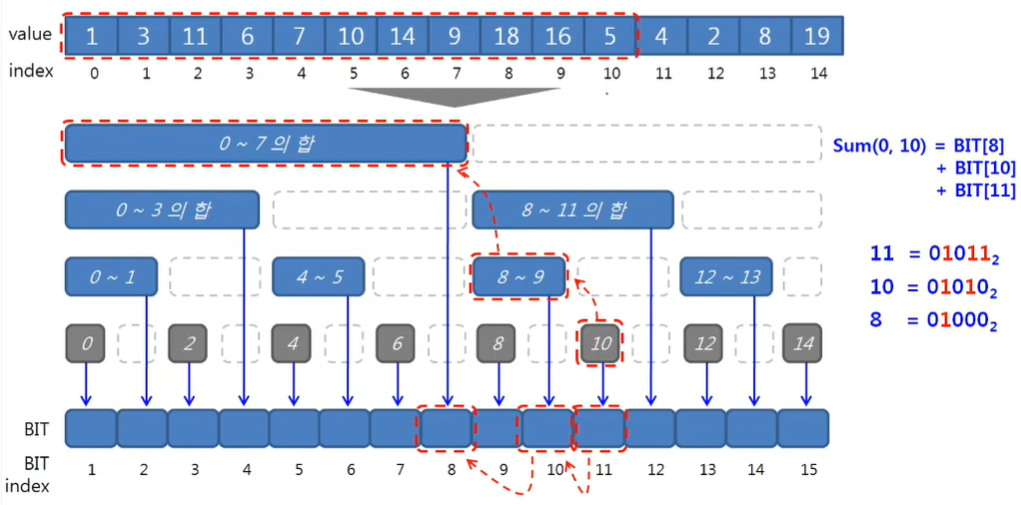
인덱스 0부터 인덱스 10까지의 합인 SUM(0, 10)은 다음과 같이 구할 수 있다.
SUM(0, 10) = BIT[11] + BIT[10] + BIT[8]
그렇다면 11, 10, 8이란 BIT 배열의 인덱스는 어떻게 찾을까?
먼저 SUM(0, 10)에서 10의 다음 숫자인 11은 비트 표현으로 다음과 같이 표기될 수 있다.
11(10) = 01011(2)
그리고 비트의 작은 자리부터 1을 제거해나간다.
10(10) = 01010(2)
8(10) = 01000(2)
0(10) = 00000(2)
Update
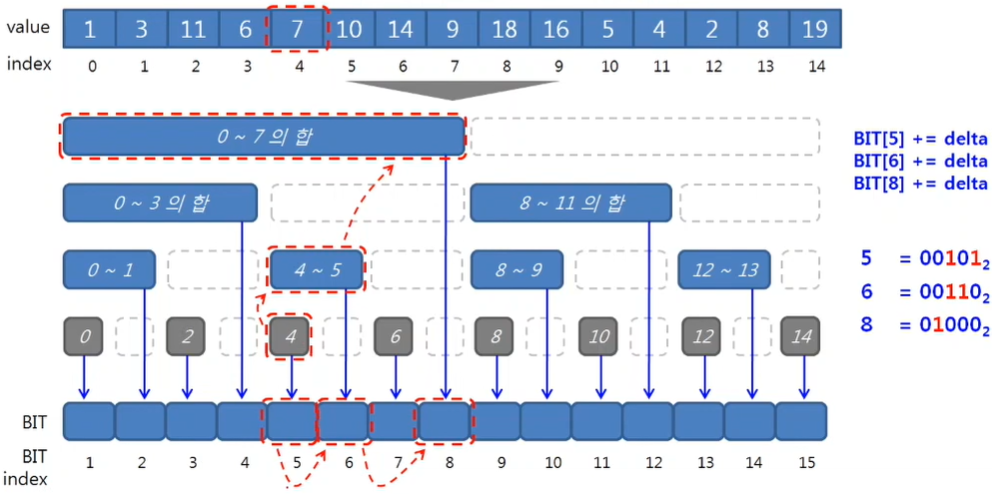
원래 배열에 인덱스 4번의 요소의 값이 변경되었다. 그렇다면 BIT 배열을 어떻게 바꿀 수 있을까? 아래와 같이 BIT 배열이 변경된다.
BIT[5] += delta
BIT[6] += delta
BIT[8] += delta여기서 5, 6, 7은 아래와 같이 구할 수 있다.
먼저 4의 다음 숫자인 비트 표현으로 아래와 같이 나타낼 수 있다.
5(10) = 00101(2)
그리고 마지막 1이 있는 비트에 1씩 더해나간다.
6(10) = 00101(2) + 00001(2) = 00110(2)
8(10) = 00110(2) + 00010(2) = 01000(2)
16(10) = 01000(2) + 01000(2) = 10000(2)
업데이트, 쿼리에서의 시간 복잡도는 둘 다 O(logN)이다.
템플릿 코드
struct BinaryIndexedTree {
vector<int> BIT;
BinaryIndexedTree(int n) {
BIT.resize(n + 1, 0);
}
void initBIT(const vector<int>& v) {
for (int i = 0; i < v.size(); i++) {
addToBIT(i, v[i]);
}
}
private:
// 원래 배열의 pos 인덱스에 delta만큼 가산
// 이때 BIT를 갱신하기
void addToBIT(int pos, int delta) {
// BIT의 인덱스로
pos++;
while (pos < BIT.size()) {
BIT[pos] += delta;
pos += pos & (-pos); // 최하위 bit에 1을 더함
}
}
int sum(int pos) {
// BIT 인덱스로
pos++;
int sum = 0;
while (pos > 0) {
sum += BIT[pos];
pos &= (pos - 1); // 최하위 bit clear
}
return sum;
}
int rangeSum(int left, int right) {
int rSum = sum(right);
if (left > 0)
rSum -= sum(left -1);
return rSum;
}
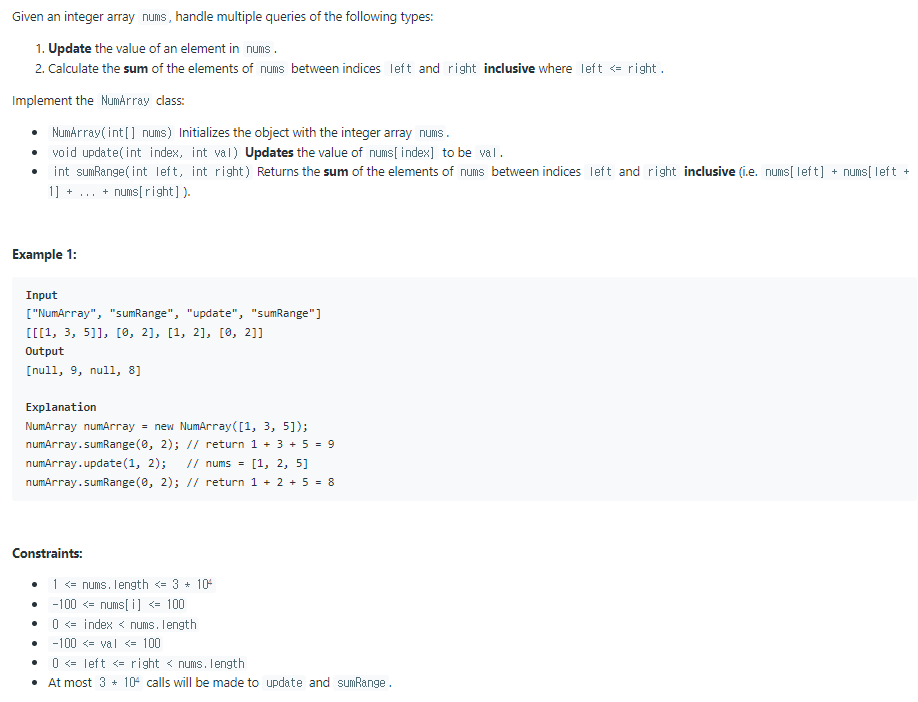
};예제 문제: Range Sum Query-Mutable _ leetCode
source: https://leetcode.com/problems/range-sum-query-mutable/
class BIT {
private:
vector<int> Tree;
public:
BIT(int n){
Tree.resize(n+1, 0);
}
void initBIT(const vector<int>& v){
for(int i=0; i<v.size(); i++){
addToBIT(i, v[i]);
}
}
void addToBIT(int pos, int delta){
pos++;
while(pos < Tree.size()){
Tree[pos] += delta;
pos += pos & (-pos);
}
}
int rangeSum(int left, int right){
int rSum = sum(right);
if(left > 0)
rSum -= sum(left-1);
return rSum;
}
private:
int sum(int pos){
pos++;
int sum = 0;
while(pos > 0){
sum += Tree[pos];
pos &= (pos - 1);
}
return sum;
}
};
class NumArray {
public:
BIT* bitree;
vector<int> nums;
NumArray(vector<int>& nums) {
bitree = new BIT(nums.size());
(*bitree).initBIT(nums);
this->nums = nums;
}
void update(int index, int val) {
int delta = val - nums[index];
(*bitree).addToBIT(index, delta);
nums[index] = val;
}
int sumRange(int left, int right) {
return (*bitree).rangeSum(left, right);
}
~NumArray(){
delete bitree;
}
};

