백트래킹 - N과 M (백준)

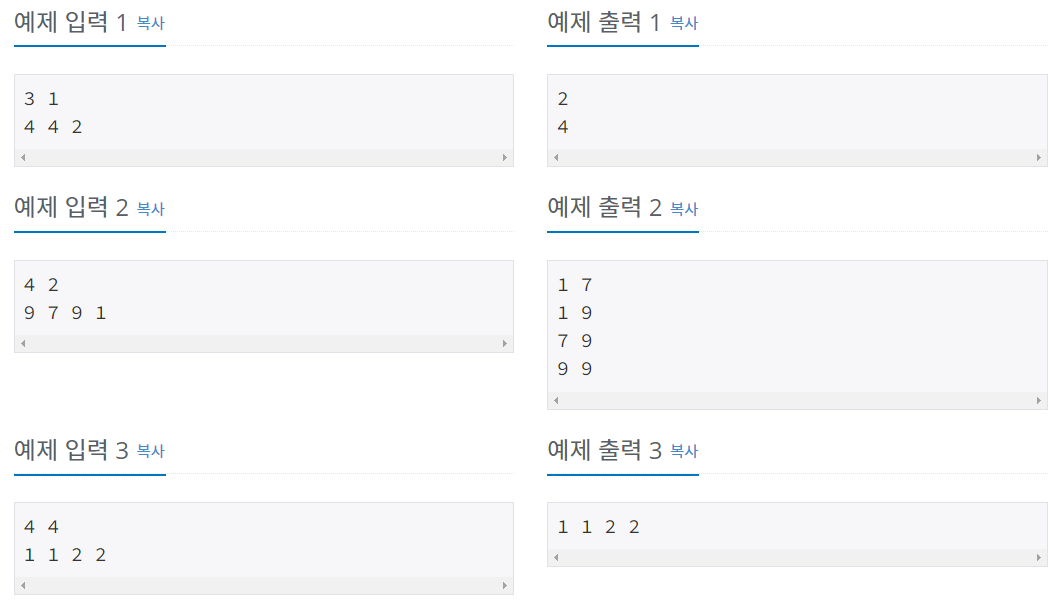
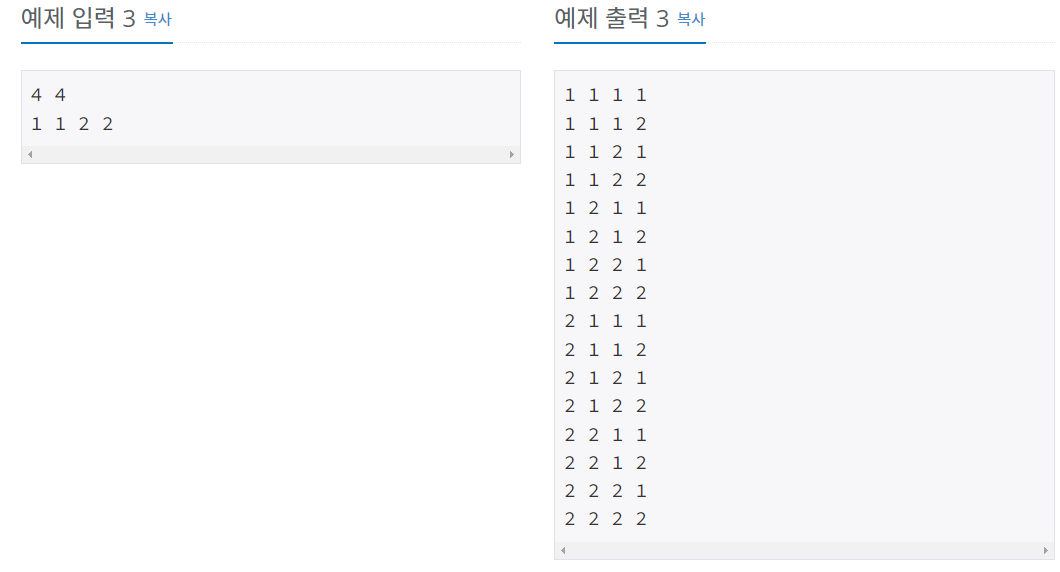
백트래킹 = DFS(탐색) + 조건문을 통한 가지치기 => 효율적인 탐색

dfs + 메모제이션도 일종의 백트래킹이라 볼 수 있을 듯.

---

N과 M 기본

N과 M(1): 백트래킹

#include <bits/stdc++.h>
using namespace std;

int n, m;
int answer[8+1];
bool check[8+1];

void dfs(int len) {
	// 종료조건
	if (len == m) {
		// 출력
		for (int i = 1; i <= m; i++) {
			cout << answer[i] << ' ';
		}
		cout << '\n';
		return;
	}

	// 탐색
	for (int i = 1; i <= n; i++) {
		// 다음 후보
		int cand = i;

		// 조건문(백트레킹)
		if (check[cand] == true)
			continue;	// 가지치기 => 더 탐색하지 않고 백트래킹 => 다른 후보 탐색
		
		// 재귀
		check[cand] = true;		// visited
		answer[len + 1] = cand;
		dfs(len + 1);
		check[cand] = false;	// 복구

	}
}

int main() {
	cin >> n >> m;

	dfs(0);
	
	return 0;
}

N과 M(2): for문의 시작점을 조절하는 것이 일종의 백트래킹?

#include <bits/stdc++.h>
using namespace std;

int n, m;
vector<int> ans(8);

void dfs(int count, int before){
    // 종료조건
    if(count == m){
        for(int i=0; i<m; i++){
            cout << ans[i] << ' ';
        }
        cout << '\n';

        return;
    }

	// for문 시작점 control
    for(int i=before+1; i<=n; i++){
        ans[count] = i;
        dfs(count+1, i);
        // 항상 이전에 선택한 인덱스 다음부터 탐색하니 visited 처리는 필요없음. 
    }
}

int main(){
    cin >> n >> m;

    dfs(0, 0);

    return 0;
}

N과 N(3): 백트래킹 필요없이 싹 다 출력

#include <bits/stdc++.h>
using namespace std;

int n, m;
int answer[8+1];
bool check[8+1];

void dfs(int len) {
	// 종료조건
	if (len == m) {
		// 출력
		for (int i = 1; i <= m; i++) {
			cout << answer[i] << ' ';
		}
		cout << '\n';
		return;
	}

	// 재귀
	for (int i = 1; i <= n; i++) {
		// 다음 후보
		int cand = i;

		// // 조건문(백트레킹)
		// if (check[cand] == true)
		// 	continue;	// 가지치기 => 더 탐색하지 않고 백트래킹 => 다른 후보 탐색
		
		// 깊이 탐색
		//check[cand] = true;
		answer[len + 1] = cand;
		dfs(len + 1);
		//check[cand] = false;	

	}
}

int main() {
	cin >> n >> m;

	dfs(0);
	
	return 0;
}

N과 M의 범위는 <= 7 까지이다. 따라서 시간복잡도는 최대 O(7^7)

---

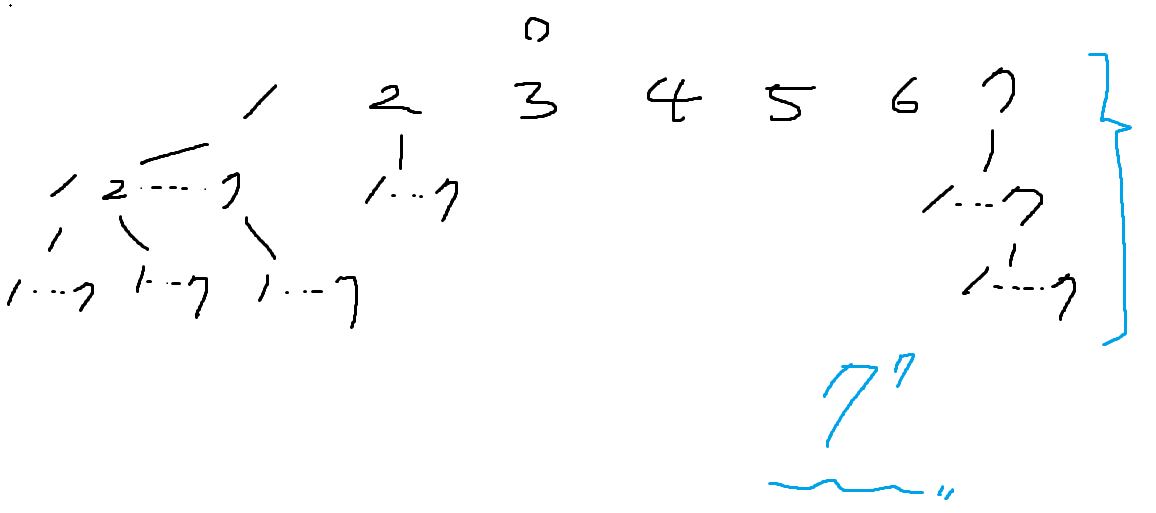
N과 M 심화(10~12)

N과 M(10): 비내림차순 + 중복되는 입력 값 존재

테스트케이스 예제

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;


void dfs_with_BT(int idx, vector<int>& vec, vector<int>& result, int len, int maximum) {
	// 종료조건
	if (len == maximum) {
		for (int i = 0; i < len; i++) {
			cout << result[i] << ' ';
		}
		cout << endl;
		return;
	}

	// 탐색
	// 같은 레벨에서 중복된 같이 선택되면 안된다.
	int beforeValue = -1;
   	// 루프의 범위를 좁히는 방식(i=idx 시작~)으로 가지치기
	for (int i = idx; i < vec.size(); i++) {
		int nowValue = vec[i];
		int nowIdx = i;
		
		// prev 설정을 통한 가지치기
		if (nowValue == beforeValue)
			continue;
		else {

			beforeValue = nowValue;
			result.push_back(nowValue);
			// 재귀
			dfs_with_BT(nowIdx + 1, vec, result, len + 1, maximum);
			// 복구
			result.pop_back();
		}
	}

}

int main() {
	int n, m;
	cin >> n >> m;

	vector<int> vec(n);
	for (int i = 0; i < n; i++) {
		int x;
		cin >> x;
		vec[i] = x;
	}

	// 오름차순 정렬
	sort(vec.begin(), vec.end());

	vector<int> temp;
	dfs_with_BT(0, vec, temp, 0, m);
	
	return 0;
}

N과 M(11): 같은 수 여러 번 고르기 가능 + 중복되는 입력 값 존재

테스트케이스 예제

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;


void dfs_with_BT(vector<int>& vec, vector<int>& result, int len, int maximum) {
	// 종료조건
	if (len == maximum) {
		for (int i = 0; i < len; i++) {
			cout << result[i] << ' ';
		}
		cout << '\n';
		return;
	}

	// 탐색
	// 같은 레벨에서 중복된 값이 선택되면 안된다.
	int beforeValue = -1;


	int vecLen = vec.size();	// 시간초과를 막은 함수 호출 최소화


	for (int i = 0; i < vecLen; i++) {
		int nowValue = vec[i];
		int nowIdx = i;

		// 백트레킹
		if (nowValue == beforeValue)
			continue;
		else {

			beforeValue = nowValue;
			//result.push_back(nowValue);
			// 시간초과로 변경
			result[len] = nowValue;
			// 재귀
			dfs_with_BT(vec, result, len + 1, maximum);
			// 복구
			//result.pop_back();
		}
	}

}

int main() {
	// C++ 입출력 속도 올리기
	//ios_base::sync_with_stdio(false);
	//cin.tie(NULL);
	//cout.tie(NULL);

	int n, m;
	cin >> n >> m;

	vector<int> vec(n);
	for (int i = 0; i < n; i++) {
		int x;
		cin >> x;
		vec[i] = x;
	}

	// 오름차순 정렬
	sort(vec.begin(), vec.end());

	vector<int> temp(m);
	dfs_with_BT(vec, temp, 0, m);

	return 0;
}

N과 M(12): 같은 수 여러 번 고르기 가능 + 비내림차순

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int N, M;
vector<int> arr(8);

void DFS(int idx, vector<int>& answer) {
	// 종료조건
	if (answer.size() == M) {
		for (int i = 0; i < M; i++) {
			cout << answer[i] << " ";
		}
		cout << '\n';
		return;
	}

	// 탐색
	int prev = -1;
	for (int i = idx; i < N; i++) {
		int nowIdx = i;

		if (arr[nowIdx] == prev)
			continue;

		answer.push_back(arr[nowIdx]);
		DFS(nowIdx, answer);
		answer.pop_back();
		prev = arr[nowIdx];
	}
}

void solution() {
	// (1) 정렬
	sort(arr.begin(), arr.begin() + N);

	// (2) DFS
	vector<int> temp;
	DFS(0, temp);
}

int main() {
	cin >> N >> M;
	for (int i = 0; i < N; i++) {
		cin >> arr[i];
	}

	solution();
}