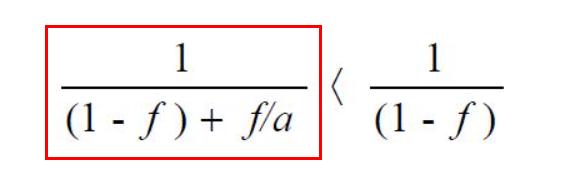reference: "프로그래머가 몰랐던 멀티코어 CPU 이야기" / 김민장, "Computer System A Programmers'Perspective" / 랜달 E.브라이언트
암달의 법칙
컴퓨터 공학 전반에 적용할 수 있는 중요한 개념.
문제 예시
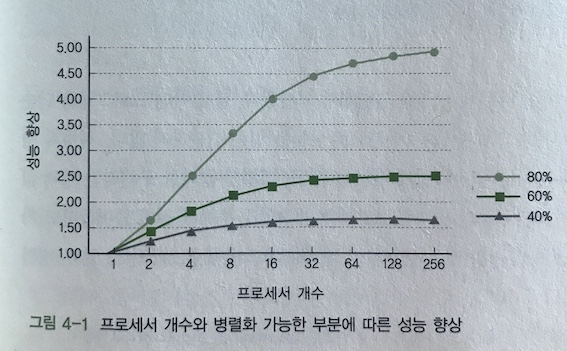
프로그램을 분석해보니 80%의 부분을 병렬화할 수 있음을 알아냄. 프로세서가 2개, 4개, 8개, 16개일 때 성능은?
전체 프로그램 수행 시간 1 중 0.8을 프로세서 N개로 완벽히 병렬 처리할 수 있다면,
총 수행시간 = 0.8/N(병렬화) + 0.2(직렬 수행)
극단적으로 양자화 컴퓨터의 힘을 빌어 무한히 병렬화한다 하더라도 프로그램의 수행 시간은 0.2가 극한 값이 될 것.
따라서 병렬화 가능 부분이 80%라면 최대 얻을 수 있는 성능 향승은 5배가 한계 값.
f: 병령화 가능한 부분의 비율, a: 프로세서 개수
프로세서 a가 완벽하게 f 만큼의 일을 병렬 처리한다는 매우 이상적인 가정을 하고 있음.
위의 예라면,
1 / ( (1-0.8) + 0.8/N) ) = (N->무한대) 1 / 0.2, 최대 5배 성능 향상
프로그램 중 40%만 병렬화가 가능하다면 아무리 많은 프로세서가 있다한들 성능 향상은 채 2배도 될 수 없음.
80% 이상 병렬화 할 수 있다한들 성능을 5배 이상 향상시킬 수 없음.
(source: https://johngrib.github.io/wiki/amdahl-s-law/)
병렬화 가능한 부분을 효율적으로 병렬화(N의 갯수 늘이기)하여 최적의 성능을 얻는 것도 중요하지만,
무엇보다 병렬화 가능한 부분을 극대화, 다시 말해 직렬로 처리해야 하는 부분(1-f)를 줄이는 것이 핵심이다(병렬화 가능 부분 늘이기).
과학이나 수학 관련 프로그램은 수행 시간의 대부분을 순환문이 차지하며 병렬 가능한 경우가 많다. 어떤 경우는 완벽히 병렬화 가능(어떠한 뮤텍스나 동기화도 필요없이)하기도 하고 어떤 때는 동기화가 필요하기도 하다. 어찌 되었든 수행 시간의 대부분이 병렬화로 도움을 얻을 수 있다.
암달의 법칙 제한
암달의 법칙은 사실 너무 많은 것을 간단하게 가정. 실제 어떤 프로그램을 단순히 병렬 가능한 부분과 그렇지 않은 부분으로 나누는 일은 간단하지 않음. 직렬과 병렬 실행 가능한 부분이 혼재되어 있기 때문. 또 병렬성에 대한 구체적인 정의 없이 단순히 병렬 가능한 부분이 완벽히 프로세서 개수만큼 수행 시간이 줄어든다고 가정한다. (주어진 작업이 별 노력 없이 완벽히 병렬화 가능할 때, 이를 embarrassingly parallel이라고 부른다.)
실제 병렬화 후 얻어지는 성능은 사실 이보다 크게 낮을 가능성도 있다.
병렬화에는 쓰레드 생성 비용 같은 고정 비용이 들어가고 프로세스/스레드 사이에 뮤텍스 같은 동기화 객체로 효율이 떨어지게 되므로 실제로 성능이 그리 많이 향상되지 않을 수 있다. 따라서 암달의 법칙에는 제한이 많음.
정리하자면, (1) 병렬화 가능 부분을 정확히 나누는 것이 어렵다. (2) 병렬화 가능 부분도 추가 비용이 들어가기에 비례적인 성능 향상이 어려움.