[유니온-파인드] 개념과 예제 문제

source: "이겻이 코딩테스트 이것이 취업을 위한 코딩 테스트다 with 파이썬" / 나동빈

유니온-파인드 자료구조/알고리즘

서로소 집합: 공통 원소가 없는 두 집합
ex) 집합{1, 2}, 집합{3, 4}는 서로소 관계. {1, 2}, {2, 3}은 서로소 관계 아님.

서로소 집합 자료구조는 합집합(union)과 찾기(find) 연산으로 구성됨. 이는 스택, 큐 자료구조가 각각 push, pop 연산을 제공하는 것과 같다.
이에 따라 서로소 집합 자료구조는 유니온-파인드 자료구조라 불리기도 함.

source: https://travelbeeee.tistory.com/369

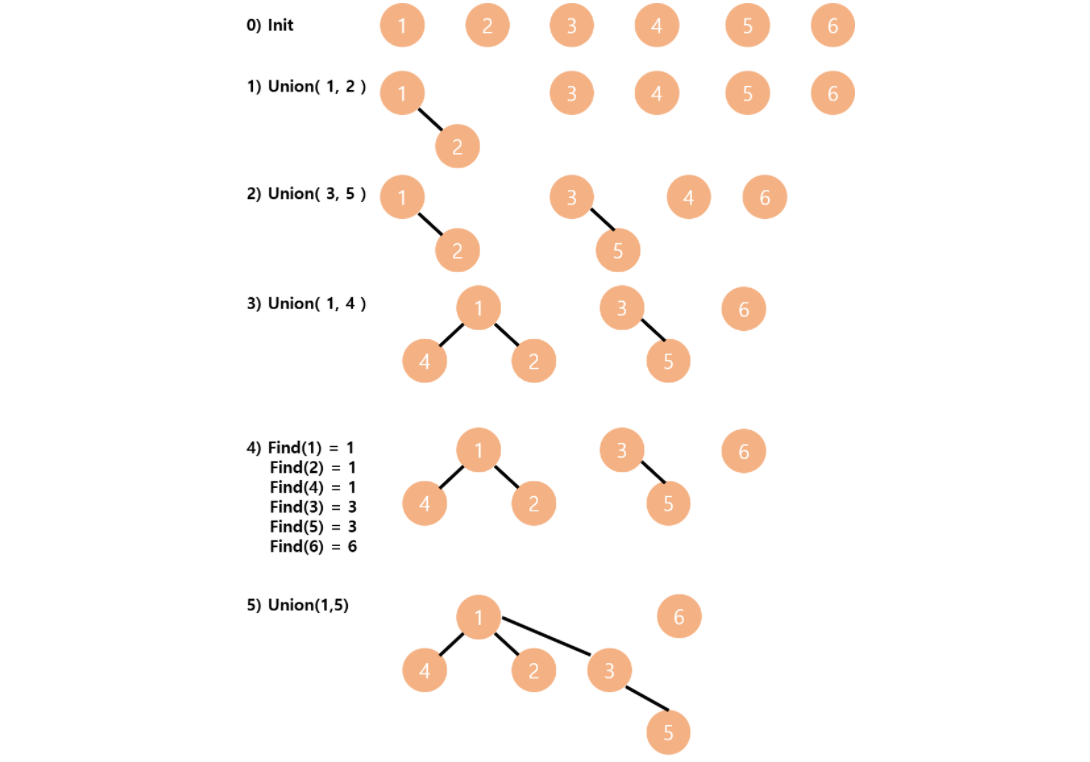
유니온(Union) 연산과 그래프

유니온 연산은 그래프 형태로 표현될 수 있다. 각 원소는 그래프의 노드로 표현되고, 유니온 연산은 두 원소 간의 간선을 잇는 것으로 생각할 수 있다.
그리고 이 그래프를 통해 각 원소의 집합 정보를 표현하려면 트리 자료구조를 이용해야 하고, 트리 구조 상 번호가 작은 노드가 부모, 번호가 큰 노드가 자식으로 하여 만든 트리가 유니온-파인드 연산으로 만들어 낸 부모 테이블이라 볼 수 있다.

경로 압축

find 함수를 재귀적으로 호출한 뒤 부모 테이블 값을 갱신하는 기법. 이를 통해 find 함수 인자로 전달된 노드의 루트 노드가 바로 부모 노드가 되어 이 후 동일한 노드에 find 함수 호출 시 루트 노드에 더욱 빠르게 접근할 수 있다.

// FindParent
int findParent(int node) {
	if (parentTable[node] == node)
		return parentTable[node];
	else
		//return findParent(parentTable[node]);
        return parentTable[node] = findParent(parentTable[node]);
}

---

템플릿 소스 코드

#include <bits/stdc++.h>
using namespace std;

class UnionFind{
private:
	int n;
	vector<int> *parentTablePointer;
	vector<int> parentTable;

public:
	UnionFind(int n) {
		// n은 노드의 수 
		this->n = n;
		parentTablePointer = new vector<int>(n+1);
		parentTable = *parentTablePointer;

		// parentTable 초기화
		for (int i = 1; i <= n; i++) {
			parentTable[i] = i;
		}
	}

	~UnionFind() {
		parentTablePointer->clear();
	}

	// FindParent
	int findParent(int node) {
		if (parentTable[node] == node)
			return parentTable[node];
		else
			//return findParent(parentTable[node]);
            return parentTable[node] = findParent(parentTable[node]);
	}

	// Union
	void unionFunc(int a, int b) {
		int a_parent = findParent(parentTable[a]);
		int b_parent = findParent(parentTable[b]);
		if (a_parent < b_parent)
			// parentTable[b] = a_parent; <= (X)
            parentTable[b_parent] = a_parent;
		else
			// parentTable[a] = b_parent; <= (X)
            parentTable[a_parent] = b_parent;
	}

	void showSet() {
		for (int i = 1; i <= n; i++) {
			cout << findParent(i) << ' ';
		}
		cout << '\n';
	}

	void showParentTable() {
		for (int i = 1; i <= n; i++) {
			cout << parentTable[i] << ' ';
		}
		cout << '\n';
	}
};

int main() {

	int n, e;		// 노드의 갯수: n, 연결관계 갯수: e
	cin >> n >> e;

	// 서로소 집합 자료구조(유니온-파인드 자료구조)
	UnionFind uf(n);

	for (int i = 0; i < e; i++) {
		int a, b;
		cin >> a >> b;
        
          	// Union 연산!	
		uf.unionFunc(a, b);
	}

	uf.showSet();
	uf.showParentTable();

}

(입력)
6 4
1 4
2 3
2 4
5 6

(출력)
1 1 1 1 5 5 <= 각 원소가 속한 집합
1 1 2 1 5 5 <= 부모 테이블

추가로 재귀의 호출을 최소화시키는 기법 사용시
(출력)
1 1 1 1 5 5
1 1 1 1 5 5

---

※ 이전 나의 실수

void unionFunc(int a, int b) {
	int a_parent = findParent(parentTable[a]);
	int b_parent = findParent(parentTable[b]);
	if (a_parent < b_parent)
		// parentTable[b] = a_parent; <= (X)
          	parentTable[b_parent] = a_parent;
	else
		// parentTable[a] = b_parent; <= (X)
          	parentTable[a_parent] = b_parent;
}

만약 단순히 parentTable[a] = b_parent; 라고 하면 기존 a의 부모들은 포함되지 않는 문제가 발생.

추가로

int findParent(int node) {
	if (parentTable[node] == node)
		return parentTable[node];
	else
		return findParent(parentTable[node]);
}

(+) 재귀의 호출을 줄이는 방법

int findParent(int node) {
	if (parentTable[node] == node)
		return parentTable[node];
	else
		//return findParent(parentTable[node]);
        	return parentTable[node] = findParentTable[node];
}