[유니온-파인드] 무방향 그래프 속 사이클 찾기 / 예제 문제: 사이클 게임_백준

source: "이겻이 코딩테스트 이것이 취업을 위한 코딩 테스트다 with 파이썬" / 나동빈

유니온-파인드 연산을 통해 사이클 찾기

Union 연산은 그래프에서의 간선으로 표현될 수 있다. 즉 하나의 union 연산이 하나의 간선 연결과 같다. 따라서 간선을 하나씩 확인하면서 두 노드가 포함되어 있는 집합을 합치는 과정을 반복하는 것만으로도 그래프 내 '사이클'을 판별할 수 있다.

1. 각 간선을 확인하며 두 노드의 루트(parent) 노드를 확인한다.
   IF 서로의 parent가 다르면 두 노드에 대해 union 연산을 진행
   ELSE 서로 같다면 사이클이 발생한 것.
   
   
2. 그래프에 포함되어 있는 모든 간선에 대해 1번과정 반복

---

소스 코드

#include <bits/stdc++.h>
using namespace std;

int findParent(vector<int> &parentTable, int node) {
	if (parentTable[node] == node)
		return parentTable[node];
	else
		return parentTable[node] = findParent(parentTable, parentTable[node]);
}

bool solution(vector<vector<int>> arr, int n) {
	// 그래프 정보를 통해 사이클 확인
	
	// (1) parent table 생성하기
	vector<int> parentTabel(n + 1);
	for (int i = 1; i <= n; i++) {
		parentTabel[i] = i;
	}

	for (int i = 0; i < arr.size(); i++) {
		int nowNode = arr[i][0];
		int linkedNode = arr[i][1];
  		int nowNodeParent = findParent(parentTabel, nowNode);
 		int linkedNodeParent = findParent(parentTabel, linkedNode);
		if (nowNodeParent != linkedNodeParent) { // 부모가 다름.
			// Union
			if (nowNodeParent < linkedNodeParent)
				parentTabel[linkedNodeParent] = nowNodeParent;
			else
				parentTabel[nowNodeParent] = linkedNodeParent;
		}
		else {	// 부모가 같다? => 사이클 형성
			return true;
		}
	}

	// 끝까지 사이클이 없다면
	return false;
}

int main() {
	int n, e;	// n:노드 수 , e: 간선 수
	cin >> n >> e;

	vector<vector<int>> arr;
	for (int i = 0; i < e; i++) {
		int a, b;
		cin >> a >> b;
		
		arr.push_back(vector<int>({ a, b }));
	}

	for (int i = 0; i < arr.size(); i++) {
		cout << arr[i][0] << ", " << arr[i][1] << '\n';
	}


	bool result = solution(arr, n);
	if (result)
		cout << "사이클 존재" << '\n';
	else
		cout << "사이클 없음" << '\n';
}

---

예제 문제: 사이클 게임_백준

source: https://www.acmicpc.net/problem/20040

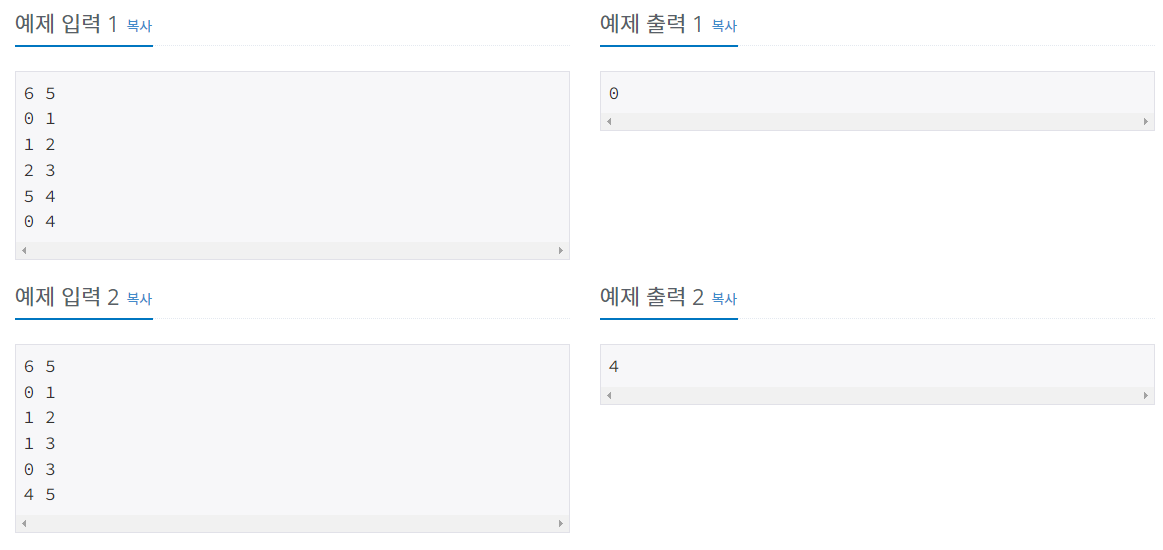
유니온-파인드 셋을 활용한 풀이

#include <iostream>
#include <vector>
using namespace std;

int N, M;
vector<pair<int, int>> Edges(1000000);

class UnionFindSet {
private:
	vector<int> parentTable;

public:
	UnionFindSet(int n) {
		parentTable.resize(n+1);
		for (int i = 1; i <= n; i++) {
			parentTable[i] = i;
		}
	}

	int Find(int node) {
		if (parentTable[node] == node)
			return node;
		else
			return parentTable[node] = Find(parentTable[node]);
	}

	void Union(int node1, int node2) {
		int node1Parent = Find(node1);
		int node2Parent = Find(node2);

		if (node1Parent < node2Parent) {
			parentTable[node2Parent] = node1Parent;
		}
		else
			parentTable[node1Parent] = node2Parent;
	}
};

bool checkCycle(UnionFindSet& uf, const pair<int, int>& edge) {
	int node1Parent = uf.Find(edge.first);
	int node2Parent = uf.Find(edge.second);

	if (node1Parent == node2Parent)
		return true;
	else
		return false;
}

int solution() {
	UnionFindSet uf(N);

	for (int idx = 0; idx < M; idx++) {
		pair<int, int> edge = Edges[idx];
		bool isCycle = checkCycle(uf, edge);

		if (isCycle)
			return idx + 1;

		uf.Union(edge.first, edge.second);
	}

	return 0;
}

int main() {
	cin >> N >> M;
	for (int i = 0; i < M; i++) {
		cin >> Edges[i].first >> Edges[i].second;
	}

	cout << solution() << endl;
	return 0;
}