[이진 탐색(Binary search)] 템플릿 코드와 예제 문제: 기타레슨_백준, 입국심사_프로그래머스

약 10,000,000(10M)개의 원소가 존재하는 배열이나 벡터에서 특정값을 검색하는 알고리즘은 순차탐색과 같은 O(n)의 시간복잡도 알고리즘으로 해결할 수 있으나 그 이상은 O(logn)의 시간복잡도를 가진 알고리즘을 해결해야 한다. 이때 이진탐색(binary search) 알고리즘이 필요하다.

---

템플릿 소스코드

#include <iostream>
#include <vector>
using namespace std;

int N, target;	// N: 원소의 갯수, target: 찾고자 하는 원소

int binarySearch(int target, vector<int>& vec, int start, int end) {
	while (start <= end) {
		// 중앙 인덱스
		int mid = (start + end) / 2;

		// target을 찾았다면 인덱스 반환 
		if (vec[mid] == target)
			return mid;

		// 중앙 인덱스에 있는 값보다 작으면 => 왼쪽 탐색
		else if (vec[mid] > target)
			end = mid - 1;
		// 중앙 인덱스에 있는 값보다 크다면 => 오른쪽 탐색
		else
			start = mid + 1;
	}

	// 끝까지 찾지 못하였다면 
	return -1;
}

int main() {
	cin >> N >> target;

	// 원소를 담을 벡터
	vector<int> vec(N);

	for (int i = 0; i < N; i++) {
		int x;
		cin >> vec[i];
	}

	// target이 존재하는 인덱스 출력
	int targetIdx = binarySearch(target, vec, 0, N - 1);
	if (targetIdx == -1)
		cout << "해당 원소가 존재하지 않음" << endl;
	else
		cout << "Idx: " << targetIdx << endl;

	return 0;
}

---

문제 1. 기타 레슨 (백준)

source: https://www.acmicpc.net/problem/2343

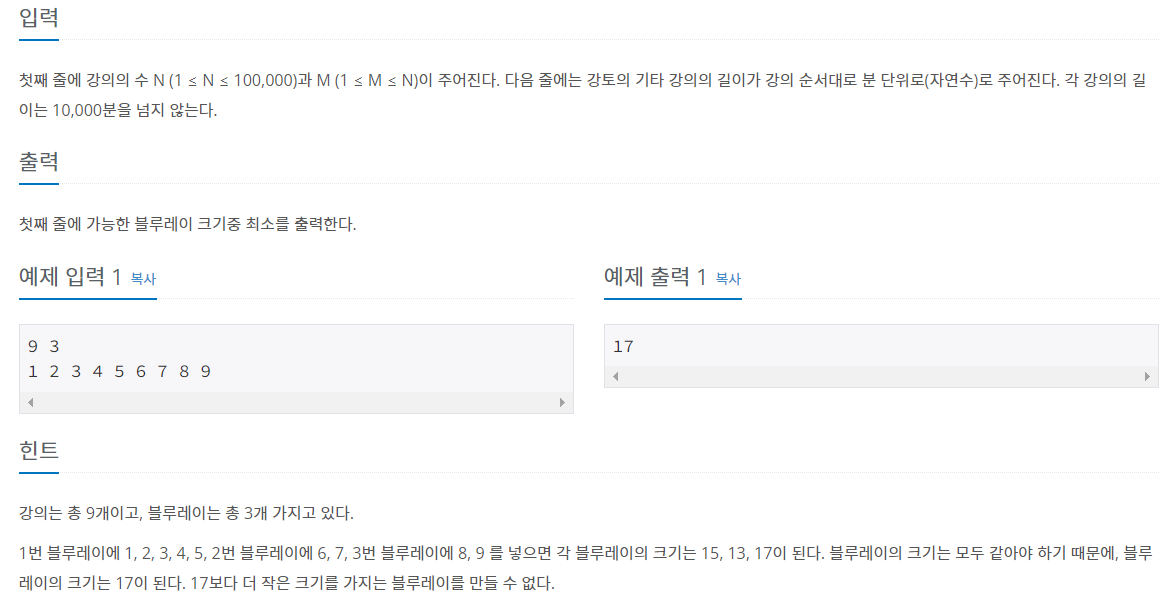
처음에 탐색의 기준을 못잡아서 애를 먹었던 문제..
가장 처음엔 이진.. 이진..에 뭔가 홀렸는지 문제를 풀면서 블루레이 숫자 M을 2^x개로 가정하며 풀게 되었다...

잘못된 풀이: 블루레이 수를 2^x개로 가정

// 블루레이 갯수가 2^x 일 때의 솔루션
int calcSum(vector<int>& vec, int start, int end) {
	int sum = 0;
	for (int i = start; i <= end; i++)
		sum += vec[i];

	return sum;
}

void DFS(vector<int>& videos, int start, int end, int divLevel, int& answer) {
	// 종료조건
	if (divLevel == M) {
		int sum = calcSum(videos, start, end);
		//cout << sum << endl;
		answer = max(answer, sum);
		return;
	}

	// 두 파트를 두 개로 쪼갤때 양 쪽의 원소들 합이 가장 균등하게 자른다.
	int mid = (start + end) / 2;
	// 왼쪽 합
	int leftSum = calcSum(videos, start, mid);
	// 오른쪽 합
	int rightSum = calcSum(videos, mid + 1, end);
	int minBalacne = abs(leftSum - rightSum);
	int minBalanceMid = mid;


	// 하나의 파트를 나눈다.
	int ss = start;	// 변동
	int ee = end;	// 변동
	while (ss <= ee) {
		mid = (ss + ee) / 2;

		leftSum = calcSum(videos, start, mid);
		rightSum = calcSum(videos, mid + 1, end);
		//int balance = leftSum - rightSum;

		// 딱 동일하게 나뉜다면,
		if (leftSum == rightSum) {
			DFS(videos, start, mid, divLevel*2, answer);
			DFS(videos, mid + 1, end, divLevel * 2, answer);
			return;
		}
		// 왼쪽sum에 수를 더 주는 경우
		else if (leftSum < rightSum) {
			// mid를 오른쪽으로 이동
			ss = mid + 1;
		}
		// 오른쪽 sum에 수를 더 주는 경우
		else {
			// mid를 완쪽으로 이동
			ee = mid - 1;
		}

		// 이동전 minBalance, minBalanceIdx 갱신
		if (minBalacne > abs(leftSum - rightSum)) {
			minBalacne = abs(leftSum - rightSum);
			minBalanceMid = mid;
		}
	}

	// 두 개로 쪼갠다.
	DFS(videos, start, minBalanceMid, divLevel*2, answer);
	DFS(videos, minBalanceMid + 1, end, divLevel * 2, answer);
	return;
}

// 강의 갯수: ~100,000
// 강의 길이: ~10,000
// 블루레이 크기: ~1,000,000,000
int solution() {
	// 0) videos 정렬
	// O(nlogn)
	auto endIter= videos.begin() + N;
	sort(videos.begin(), endIter);

	
	int answer = 0;
	DFS(videos, 0, N - 1, 1, answer);
	return answer;
}

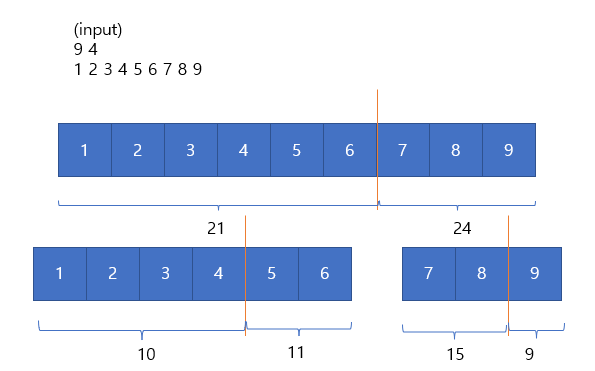
하나의 구간에서 왼쪽 합, 오른쪽 합이 가장 비슷한 구간으로 짜른다.
이를 M개의 구간으로 나눌 때까지 반복한다.

올바른 풀이

이진 탐색에서 중요한 것은 무엇을 탐색할 지 파악하는 것 같다. 블루레이의 길이를 탐색의 대상으로 두어 다시 풀었다.

• 초기 탐색의 범위: start: 0, end: 모든 비디오(강의) 길이의 합(최악: 1,000,000,000)
• mid = (start + end) / 2
• mid가 곧 하나의 블루레이 길이가 되며 판단한다.
  1) 하나의 블루레이 길이가 mid일 떄 모든 비디오를 담지 못한다면 mid를 늘린다.
  => start = mid + 1;
  2) 비디로을 모두 담는다면 mid를 줄여가며 블루레이 길이를 최대한 줄여본다.
  => end = mid - 1;
  => minBluelayLen = min(minBluelayLen, mid);

시간 복잡도: O(logK) * O(M)
( 0 <= k <= 1,000,000,000 )

int putVideos(int bluelayLen) {
	// 블루레이 하나당 bluelayLen만큼 담을 수 있다.
	
	int idx = 0;
	int putCnt = 0;
	// M개의 블루레이가 존재할 수 있다.
	for (int i = 0; i < M; i++) {
		int partSum = 0;
		for (; idx < N; idx++) {
			if (partSum + videos[idx] > bluelayLen) 
				// 해당 idx를 포함하면, 현재 부분이 정해준 bluelay 길이를 넘음
				break;
			

			putCnt++;
			partSum += videos[idx];
		}
	}

	return putCnt;
}

int solution() {
	int minBlueLayLen = 1e9;

	// 블루레이 길이를 탐색의 기준으로 잡는다.
	// end는 비디오 길이들의 합
	int start = 0;
	int end = 0;
	for (int i = 0; i < N; i++) {
		end += videos[i];
	}

	while (start <= end) {
		int mid = (start + end) / 2;
		
		// mid는 곧 블루레이의 길이라 볼 수 있다.
		int bluelayLen = mid;
		// bludelayLen과 M을 기반으로 비디오들을 담고, 담은 비디오 숫자를 리턴
		int putVideoNum = putVideos(bluelayLen);

		// 만약 비디오를 다 못 담았다면,,
		// => 블루레이 길이를 늘려야 함.
		// mid를 오른쪽으로..
		if (N > putVideoNum) {
			// 답이 될 수 없음
			start = mid + 1;
		}
		// 비디오를 모두 담았다면
		else {	// else if(N == putVideoNum)
			// 답이 될 수 있음 
			// 최소 블루레이 길이를 간직하고 mid를 왼쪽으로 더 이동해본다.
			minBlueLayLen = min(minBlueLayLen, bluelayLen);
			end = mid - 1;
		}
	}

	return minBlueLayLen;
}

=> 이진 탐색(하나의 블루레이 길이 탐색)과 mid를 통해 판단(putVideosNum을 통해 판단)하며 탐색의 범위를 좁힌다(start 또는 end 이동).
이러한 방식의 문제의 또 다른 예로는 아 문제를 참고하면 좋다.

reference: https://www.acmicpc.net/problem/2110

2022/06/17 복습

#include <iostream>
#include <vector>

using namespace std;

/*
블루레이의 적절한 길이를 '탐색'한다.
M개의 블루레이의 적절한 길이를 탐색하는 것이므로
적절한 길이에 대한 탐색이 진행되어야 한다. 
단순히 1부터 증가하는 방식으로는 시간초과가 발생한다.
따라서 O(logN)의 시간복잡도를 가진 탐색이 요구되고, 바로 이진탐색으로 진행해야 한다. 
*/

bool checkPossibleLen(int len, int numOfLectures, int numOfBluelays, const vector<int>& lectureTimes) {
	int cntBluelay = 1;
	int cntOneBlueLay = 0;
	for (int i = 0; i < numOfLectures; i++) {
		// 예외 처리, 하나의 블루레이에는 반드시 하나 이상의 영상을 담아야 한다.
		if (lectureTimes[i] > len)
			return false;

		cntOneBlueLay += lectureTimes[i];

		if (len < cntOneBlueLay) {
			cntBluelay++;
			cntOneBlueLay = lectureTimes[i];
		}
		else {
			// continue;
		}
	}

	if (cntBluelay > numOfBluelays)
		return false;
	else
		return true;
}

int solution(int numOfLectures, int numOfBluelays, const vector<int>& lectureTimes) {
	int answer = 0;

	// 적절한 블루레이 길이를 탐색한다.
	// 탐색의 범위
	// 0 ~ lectureTimesSum
	int lectureTimesSum = 0;
	for (int i = 0; i < numOfLectures; i++) {
		lectureTimesSum += lectureTimes[i];
	}

	int start = 0;
	int end = lectureTimesSum;
	while (start <= end) {						// O(logN)
		int mid = (start + end) / 2;

		// mid를 기준으로 탐색을 진행한다.
		// mid는 임시 블루레이 길이라 볼 수 있다. 
		
												// O(func) == total: O(logN) * O(func) 
		// if(m개의 블루레이 길이가 mid일 때 강의를 모두 담을 수 있는 경우)
			// 블루레이 길이를 더 줄여본다.
			// end = mid - 1;
		// else if(m개보다 적은 블루레이로 강의를 모두 담을 수 있는 경우)
			// 블루레이 길이를 더 줄여본다.
		if (checkPossibleLen(mid, numOfLectures, numOfBluelays, lectureTimes)) {
			end = mid - 1;
			answer = mid;
		}

		// else if(강의를 모두 못 담는 경우)
			// 블루레이 길이를 더 늘린다.
		else
			start = mid + 1;
	}

	return answer;
}

int main() {
	int numOfLectures;
	int numOfBluelays;
	cin >> numOfLectures >> numOfBluelays;

	vector<int> lectureTimes(numOfLectures);
	for (int i = 0; i < numOfLectures; i++) {
		cin >> lectureTimes[i];
	}

	int answer = solution(numOfLectures, numOfBluelays, lectureTimes);
	cout << answer << endl;

	return 0;
}

---

문제 2. 입국 심사 (프로그래머스)

source: https://programmers.co.kr/learn/courses/30/lessons/43238

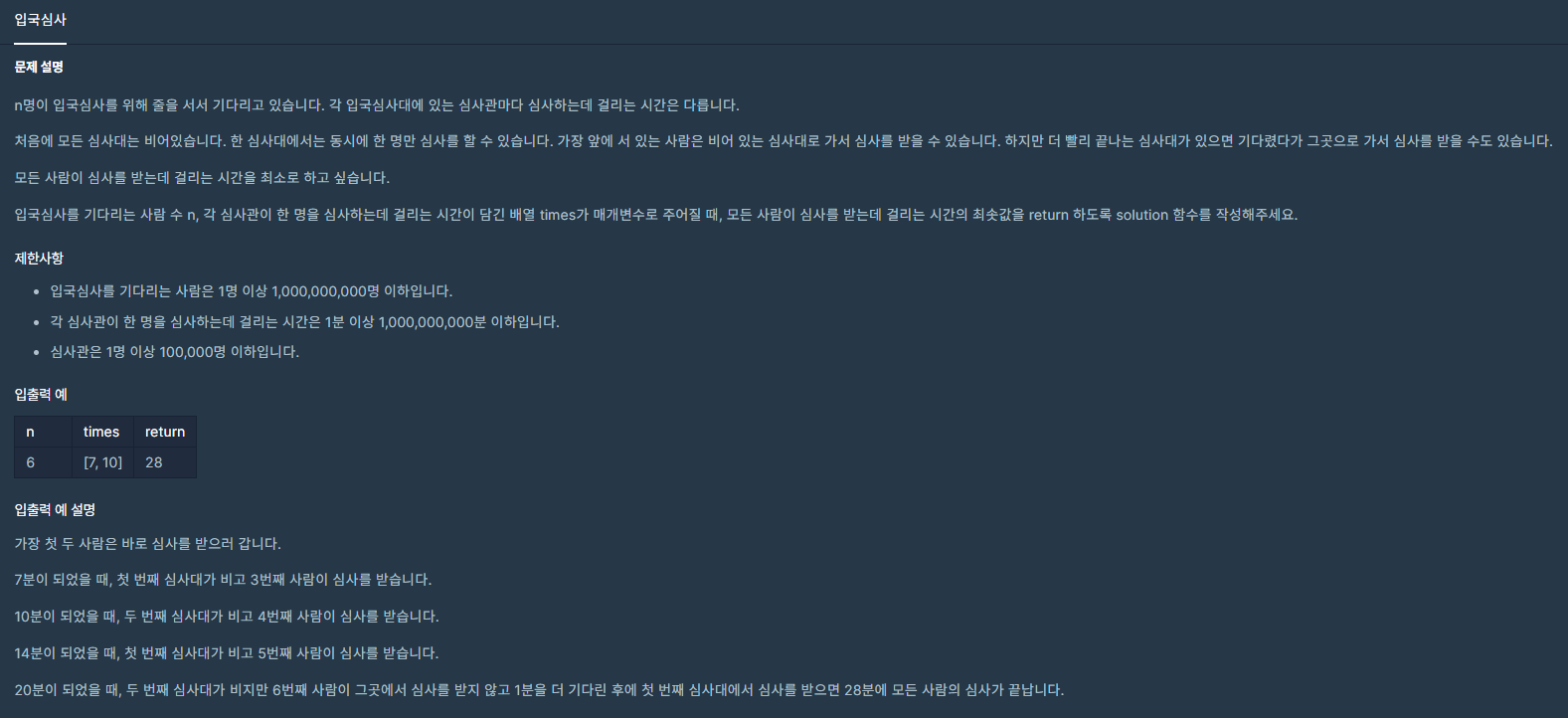
탐색의 대상을 '모든 사람이 심사를 받는데 걸리는 시간'으로 둔다.
start = 0 부터 end = 1e9*1e9 까지 이진 탐색으로 이 시간을 탐색한다.

• 만약 한 번의 턴에서 결정된 mid(시간)에서 모든 사람의 심사가 이루어 질 수 없다면(possible 함수로 판단) 시간을 증가시칸다.
  => start = mid + 1;
• 모든 사람의 심사가 이루어질 수 있다면 해당 시간을 저장하고, 시간을 감소 시킨다.
  => end = mid - 1;
  => minTime = min(minTime, mid);

시간 복잡도: O(logK) * O(심사관 수)
( 0 <= k <= 1e9x1e9 )

bool possible(long long n, vector<int>& times, long long mid){
    // 한직원이 맡을 수 있을 만큼 맡는다. 
    for(int i=0; i < times.size(); i++){
        int worker = i;
        // 직원이 한 고객을 대상으로 심사에 걸리는 시간
        int workerTime = times[worker];  
        
        // 직원이 mid 시간내에 맡을 수 있는 고객의 최대 수
        long long maxAssignment = mid / workerTime;
        
        n -= maxAssignment;
    }
    
    if(n > 0)
        // 모든 직원들이 최대로 심사를 하여도, 심사를 받지 못한 고객이 남아있음
        return false;  
    else
        return true;
}

long long solution(int n, vector<int> times) {
    long long answer = 1e9 * 1e9;
    
    // '모든 사람이 심사를 받는데 걸리는 시간'을 탐색의 대상으로 한다.
    // 적절한 start는 모르므로 그냥 1이라한다.
    // long long start = 1;
    // end는 가장 최악의 시나리오에서 걸리는 시간으로
    // long long end = 1e9 * 1e9;
    
    long long start = 1;
    long long end = 1e9 * 1e9;
    
    while(start <= end){
        long long mid = (start + end ) / 2;
        
        if(possible(n, times, mid)){
            // 최소의 시간을 저장
            answer = min(answer, mid);
            end = mid - 1;  // 시간을 줄여보기 ..
        }
        else {  // 시간을 늘려야 한다. => mid 증가
            start = mid + 1;
        }
        
    }
    
    return answer;
}