[DFS, DP] 재귀호출 시간복잡도 계산 & DFS+DP 풀이: (백준)2×n 타일링 2

깊이를 내려가면서 브랜치가 뻗어나가는 방식의 재귀호출 시간복잡도

source: https://www.youtube.com/watch?v=NyV0d5QadWM

=> 시간 복잡도: O(branch^depth)

ex) 재귀호출 방식의 피보나치 수열 시간복잡도

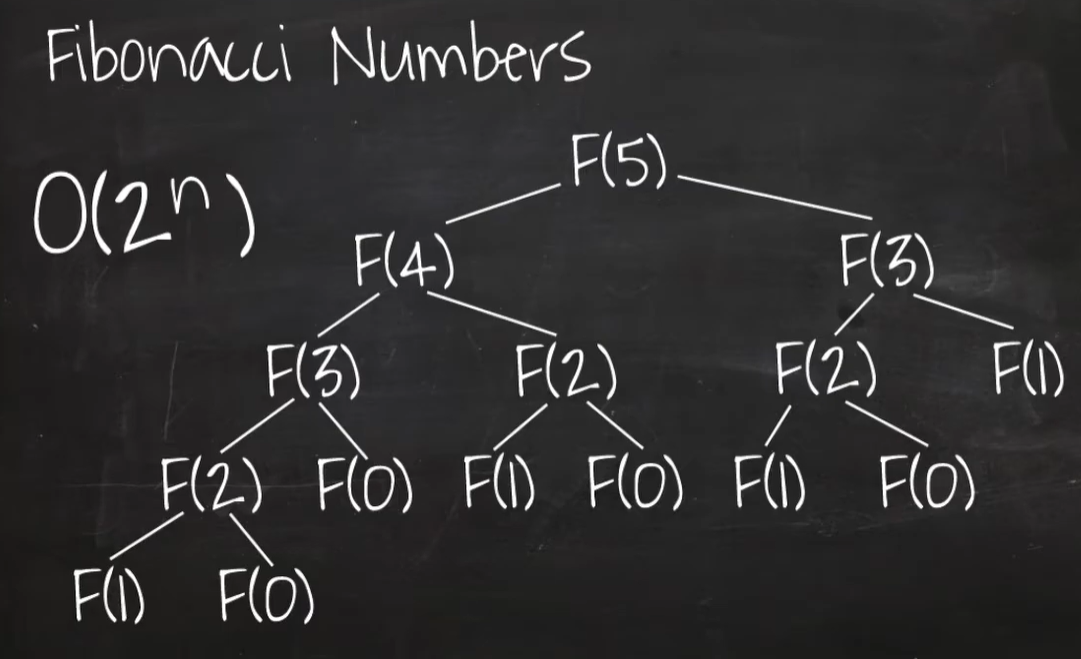
=> O(2^n)

source: https://www.youtube.com/watch?v=VcCkPrGaKrs&t=3s

---

(백준) 2×n 타일링 2

_

source: https://www.acmicpc.net/problem/11727

1) 단순 DFS(재귀) 풀이

#include <iostream>
#include <vector>
using namespace std;

const int MOD = 10007;

int N;

int DFS(int width) {
	// 종료조건
	if (width > N)
		return 0;
	else if (width == N)
		return 1;	// 한가지 방법 완성

	// 탐색
	int totalCnt = 0;

	// 3가지 방법 탐색
    // 1) 1x2 직사각형 
	if (width + 1 <= N) {
		totalCnt += DFS(width + 1);
	}
	// 2) 2x2 정사각형
	if (width + 2 <= N) {
		totalCnt += DFS(width + 2);
	}
	// 3) 2x1 직사각형 두개
	if (width + 2 <= N) {
		totalCnt += DFS(width + 2);
	}

	return totalCnt % MOD;
}

int solution() {
	// DFS 방식
	int answer = DFS(0) % MOD;

	return answer;
}

int main() {
	cin >> N;
	cout << solution() << endl;
}

==> 시간초과!
시간 복잡도: O(3^n)

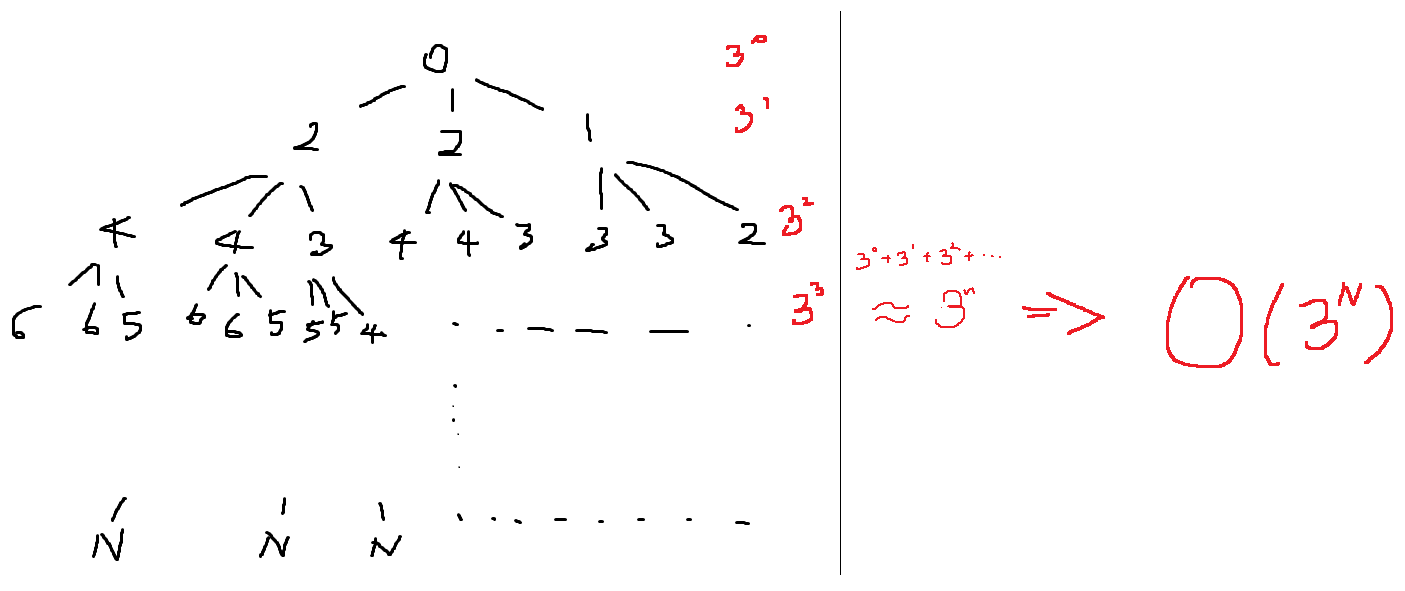
2) 메모제이션 활용

// 메모제이션 기법
int DP[1000 + 1];

int DFS(int width) {
	// 메모 활용
	if (DP[width])
		return DP[width];

	// 종료조건
	if (width > N)
		return 0;
	else if (width == N)
		return 1;	// 한가지 방법 완성

	// 탐색
	int totalCnt = 0;

	// 3가지 방법 탐색
	// 1) 1x2 직사각형 
	if (width + 1 <= N) {
		totalCnt += DFS(width + 1);
	}
	// 2) 2x2 정사각형
	if (width + 2 <= N) {
		totalCnt += DFS(width + 2);
	}
	// 3) 2x1 직사각형 두개
	if (width + 2 <= N) {
		totalCnt += DFS(width + 2);
	}

	// memozation
	DP[width] = totalCnt % MOD;
	return totalCnt % MOD;
}

=> 통과

+) Bottom-Up 방식

=> 시간 복잡도: O(n)

int BOTTOM_UP() {
	// 초기화
	DP[0] = 0;
	DP[1] = 1;
	DP[2] = 3;

	for (int i = 3; i <= N; i++) {
				// 1x2		// 2x2 사각형, 2*1 사각형(두개)
		DP[i] = (DP[i - 1] + DP[i - 2] * 2) % MOD;
	}


	return DP[N] % MOD;
}

int solution() {
	// DFS 방식(top-down 방식)
	//int answer = DFS(0) % MOD;

	// Bottom-up 방식
	int answer = BOTTOM_UP() % MOD;

	return answer;
}