룩업(Lookup, 조회)
- 룩업은 특정 원소가 컨테이너에 있는지 확인하거나 또는 컨테이너에서 특정 키(key)에 해당하는 값(value)을 찾는 작업을 의미함.
- 선형 자료구조인 경우 룩업 작업의 시간 복잡도는 O(N)
- 연관 컨테이너의 일종인 map 또는 set의 경우 룩업 작업의 시간 복잡도는 O(logN)
- 데이터가 어마무시하게 많다면 해시 테이블 자료구조를 사용한다.
해싱(Hashing)
- 정수형 데이터를 비롯하여, 데이터가 실수인 경우, 숫자가 아닌 경우, 범위가 자체가 큰 데이터인 경우 등 어떤 데이터 타입의 값이든 원하는 범위의 정수로 매핑하는 함수를 만들어 해시 테이블 구조를 활용할 수 있다. 이러한 매핑의 역할을 하는 것이 해시 함수이다.
- 해시 함수: 데이터 원소를 인자로 받고 정해진 범위의 정수를 반환
- 가장 간단한 해시 함수는 큰 범위의 정수를 인자로 받아 정해진 정수(n)로 나눈 나머지를 반환하는 모듈로 함수가 있겠다.
- 해시 값: 해시 함수에 의해 반환되는 숫자 값
- 서로 다른 데이터 원소에 대해 같은 해시 값을 반환할 수 있다. 즉, 다수의 키가 같은 값을 갖게 되는 현상이다. 이를 충돌(collision)이라 한다.
(1) 정수값을 저장하는 간단한 사전 예시 (같은 해시 값일 경우 덮어쓰기)
- 해시 테이블에 단순히 해당 키가 있는지만을 확인하는 작업임
- 키에 해당하는 값이 있는지를 확인하려면 아래 코드에 추가되는 구조가 있다.
#include <iostream>
#include <vector>
using namespace std;
using uint = unsigned int;
using namespace std;
// 해시_맵 클래스
class Hash_map {
private:
vector<int> data;
public:
// 해시 맵 생성자
Hash_map(size_t n) {
data = vector<int>(n, -1);
// 벡터의 모든 원소를 -1로 초기화
// data 벡터 값이 -1이라는 것은 해당 위치에 저장된 원소가 없음을 의미
}
// 삽입 함수
void insert(uint value) {
int n = data.size();
if (data[value % n] == -1) {
data[value % n] = value;
cout << value << "를 " << "[" << value % n << "] 위치에 삽입" << endl;
}
else {
cout << "기존에 저장된 " << data[value % n] << "를 덮어써 ";
data[value % n] = value;
cout << value << "를 " << "[" << value % n << "] 위치에 삽입" << endl;
}
}
// 룩업 함수
void find(uint value) {
int n = data.size();
if (data[value % n] == value) {
cout << "발견 !" << endl;
}
else {
cout << "없음 !" << endl;
}
}
// 삭제 함수
void erasse(uint value) {
int n = data.size();
if (data[value % n] == value) {
data[value % n] = -1;
cout << value << "를 삭제" << endl;
}
else {
cout << "해당 원소가 삽입된 적이 없거나 덮여써짐" << endl;
}
}
};
int main() {
Hash_map hashMap(7);
hashMap.insert(2);
hashMap.insert(25);
hashMap.insert(10);
hashMap.find(25);
hashMap.insert(100);
hashMap.find(100);
hashMap.find(2);
hashMap.erasse(25);
}
충돌 발생 시 해결법 1. 체이닝(chaining)
- 해시 테이블의 특정 위치에 하나의 데이터만을 저장하는 것이 아니라 하나의 연결 리스트를 저장한다.
- 달리 말하자면 특정 해시 값 위치에 하나의 원소만 저장되는 것이 아니라 여러 개의 리스트 형태로 저장
- 벡터 대신 연결 리스트를 사용하는 이유는 원소를 빠르게 삭제하기 위함
시간 복잡도
- 삽입: O(1)
- 룩업과 삭제: O(N) // N: 특정 위치에 존재하는 리스트의 길이
(2) 정수값을 저장하는 간단한 사전 예시 (같은 해시 값일 경우 덮어쓰기)
#include <iostream>
#include <vector>
/*체이닝 기법을 위해 추가*/
#include <list>
#include <algorithm>
using namespace std;
using uint = unsigned int;
using namespace std;
// 해시_맵_체이닝 클래스
class Hash_Chaining_map {
private:
vector<list<int>> data;
public:
// 해시 맵 생성자
Hash_Chaining_map(size_t n) {
data.resize(n);
}
// 삽입 함수
void insert(uint value) {
int n = data.size();
// 이미 값이 있는지 확인한 후 추가하도록 구현할수도 있음
data[value % n].push_back(value);
cout << value << "를 " << "[" << value % n << "] 위치에 삽입" << endl;
}
// 룩업 함수
void find(uint value) {
int n = data.size();
list<int>& chain = data[value % n];
// 룩업
for (auto iter = chain.begin(); iter != chain.end(); ++iter) {
if ((*iter) == value) {
cout << "발견!" << endl;
return;
}
}
cout << "없음!" << endl;
return;
}
// 삭제 함수
void erasse(uint value) {
int n = data.size();
list<int>& chain = data[value % n];
// 룩업
for (auto iter = chain.begin(); iter != chain.end();) {
if ((*iter) == value) {
iter = chain.erase(iter);
cout << value << "를 삭제" << endl;
}
else {
iter++;
}
}
}
};
int main() {
Hash_map hashMap(7);
/* 체이닝이 도입된 해시맵 */
{
Hash_Chaining_map hashMap(7);
hashMap.insert(2);
hashMap.insert(25);
hashMap.insert(10);
hashMap.insert(100);
hashMap.insert(55);
hashMap.find(100);
hashMap.find(2);
hashMap.erasse(2);
}
}
체이닝 기법의 Trade-off
- 해시 테이블이 저장할 키 개수에 비해 매우 작다면
=> 충돌이 많이 발생하게 되고, 리스트는 평균적으로 더 길어짐 - 너무 큰 해시 테이블을 가지고 있다면
=> 실제 데이터는 듬성듬성 존재하게 되므로 메모리 낭비가 발생
부하율(load factor)
- 부하율 = (전체 키 개수) / (해시 테이블 크기)
- 해시 테이블에서 각각의 리스트에 저장되는 키의 평균 개수를 나타낸다.
- 부하율 == 1
=> 매우 이상적인 상태로 모든 연산(룩업/삭제 포함)이 O(1)에 가깝게 작동하고 모든 메모리 공간을 적절하게 활용 - 부하율 < 1
=> 리스트당 키가 하나도 저장되지 않은 경우가 있음. 메모리 낭비로 이어짐 - 부하율 > 1
=> 리스트의 평균 길이가 1보다 크다는 의미. 룩업, 삭제 등의 함수 수행 시간 복잡도가 O(1)을 보장하지 못한다.
재해싱(rehashing)
- 해시 테이블의 부하율이 1 근방의 특정 값보다 너무 크거나 작아지면 해시 함수를 변경할 필요가 있음. 이를 재해싱이라 한다.
- 해시 함수를 수정하여 부하율이 1이 가까운 값이 되도록 만드는 것인데, 변경된 해시 함수에 의한 값의 분포와 부하율을 고려하여 해시 테이블의 크기도 변경할 수 있다.
부하율이 1이면 완벽한가?
- 부하율이 해시 테이블 성능을 결정하는 유일한 지표는 아님
- 크기가 7인 해시 테이블에 7개의 원소가 저장되어 있다고 가정했을 때 모든 원소가 같은 해시 값을 가져서 같은 버킷에 존재한다면 무의미하다.
- 룩업에 대한 시간 복잡도가 O(1)이 아닌 O(K)이다.
- 해시 함수가 서로 다른 키에 대해 가급적 겹치지 않고, 골고루 분포된 해시 값을 반환하여야 한다.
충돌 발생 시 해결법 2. 열린 주소 지정(open addressing)
- 체이닝처럼 해시 테이블에 추가적인 리스트를 붙여서 데이터를 저장하는 방식이 아닌 모든 원소를 해시 테이블 내부에 저장하는 방식
- 해시 테이블의 크기가 반드시 데이터 개수보다 커야 한다.
- 특정 해시 값에 해당하는 위치가 이미 사용되고 있다면 테이블의 다른 비어있는 위치를 탐색하는 것
- 다른 비어있는 위치를 탐색하는 방법은 여러 가지 있다.
- ex) 선형 탐색, 이차함수 탐색..
(1) 선형 탐색
- 가장 간단한 탐색 방법
- 특정 해시 값에서 충돌이 발생하면 해당 위치에서 하나씩 다음 셀(cell) 위치로 이동하면서 셀이 비어있는지 확인하고, 비어있는 셀을 찾으면 원소를 삽입
- hash(key)에 해당하는 셀이 이미 채워졌다면 hash(++key) 루프를 돌며 비어있는 셀을 탐색
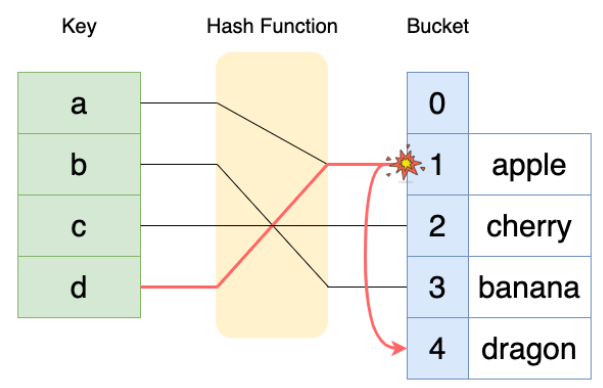
source: https://minho-jang.github.io/development/19/
선형 탐색의 클러스터(군집화) 문제
- 비슷한 해시 값 범위에 해당하는 키들이 반복적으로 많이 들어오면 해시 테이블의 특정 구간에 클러스터(군집) 형태로 값이 채워질 수 있다.
- 만약 원소 검색 시 해시 함수 반환 값(위치)가 큰 클러스터의 시작 위치를 가리킨다면 해당 클러스터의 맨 마지막 위치까지 선형 검색을 해야 할 수 있다. 즉, 검색 속도가 매우 느려질 수 있다.
(2) 이차함수 탐색
- 선형 탐색의 클러스터 문제를 극복하고자 생긴 탐색 방법
- 선형 탐색에서 hash(++key) 루프를 돌며 비어있는 셀을 탐색한 것과 달리 hash(key + (i++)^2) 루프를 돌며 탐색한다.
- hash(key) -> hash(key + 1) -> hash(key + 2) -> hash(key + 4) -> hash(key + 8) ..
- 이동 폭을 이차함수 형태로 증가시키면 데이터 군집이 나타날 활률이 상대적으로 줄어듬
