Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

32. 기하

조금 더 어려운 기하 문제를 풀어 봅시다.

Java / Python

8. 집으로

1069번

집으로 가는 문제

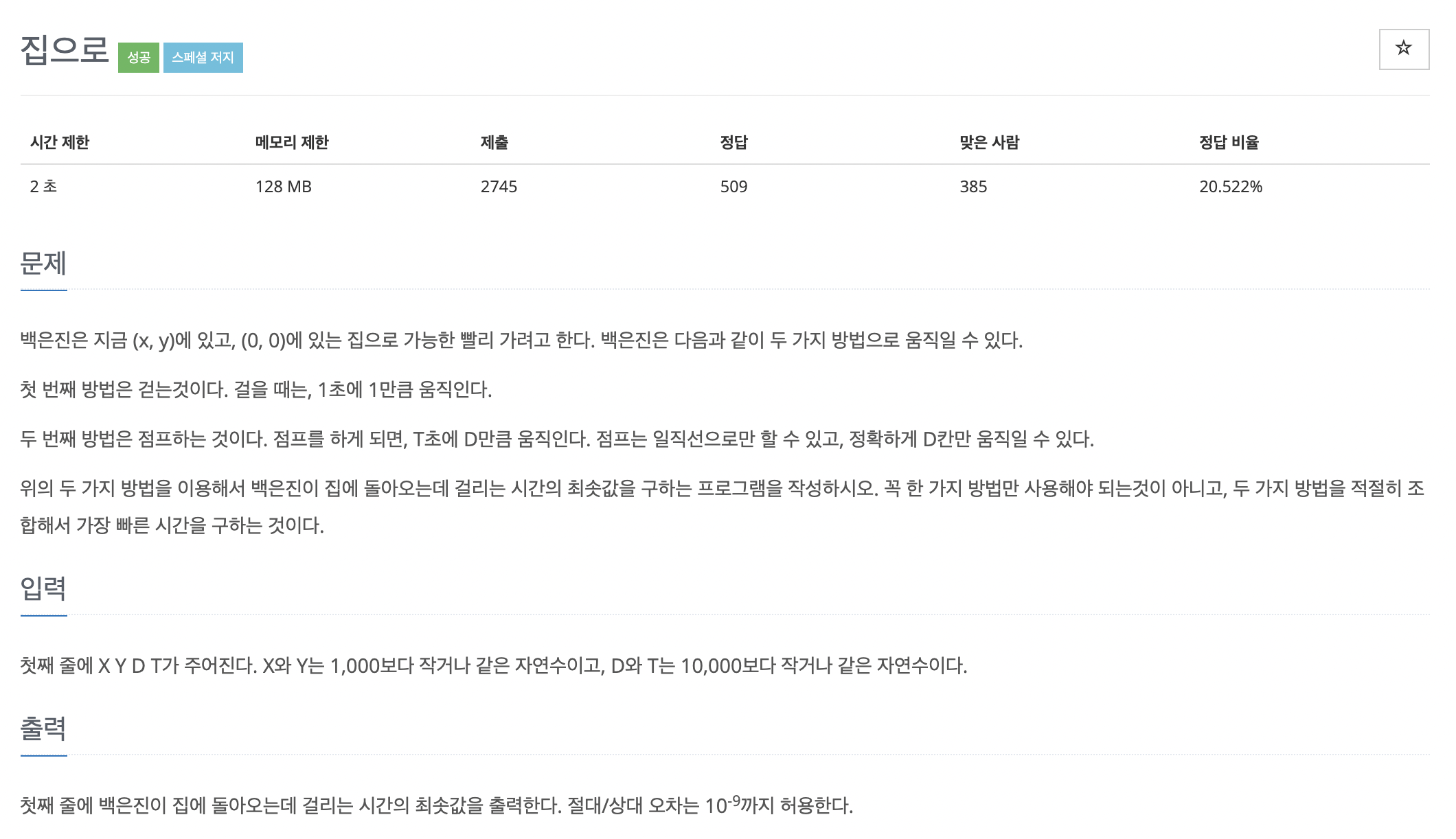
이번 문제는 집에 돌아오는데 걸리는 시간의 최솟값을 구하는 문제이다. 지금 (x, y)에 있고, (0, 0)에 있는 집으로 가능한 한 빨리 가려고 한다.

다음과 같이 두 가지 방법으로 움직일 수 있다. 첫 번째 방법은 걷는 것이고, 걸을 때는, 1초에 1만큼 움직인다.

두 번째 방법은 점프하는 것이다. 점프를 하게 되면, T 초에 D 만큼 움직인다. 점프는 일직선으로만 할 수 있고, 정확하게 D 칸만 움직일 수 있다.

점프하는 것보다 걷는 게 더 빠를 때는 바로 Dist 값을 출력한다.(sqrt(pow(X, 2) + pow(Y, 2)))

점프 횟수가 0일 경우, 걷기, 한번 점프 후 걷기, 2번 점프 중 작은 값을 고른다.

점프 횟수가 0이 아닐 경우, 점프 후 걷기와 한 번 더 점프 중 작은 값을 고른다.

• Java

import java.io.*;
import java.util.*;

public class Main {
	public static void main(String args[]) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		StringTokenizer st = new StringTokenizer(br.readLine());

		int x = Integer.parseInt(st.nextToken());
		int y = Integer.parseInt(st.nextToken());
		int d = Integer.parseInt(st.nextToken());
		int t = Integer.parseInt(st.nextToken());

		double dist = Math.sqrt(x * x + y * y);
		double result = dist;

		if (t > d) {
			bw.write(dist + "\n");
		} else {
			int jump = (int) (dist / d);

			double time = dist - d * jump;

			result = Math.min(result, time + t * jump);

			result = Math.min(result, d * (jump + 1) - dist + t * (jump + 1));

			if (jump > 0)
				result = Math.min(result, (double) (jump + 1) * t);
			else if (dist < d)
				result = Math.min(result, t * 2.0);

			bw.write(result + "\n");
		}
		bw.write(String.format("%.3f", result));

		bw.flush();
		bw.close();
		br.close();
	}
}

• Python

import sys
input = sys.stdin.readline

x,y,d,t = map(int,input().split())
dist = (x*x + y*y) ** 0.5
if t > d:
    print(dist)
else:
    n = dist // d
    print(min(t*n+dist-d*n,t*(n+1) if d<dist else min(dist,t+d-dist,2*t)))