Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

32. 기하

조금 더 어려운 기하 문제를 풀어 봅시다.

Java / Python

7. 두 원

7869번

삼각함수를 사용하는 문제

이번 문제는 두 원이 주어졌을 때, 교차하는 영역의 넓이를 소수점 셋째자리까지 구하는 문제이다.

삼각함수를 이용해 두 원의 교점을 구하는 식은 아래 블로그에서 공식을 잘 설명해주셔서 참고했다.
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=parkjy76&logNo=221454013299

간단히 정리하면 다음과 같다.

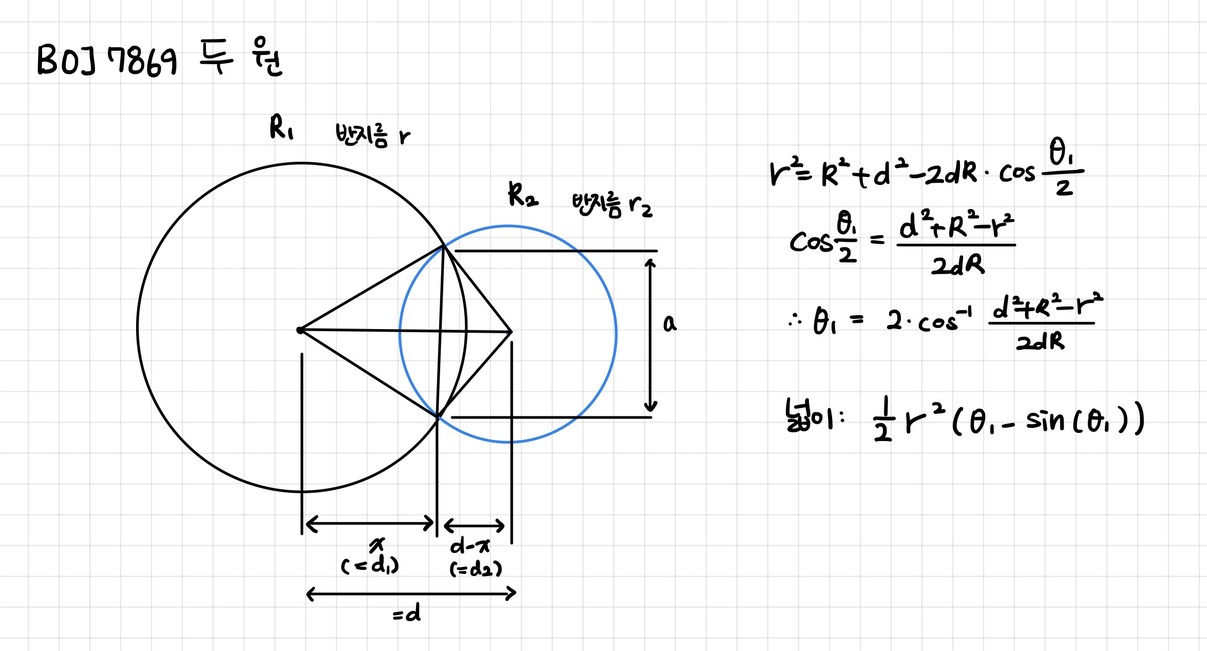
• Java

import java.io.*;
import java.util.*;

public class Main {
	public static void main(String args[]) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st = new StringTokenizer(br.readLine());

		double x1 = Double.parseDouble(st.nextToken());
		double y1 = Double.parseDouble(st.nextToken());
		double r1 = Double.parseDouble(st.nextToken());
		double x2 = Double.parseDouble(st.nextToken());
		double y2 = Double.parseDouble(st.nextToken());
		double r2 = Double.parseDouble(st.nextToken());

		double dist = getDistance(x1, y1, x2, y2);
		double result = 0;

		if (r1 + r2 <= dist)
			result = (double) 0;
		else if (Math.abs(r1 - r2) >= dist)
			result = Math.PI * Math.pow(Math.min(r1, r2), 2);
		else {
			double theta1 = Math.acos((r1 * r1 + dist * dist - r2 * r2) / (2 * r1 * dist));
			double theta2 = Math.acos((r2 * r2 + dist * dist - r1 * r1) / (2 * r2 * dist));

			double S1 = (r1 * r1 * theta1) - (r1 * r1 * Math.sin(2 * theta1) / 2);
			double S2 = (r2 * r2 * theta2) - (r2 * r2 * Math.sin(2 * theta2) / 2);
			result = S1 + S2;
		}
		bw.write(String.format("%.3f", result));

		bw.flush();
		bw.close();
		br.close();
	}

	public static double getDistance(double x1, double y1, double x2, double y2) {
		return Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));
	}
}

• Python

import math
import sys
input = sys.stdin.readline

x1, y1, r1, x2, y2, r2  = map(float, input().split())

def area(x1, y1, r1, x2, y2, r2):
    d = math.sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2))
    rr1 = r1 * r1
    rr2 = r2 * r2
    if (d > r2 + r1): # 원이 겹치지 않음
        return 0
    elif (d <= abs(r1 - r2) and r1 < r2): # 원1이 내부에
        return math.pi * rr1
    elif (d <= abs(r1 - r2) and r1 >= r2): # 원2이 내부에
        return math.pi * rr2
    else: # 두 점에서 만나는 경우
        phi = (math.acos((rr1 + (d * d) - rr2) / (2 * r1 * d))) * 2
        theta = (math.acos((rr2 + (d * d) - rr1) / (2 * r2 * d))) * 2
        area1 = 0.5 * rr2 * (theta - math.sin(theta))
        area2 = 0.5 * rr1 * (phi - math.sin(phi))
        return area1 + area2

result = float(round(1000 * area(x1, y1, r1, x2, y2, r2)) / 1000)
print('%.3f' % result)