Baekjoon Online Judge
algorithm practice
- 단계별 문제풀기
30. 최소 신장 트리
최소 비용으로 그래프의 모든 정점을 연결해 봅시다.
Java / Python
6. 다리 만들기 2
삼성 A형 기출 문제
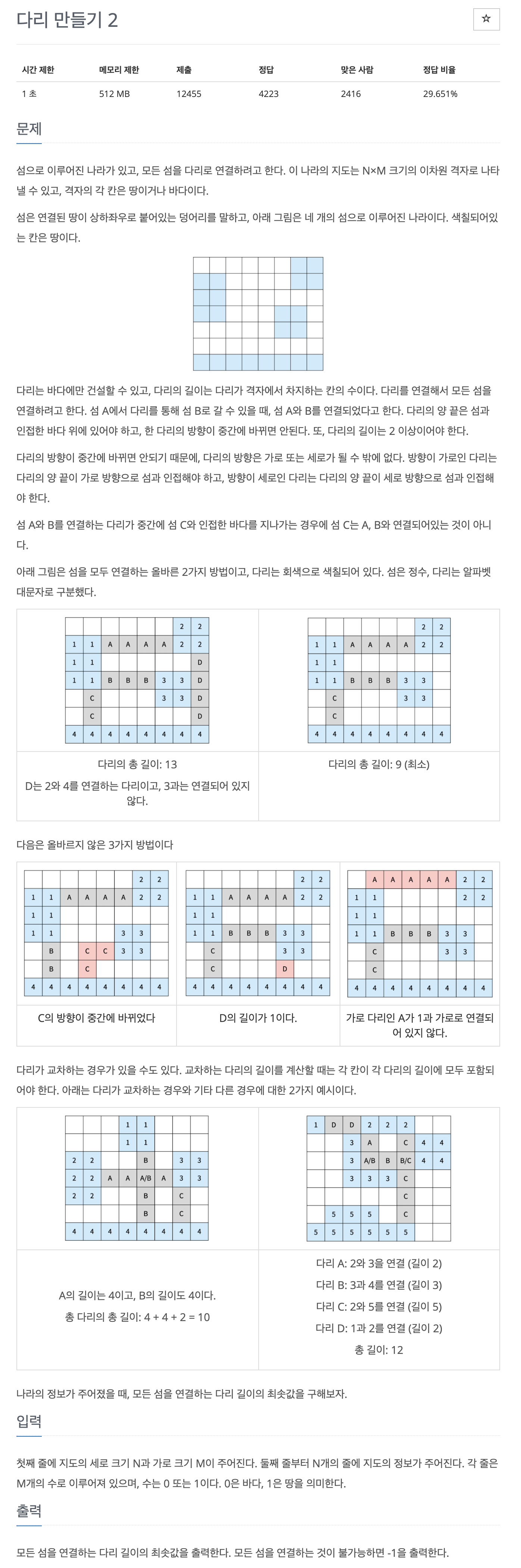
이번 문제는 나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구하는 문제이다.
- 각 섬을 구분하기 위해 섬마다 번호를 붙인다. (bfs활용)
- 각 좌표에서 최대로 만들 수 있는 다리를 모두 만들고, 우선 순위 큐에 넣는다. (크루스칼을 사용하기 위해 edge클래스를 만들어 Comparable를 implement해준다.)
- 크루스칼 알고리즘을 통해 최소 간선의 합을 구한다.
parent를 자기 자신으로 초기화하고, 부모를 찾는 함수 find와 합집합 연산을 해, 같은 부모를 가지도록 하는 union함수를 이용한다.
- Java
Point class : x 좌표, y 좌표 저장
Edge class : 간선의 정보를 저장, 연결된 노드 s, e와 비용 저장
import java.io.*;
import java.util.*;
public class Main {
static class Point {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
}
static class Edge implements Comparable<Edge> {
int s, e;
int cost;
Edge(int s, int e, int cost) {
this.s = s;
this.e = e;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
// Comparable을 통해 정렬 우선순위 (cost 기준)
return o.cost >= this.cost ? -1 : 1;
}
}
static int[] dx = { 0, 0, 1, -1 };
static int[] dy = { 1, -1, 0, 0 };
static int N, M;
static int[][] map;
static boolean[][] visit;
static PriorityQueue<Edge> pque = new PriorityQueue<Edge>();
static int[] parent;
static int island = 0;
static int bridge_cnt = 0;
static int result = 0;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
map = new int[N][M];
visit = new boolean[N][M];
// 입력 받기
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < M; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
// bfs 이용 - 섬 번호 부여
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (map[i][j] == 1 && !visit[i][j]) {
island++;
bfs(new Point(i, j));
}
}
}
// 다리 만들기
visit = new boolean[N][M];
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (map[i][j] != 0) {
makeBridge(new Point(i, j), map[i][j]);
}
}
}
// 크루스칼 알고리즘
parent = new int[island + 1];
for (int i = 0; i < parent.length; i++) {
parent[i] = i;
}
int size = pque.size();
for (int i = 0; i < size; i++) {
Edge tmp = pque.poll();
int a = find(tmp.s);
int b = find(tmp.e);
if (a == b)
continue;
union(tmp.s, tmp.e);
result += tmp.cost;
bridge_cnt++;
}
// result == 0 or 다리의 개수가 섬의 개수 - 1이 아닌 경우 -1 출력
if (result == 0 || bridge_cnt != island - 1) {
bw.write("-1\n");
} else {
bw.write(result + "\n");
}
bw.flush();
bw.close();
br.close();
}
// x의 부모 찾기
public static int find(int x) {
if (x == parent[x])
return x;
return parent[x] = find(parent[x]);
}
// y 부모를 x 부모로 치환하기 (x > y 일 경우 반대)
public static void union(int x, int y) {
x = find(x);
y = find(y);
if (x != y) {
parent[x] = y;
} else {
return;
}
}
public static void bfs(Point p) {
Queue<Point> q = new LinkedList<Point>();
visit[p.x][p.y] = true;
map[p.x][p.y] = island;
q.add(p);
while (!q.isEmpty()) {
Point temp = q.poll();
int x = temp.x;
int y = temp.y;
for (int i = 0; i < 4; i++) {
int x2 = x + dx[i];
int y2 = y + dy[i];
if (x2 >= 0 && x2 < N && y2 >= 0 && y2 < M && map[x2][y2] == 1 && !visit[x2][y2]) {
q.add(new Point(x2, y2));
map[x2][y2] = island;
visit[x2][y2] = true;
}
}
}
}
// 상하좌우 중 한 방향으로 계속 이동, 다른 섬이 나올 때까지 반복
public static void makeBridge(Point p, int num) {
int x2 = p.x;
int y2 = p.y;
int length = 0;
for (int i = 0; i < 4; i++) {
while (true) {
x2 = x2 + dx[i];
y2 = y2 + dy[i];
if (x2 >= 0 && x2 < N && y2 >= 0 && y2 < M) {
if (map[x2][y2] == num) {
// 자신과 같은 번호가 나오면
// 좌표와 length 초기화
length = 0;
x2 = p.x;
y2 = p.y;
break;
} else if (map[x2][y2] == 0) {
length++;
} else {
// 1보다 큰 경우 pque에 추가
if (length > 1) {
pque.add(new Edge(num, map[x2][y2], length));
}
length = 0;
x2 = p.x;
y2 = p.y;
break;
}
} else {
length = 0;
x2 = p.x;
y2 = p.y;
break;
}
}
}
}
}- Python
from collections import deque
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
N, M = map(int, input().split())
country = [list(map(int, input().split())) for _ in range(N)]
direction = [(-1, 0), (1, 0), (0, -1), (0, 1)]
queue = deque([]) # BFS에서 사용하는 큐(queue)
edge = [] # 생성 가능 다리 후보
cnt = 1 # 섬 고유번호
visit = [] # BFS 사용시 방문여부
for i in range(N):
for j in range(M):
if country[i][j] and (i, j) not in visit:
queue.append((i, j))
visit.append((i, j))
while queue:
r, c = queue.popleft()
country[r][c] = cnt
for idx in range(4):
nr = r + direction[idx][0]
nc = c + direction[idx][1]
if 0 <= nr < N and 0 <= nc < M:
if country[nr][nc] and (nr, nc) not in visit:
queue.append((nr, nc))
visit.append((nr, nc))
cnt += 1
# 생성 가능한 다리 찾기
def checkBridge(li):
start, cnt = 0, 0
flag = False
for idx in range(len(li)):
if li[idx] and not flag:
flag = True
start = li[idx]
elif not li[idx] and flag:
cnt += 1
elif li[idx] and flag and start != li[idx]:
if start and cnt >= 2:
if (start, li[idx], cnt) not in edge:
edge.append((start, li[idx], cnt))
cnt = 0
start = li[idx]
elif start == li[idx]:
cnt = 0
# 행
for row in country:
if sum(row):
checkBridge(row)
# 열
for col in list(zip(*country)):
if sum(col):
checkBridge(col)
edge = sorted(edge, key = lambda x:[x[2]])
parent = [i for i in range(cnt)]
rank = [1 for i in range(cnt)]
result = 0
# 크루스칼 알고리즘
def find(x):
if x == parent[x]:
return x
parent[x] = find(parent[x]) # 부모 테이블 갱신
return parent[x]
def union(x, y, w):
global result
x = find(x)
y = find(y)
if x == y: # 동일한 집합일 경우
return
result += w
if rank[x] < rank[y]:
rank[y] += rank[x]
parent[x] = y
else:
rank[x] += rank[y]
parent[y] = x
for e in edge:
union(e[0],e[1],e[2])
if max(rank) == cnt-1:
print(result)
else:
print(-1)최근 문제 중 가장 어려운 문제였던 것 같다..