Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

32. 기하

조금 더 어려운 기하 문제를 풀어 봅시다.

Java / Python

5. 선분 교차 3

20149번

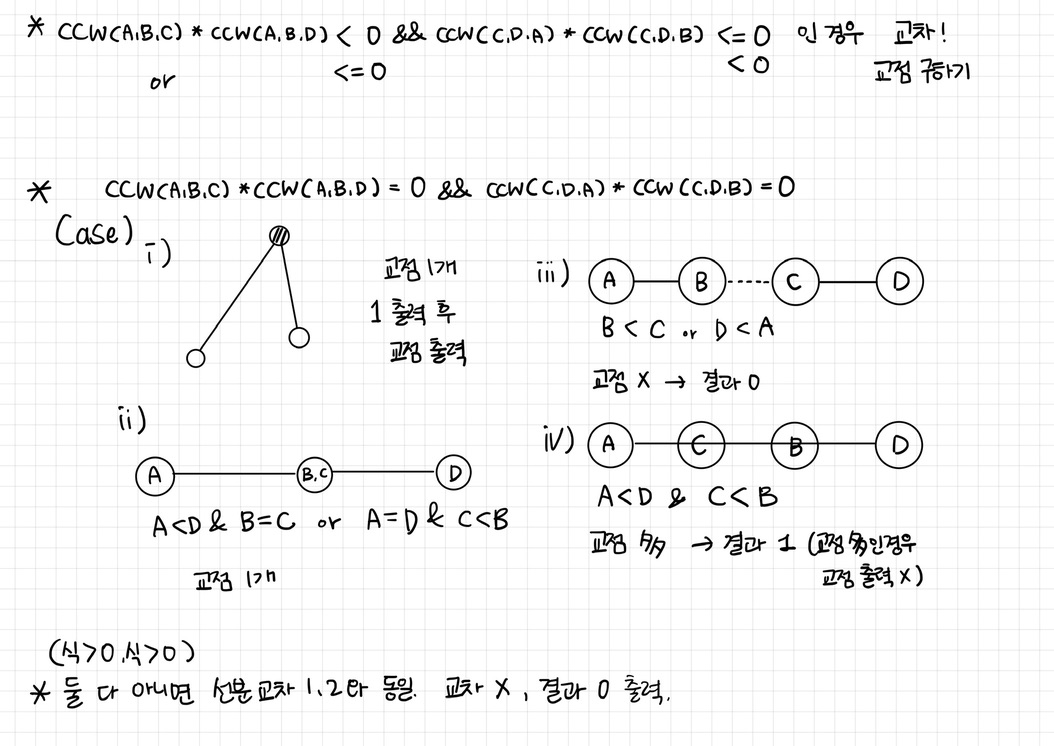
위와 같은데 교점의 좌표까지 찾는 문제

이번 문제는 2차원 좌표 평면 위의 두 선분 L1, L2가 주어졌을 때, 두 선분이 교차하는지 아닌지 구하는 문제이다. 한 선분의 끝 점이 다른 선분이나 끝 점 위에 있는 것도 교차하는 것으로 보면 된다. 저번 선분 교차 2 문제에서 교점의 좌표까지 찾아내는 문제이다. L1과 L2가 교차하면 첫째 줄에 1, 아니면 0을 출력하고,
두 선분이 한 점에서 교차하는 경우 둘째 줄에 교차하는 점의 x좌표와 y좌표를 공백으로 구분해 출력한다. 한 점에서 교차하지 않는 경우에는 둘째 줄을 출력하지 않는다.

CCW를 이용하는 문제이다.

• Java

import java.io.*;
import java.util.*;

public class Main {
	static class Point {
		int x, y;

		public Point(int x, int y) {
			this.x = x;
			this.y = y;
		}
	}

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st;
		StringBuilder sb = new StringBuilder();

		Point[] point = new Point[4];

		int x1, y1, x2, y2, x3, y3, x4, y4;

		st = new StringTokenizer(br.readLine());
		x1 = Integer.parseInt(st.nextToken());
		y1 = Integer.parseInt(st.nextToken());
		x2 = Integer.parseInt(st.nextToken());
		y2 = Integer.parseInt(st.nextToken());

		st = new StringTokenizer(br.readLine());
		x3 = Integer.parseInt(st.nextToken());
		y3 = Integer.parseInt(st.nextToken());
		x4 = Integer.parseInt(st.nextToken());
		y4 = Integer.parseInt(st.nextToken());

		point[0] = new Point(x1, y1);
		point[1] = new Point(x2, y2);
		point[2] = new Point(x3, y3);
		point[3] = new Point(x4, y4);

		bw.write(solve(point) + "\n");

		bw.flush();
		bw.close();
		br.close();
	}

	public static String solve(Point[] p) {
		StringBuilder sb = new StringBuilder();

		int p123 = ccw(p[0], p[1], p[2]);
		int p124 = ccw(p[0], p[1], p[3]);
		int p341 = ccw(p[2], p[3], p[0]);
		int p342 = ccw(p[2], p[3], p[1]);
		int S12 = p123 * p124;
		int S34 = p341 * p342;

		if (S12 <= 0 && S34 < 0 || S12 < 0 && S34 <= 0) {
			sb.append(1).append('\n');
			String T1 = getSlope(p[0], p[1]), T2 = getSlope(p[2], p[3]);
			double x, y;
			if (T1.equals("INF")) {
				x = p[0].x;
				double sl2 = Double.parseDouble(T2);
				y = sl2 * (x - p[2].x) + p[2].y;
			} else if (T2.equals("INF")) {
				x = p[2].x;
				double sl1 = Double.parseDouble(T1);
				y = sl1 * (x - p[0].x) + p[0].y;
			} else {
				double sl1 = Double.parseDouble(T1), sl2 = Double.parseDouble(T2);
				x = (sl1 * p[0].x - sl2 * p[2].x + p[2].y - p[0].y) / (sl1 - sl2);
				y = sl1 * (x - p[0].x) + p[0].y;
			}
			sb.append(x).append(' ').append(y);
		} else if (S12 == 0 && S34 == 0) {
			if (p123 == 0 && p124 == 0 && p341 == 0 && p342 == 0) {
				int n = isCrossed(p);
				if (n > 0)
					sb.append(1);
				else
					sb.append(0);

				if (n == 2) {
					sb.append('\n');
					if (p[0].x == p[2].x && p[0].y == p[2].y || p[0].x == p[3].x && p[0].y == p[3].y)
						sb.append(p[0].x).append(' ').append(p[0].y);
					else if (p[1].x == p[2].x && p[1].y == p[2].y || p[1].x == p[3].x && p[1].y == p[3].y)
						sb.append(p[1].x).append(' ').append(p[1].y);
				}
			} else {
				sb.append(1).append('\n');
				if (p[0].x == p[2].x && p[0].y == p[2].y || p[0].x == p[3].x && p[0].y == p[3].y)
					sb.append(p[0].x).append(' ').append(p[0].y);
				else if (p[1].x == p[2].x && p[1].y == p[2].y || p[1].x == p[3].x && p[1].y == p[3].y)
					sb.append(p[1].x).append(' ').append(p[1].y);
			}
		} else
			sb.append(0);

		return sb.toString();
	}

	public static int ccw(Point p1, Point p2, Point p3) {
		// CCW 공식 (x1y2+x2y3+x3y1)−(y1x2+y2x3+y3x1)
		long result = ((long)p1.x * p2.y + (long)p2.x * p3.y + (long)p3.x * p1.y) - ((long)p1.y * p2.x + (long)p2.y * p3.x + (long)p3.y * p1.x);
		if (result == 0) // 일직선
			return 0;
		return result > 0 ? 1 : -1;
	}

	private static String getSlope(Point p1, Point p2) {
		if (p1.x == p2.x)
			return "INF";
		double s = ((double) p2.y - p1.y) / (p2.x - p1.x);
		return String.valueOf(s);
	}

	public static int isCrossed(Point[] p) {
		int A, B, C, D;
		if (p[0].x == p[1].x) {
			A = Math.min(p[0].y, p[1].y);
			B = Math.max(p[0].y, p[1].y);
			C = Math.min(p[2].y, p[3].y);
			D = Math.max(p[2].y, p[3].y);
		} else {
			A = Math.min(p[0].x, p[1].x);
			B = Math.max(p[0].x, p[1].x);
			C = Math.min(p[2].x, p[3].x);
			D = Math.max(p[2].x, p[3].x);
		}

		if (A == D || B == C)
			return 2;
		else if (A < D && C < B)
			return 1;
		else
			return 0;
	}
}

• Python

import sys
input = sys.stdin.readline
point = []
x1, y1, x2, y2 = map(int, input().split())
x3, y3, x4, y4 = map(int, input().split())

point.append([x1, y1])
point.append([x2, y2])
point.append([x3, y3])
point.append([x4, y4])

def check(a, b, c, d):
    if ccw(a, b, c) * ccw(a, b, d) == 0:
        if ccw(c, d, a) * ccw(c, d, b) == 0:
            if a > b:
                a, b = b, a
            if c > d:
                c, d = d, c
            if b >= c and a <= d:
                return True
            else:
                return False
    if ccw(a, b, c) * ccw(a, b, d) <= 0:
        if ccw(c, d, a) * ccw(c, d, b) <= 0:
            return True
    return False

def ccw(p1, p2, p3):
    return (p2[0]-p1[0])*(p3[1]-p1[1]) - (p3[0]-p1[0])*(p2[1]-p1[1])

if check(point[0], point[1], point[2], point[3]):
    print(1)
    try:
        x = ((x1*y2-y1*x2)*(x3-x4)-(x1-x2)*(x3*y4-y3*x4))/((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4))
        y = ((x1*y2-y1*x2)*(y3-y4)-(y1-y2)*(x3*y4-y3*x4))/((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4))
        print(x, y)
    except:
        if point[0] > point[1]:
            point[0], point[1] = point[1], point[0]
        if point[2] > point[3]:
            point[2], point[3] = point[3], point[2]
        if point[1] == point[2]:
            print(point[1][0], point[1][1])
        elif point[0] == point[3]:
            print(point[0][0], point[0][1])
else:
    print(0)

해당 코드를 설명을 잘 해주셔서 아래 블로그를 통해 공부했습니다!
감사합니다!
참고 블로그