Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

32. 기하

조금 더 어려운 기하 문제를 풀어 봅시다.

Java / Python

6. 선분 그룹

2162번

선분 교차를 응용하는 문제

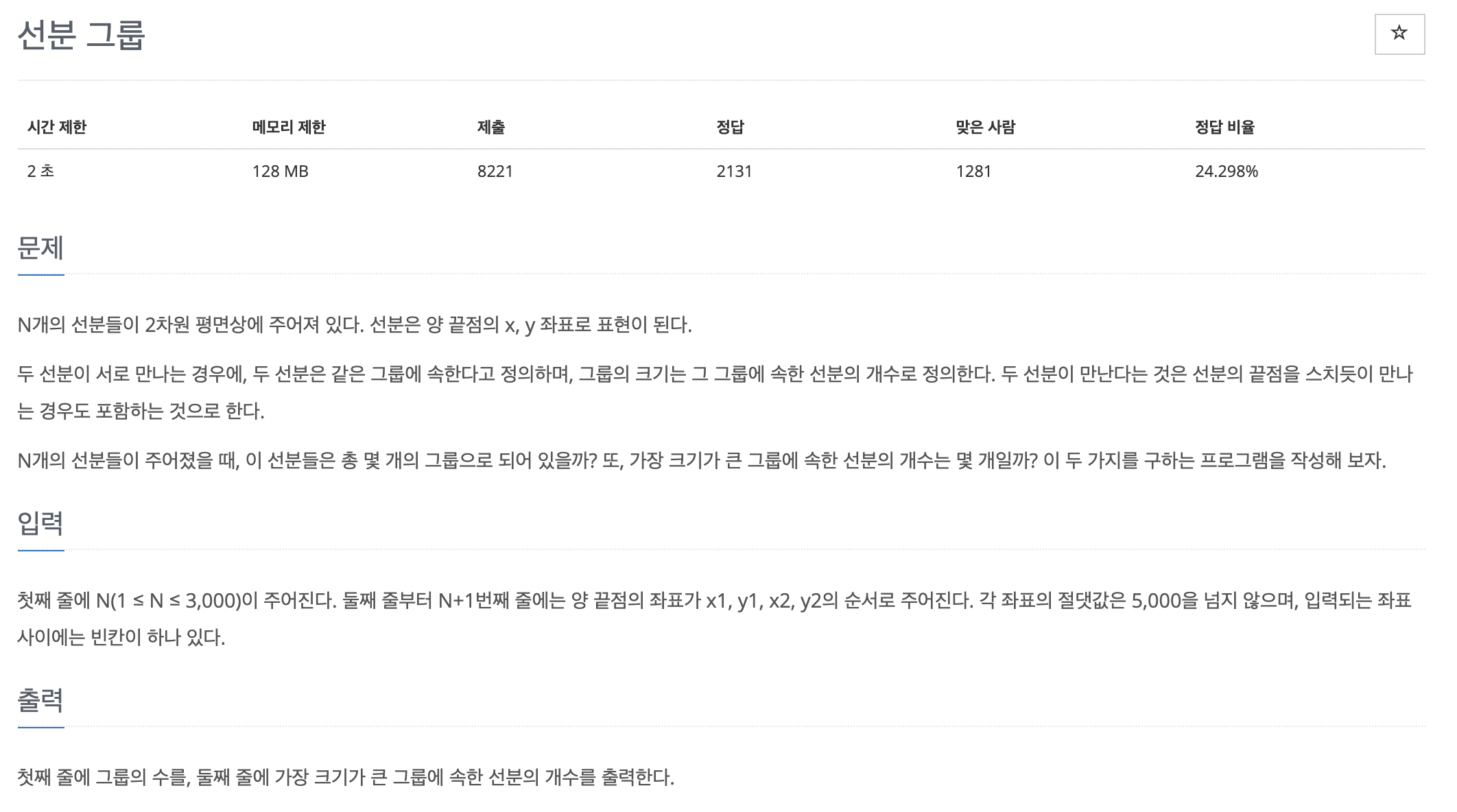
이번 문제는 N개의 선분들이 주어졌을 때, 이 선분들은 총 몇 개의 그룹으로 되어 있는지, 가장 크기가 큰 그룹에 속한 선분의 개수는 몇 개인지, 이 두 가지를 구하는 문제이다.

CCW와 크루스칼 알고리즘을 풀 때 사용해봤던, union, find 함수와 Parent를 이용한다.

• Java

import java.io.*;
import java.util.*;

public class Main {
	static class Line {
		long x1, y1, x2, y2;

		public Line(long x1, long y1, long x2, long y2) {
			this.x1 = x1;
			this.y1 = y1;
			this.x2 = x2;
			this.y2 = y2;
		}
	}

	static int[] parent;

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st;

		int N = Integer.parseInt(br.readLine());
		Line[] l = new Line[N + 1];
		parent = new int[N + 1];

		for (int i = 1; i <= N; i++) {
			parent[i] = i;
		}

		long x1, y1, x2, y2;

		for (int i = 1; i <= N; i++) {
			st = new StringTokenizer(br.readLine());

			x1 = Long.parseLong(st.nextToken());
			y1 = Long.parseLong(st.nextToken());
			x2 = Long.parseLong(st.nextToken());
			y2 = Long.parseLong(st.nextToken());

			l[i] = new Line(x1, y1, x2, y2);
		}
		int l_parent, r_parent;
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= N; j++) {
				if (i == j)
					continue;
				l_parent = find(i);
				r_parent = find(j);

				if (l_parent != r_parent) {
					if (isCrossed(l[i], l[j])) {
						union(i, j);
					}
				}
			}
		}
		int[] cnt = new int[N + 1];
		int max = 0;
		int size = 0;

		for (int i = 1; i <= N; i++) {
			cnt[parent[i]]++;
		}

		for (int i = 1; i <= N; i++) {
			if (max < cnt[i])
				max = cnt[i];
			if (cnt[i] != 0) {
				size++;
			}
		}

		bw.write(size + "\n" + max + "\n");

		bw.flush();
		bw.close();
		br.close();
	}

	public static int ccw(long x1, long y1, long x2, long y2, long x3, long y3) {
		// CCW 공식 (x1y2+x2y3+x3y1)−(y1x2+y2x3+y3x1)
		long result = (x1 * y2 + x2 * y3 + x3 * y1) - (y1 * x2 + y2 * x3 + y3 * x1);
		if (result == 0) // 일직선
			return 0;
		return result > 0 ? 1 : -1;
	}

	// x의 부모 찾기
	public static int find(int x) {
		if (x == parent[x])
			return x;

		return parent[x] = find(parent[x]);
	}

	// y 부모를 x 부모로 치환하기 (x > y 일 경우 반대)
	public static void union(int x, int y) {
		x = find(x);
		y = find(y);

		if (x != y) {
			parent[x] = y;
		} else {
			return;
		}
	}

	public static boolean isCrossed(Line l1, Line l2) {
		long check1 = ccw(l1.x1, l1.y1, l1.x2, l1.y2, l2.x1, l2.y1) * ccw(l1.x1, l1.y1, l1.x2, l1.y2, l2.x2, l2.y2);

		long check2 = ccw(l2.x1, l2.y1, l2.x2, l2.y2, l1.x1, l1.y1) * ccw(l2.x1, l2.y1, l2.x2, l2.y2, l1.x2, l1.y2);

		if (check1 == 0 && check2 == 0) {
			return isOverlapped(l1, l2);
		}
		return check1 <= 0 && check2 <= 0;
	}

	public static boolean isOverlapped(Line l1, Line l2) {
		if (Math.max(l1.x1, l1.x2) < Math.min(l2.x1, l2.x2))
			return false;
		if (Math.max(l2.x1, l2.x2) < Math.min(l1.x1, l1.x2))
			return false;
		if (Math.max(l1.y1, l1.y2) < Math.min(l2.y1, l2.y2))
			return false;
		if (Math.max(l2.y1, l2.y2) < Math.min(l1.y1, l1.y2))
			return false;
		return true;
	}
}

• Python (-시간 초과 / Pypy3)

import sys
input = sys.stdin.readline
N = int(input())
lines = [[]] + [list(map(int, input().split())) for _ in range(N)]
parent = [-1 for _ in range(N + 1)]

def ccw(x1, y1, x2, y2, x3, y3):
    result = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)

    if result > 0:
        return 1
    elif result == 0:
        return 0
    else:
        return -1

def check(x1, y1, x2, y2, x3, y3, x4, y4):
    if ccw(x1, y1, x2, y2, x3, y3) * ccw(x1, y1, x2, y2, x4, y4) == 0 and ccw(x3, y3, x4, y4, x1, y1) * ccw(x3, y3, x4, y4, x2, y2) == 0:
        if min(x1, x2) <= max(x3, x4) and min(x3, x4) <= max(x1, x2) and min(y1, y2) <= max(y3, y4) and min(y3, y4) <= max(y1, y2):
            return 1
    elif ccw(x1, y1, x2, y2, x3, y3) * ccw(x1, y1, x2, y2, x4, y4) <= 0 and ccw(x3, y3, x4, y4, x1, y1) * ccw(x3, y3, x4, y4, x2, y2) <= 0:
        return 1 
    return 0

# 크루스칼 알고리즘
def find(x):
    if parent[x] < 0:
        return x
    parent[x] = find(parent[x]) # 부모 테이블 갱신
    return parent[x]


def union(x, y):
    x = find(x) 
    y = find(y)

    if x == y:
        return
    
    if parent[x] < parent[y]:
        parent[x] += parent[y]
        parent[y] = x
    else:
        parent[y] += parent[x]
        parent[x] = y

for i in range(1, N):
    for j in range(i + 1, N + 1):
        x1, y1, x2, y2 = lines[i]
        x3, y3, x4, y4 = lines[j]
        if check(x1, y1, x2, y2, x3, y3, x4, y4):
            union(i, j)

cnt = 0
max_value = 0

for i in parent[1:]:
    if i < 0:
        cnt += 1
        max_value = max(max_value, abs(i))

print(cnt)
print(max_value)