Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

31. 트리에서의 동적 계획법

트리에 동적 계획법을 적용해 봅시다.

Java / Python

2. 트리의 독립집합

2213번

트리의 최대 독립 집합을 구하는 문제. 일반적인 그래프에서 최대 독립 집합을 구하는 문제는 NP-하드로, 효율적인 알고리즘이 알려지지 않았습니다.

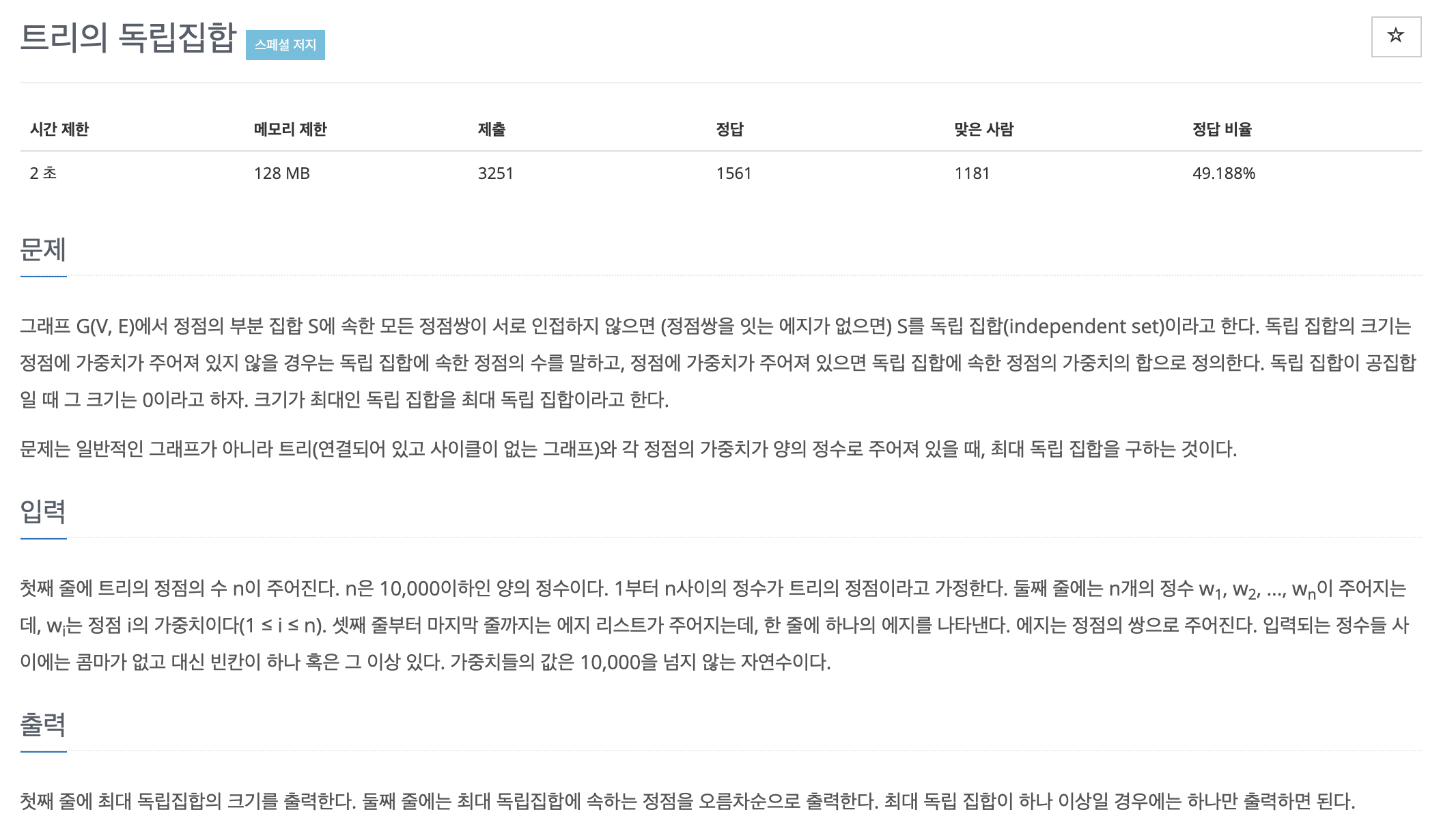
이번 문제는 일반적인 그래프가 아니라 트리(연결되어 있고 사이클이 없는 그래프)와 각 정점의 가중치가 양의 정수로 주어져 있을 때, 최대 독립 집합을 구하는 문제이다.

트리에서 DP를 사용하는 문제이다.

• Java

import java.util.*;
import java.io.*;

public class Main {
	static int N;
	static int[] dp, arr, select;
	static ArrayList<ArrayList<Integer>> list = new ArrayList<>();
	static ArrayList<ArrayList<Integer>> tree = new ArrayList<>();
	static PriorityQueue<Integer> pque = new PriorityQueue<>();

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringBuilder sb = new StringBuilder();

		N = Integer.parseInt(br.readLine());

		arr = new int[N + 1];
		dp = new int[N + 1];
		select = new int[N + 1];

		for (int i = 0; i <= N; i++) {
			list.add(new ArrayList<>());
			tree.add(new ArrayList<>());
		}

		StringTokenizer st = new StringTokenizer(br.readLine());

		for (int i = 1; i <= N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}

		for (int i = 0; i < N - 1; i++) {
			st = new StringTokenizer(br.readLine());
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());
			list.get(a).add(b);
			list.get(b).add(a);
		}

		buildTree(1, -1);

		int t1 = dp(1, 0);
		int t2 = dp(1, 1);

		if (t1 > t2) {
			select[1] = 0;
		} else {
			select[1] = 1;
		}
		sb.append(String.valueOf(Math.max(t1, t2))).append("\n");

		findNode(1, select[1]);

		while (!pque.isEmpty()) {
			sb.append(pque.poll()).append(" ");
		}

		bw.write(sb.toString());
		bw.flush();
		bw.close();
		br.close();
	}

	static int dp(int now, int node) {
		int result = 0;

		if (node == 1) {
			for (int next : tree.get(now)) {
				result += dp(next, 0);

			}
			return result + arr[now];
		} else {
			for (int next : tree.get(now)) {
				int t1 = dp(next, 0);
				int t2 = dp(next, 1);

				if (t1 > t2) {
					select[next] = 0;
				} else {
					select[next] = 1;
				}
				result += Math.max(t1, t2);
			}
			return result;
		}
	}

	static void buildTree(int now, int p) {
		for (int child : list.get(now)) {
			if (child != p) {
				tree.get(now).add(child);
				buildTree(child, now);
			}
		}
	}

	static void findNode(int now, int node) {
		if (node == 0) {
			for (int next : tree.get(now)) {
				findNode(next, select[next]);
			}
		} else if (node == 1) {
			pque.offer(now);
			for (int next : tree.get(now)) {
				findNode(next, 0);
			}
		}
	}
}

• Python

각 정점에 대하여 자신을 포함했을때의 최댓값과 포함하지 않았을때의 최댓값을 동적 프로그래밍으로 구하는 방식이다. dp[1][0]은 자기 자신을 포함했을때의 최댓값, dp[1][1]이라면 포함하지 않았을때의 최댓값이며 (최댓값을 구했을때의 정점번호도 저장) DFS를 이용해 가장 깊은곳부터 값을 더해나간다.

import sys
input = sys.stdin.readline
N = int(input())
Nodes = [0] + list(map(int, input().split())) 
Tree = [[] for i in range(N + 1)] 
dp = [[0] * 2 for i in range(N + 1)]
visit = [False for i in range(N + 1)]
num = [[[], []] for i in range(N + 1)]

def dfs(start):
    visit[start] = True
    dp[start][0] = Nodes[start]
    num[start][0].append(start)
    for i in Tree[start]:
        if not visit[i]:
            dfs(i)
            dp[start][0] += dp[i][1]
            for j in num[i][1]:
                num[start][0].append(j)
            if max(dp[i][1], dp[i][0]) != dp[i][1]:
                dp[start][1] += dp[i][0]
                for k in num[i][0]:
                    num[start][1].append(k)
            else:
                dp[start][1] += dp[i][1]
                for k in num[i][1]:
                    num[start][1].append(k)
                    
for i in range(N - 1):
    a, b = map(int, input().split())
    Tree[a].append(b)
    Tree[b].append(a)
    
dfs(1)

if max(dp[1][0], dp[1][1]) == dp[1][0]:
    print(dp[1][0])
    result = num[1][0]
    result.sort()
else:
    print(dp[1][1])
    result = num[1][1]
    result.sort()
    
print(*result)