Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

31. 트리에서의 동적 계획법

트리에 동적 계획법을 적용해 봅시다.

Java / Python

3. 사회망 서비스(SNS)

2533번

이것도 일반적인 그래프에서는 NP-하드입니다.

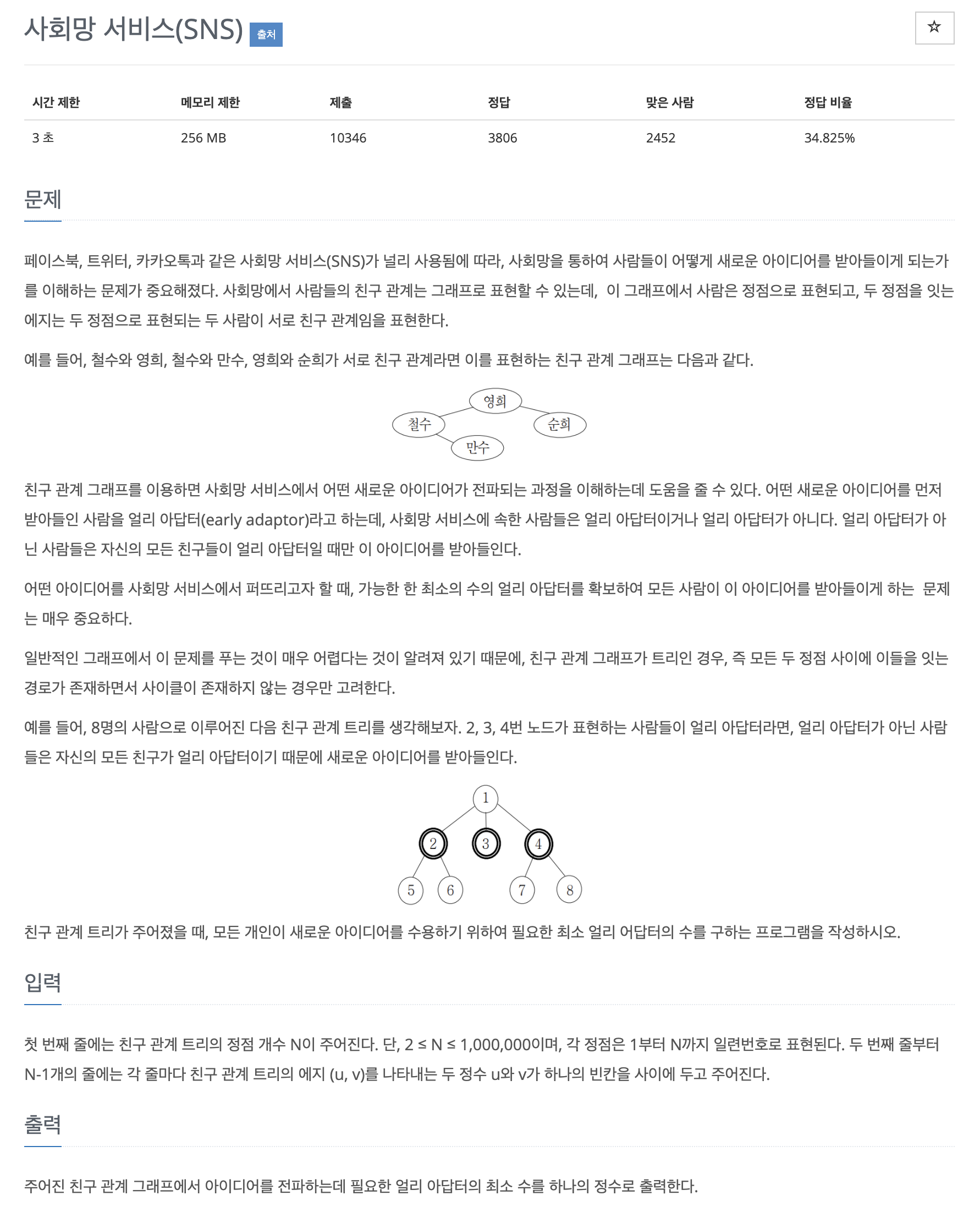
이번 문제는 친구 관계 트리가 주어졌을 때, 모든 개인이 새로운 아이디어를 수용하기 위하여 필요한 최소 얼리 어답터의 수를 구하는 프로그램을 작성하는 문제이다.

DFS를 이용해 가장 아래 노드부터 차례대로 노드가 포함된 경우와 포함되지 않은 경우를 구하고 각 경우에 독립집합이 가장 많은 경우를 DP를 이용해 구한다.

• Java

import java.io.*;
import java.util.*;

public class Main {
	static int N;
	static int[][] dp;
	static LinkedList<Integer>[] tree;

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st;

		N = Integer.parseInt(br.readLine());

		dp = new int[N + 1][2];
		tree = new LinkedList[N + 1];

		for (int i = 1; i <= N; i++) {
			tree[i] = new LinkedList<>();
		}

		for (int i = 0; i < N - 1; i++) {
			st = new StringTokenizer(br.readLine());
			
			int u = Integer.parseInt(st.nextToken());
			int v = Integer.parseInt(st.nextToken());
			
			tree[u].add(v);
			tree[v].add(u);
		}

		dfs(1, -1);

		bw.write(String.valueOf(Math.min(dp[1][0], dp[1][1])));
		bw.flush();
		bw.close();
		br.close();
	}

	public static void dfs(int node, int p) {
		dp[node][0] = 0;
		dp[node][1] = 1;

		for (int next : tree[node]) {
			if (next != p) {
				dfs(next, node);
				dp[node][0] += dp[next][1];
				dp[node][1] += Math.min(dp[next][0], dp[next][1]);
			}
		}
	}
}

• Python

import sys
sys.setrecursionlimit(10**9)
N = int(sys.stdin.readline())
tree = [[] for _ in range(N+1)]
visit = [0 for _ in range(N+1)]
dp = [[0,0] for _ in range(N+1)]

for _ in range(N-1):
    u,v = map(int,sys.stdin.readline().split())
    tree[u].append(v)
    tree[v].append(u)

visit = [True for _ in range(N+1)]
def dfs(now):
    visit[now]=False 
    dp[now][0]=1
    dp[now][1]=0
    for i in tree[now]:
        if visit[i]:
            dfs(i)
            dp[now][0] += dp[i][1]
            dp[now][1] += max(dp[i][0],dp[i][1])

dfs(1)
print(N-max(dp[1][0],dp[1][1]))