자료구조

Bas·2022년 7월 5일
0

§ Array
§ Linked List
§ Binary Tree, Binary Search Tree, Red-Black Tree (레드블랙트리는 개념만!)
§ Heap
§ Hash Table, Set, Map
§ Stack
§ Queue
§ Trie
§ Graph (both directed and undirected)

0. 자료구조

  • 논리적 설계 (데이터 모델링)

  • 물리적 설계 (데이터 구조화)

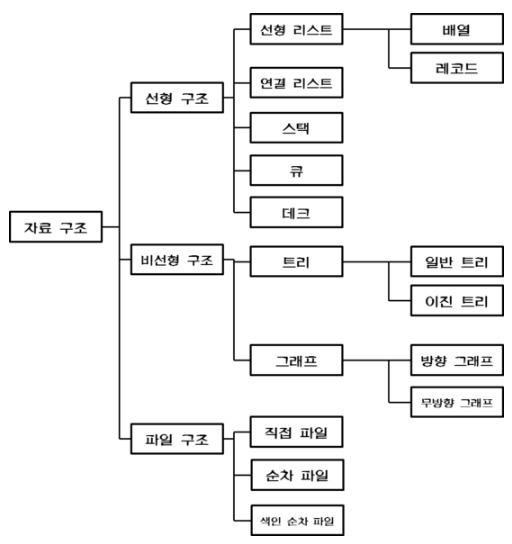
  • 선형 자료구조 (Linear)
    - 하나의 자료 뒤에 하나의 자료가 존재하는 것이다.

    • 자료들 간의 앞뒤 관계가 1:1의 선형관계
    • 배열과 리스트가 대표적이고 더 나아가서 스택, 큐도 이에 해당된다.

  • 비선형 자료구조 (NonLinear)
    - 하나의 자료 뒤에 여러개의 자료가 존재할 수 있는 것이다.
    - 자료들 간의 앞뒤 관계가 1:n, 또는 n:n 의 관계
    - 트리와 그래프가 대표적이며 계층적 구조를 나타내기에 적절하다.

  • 시간 복잡도?
    - '얼마나 빠르게 실행되느냐'

    	- 알고리즘의 로직을 코드로 구현할 때, 시간 복잡도를 고려한다는 것은 '입력 값의 변화에 따라 연산을 실행 할 때, 연산 횟수에 비해 시간이 얼만큼 걸리는가?'라는 말

    • 효율적인 알고리즘을 구현한다는 것 == 입력 값이 커짐에 따라, 증가하는 시간의 비율을 최소화하는 알고리즘을 구성했다는 것

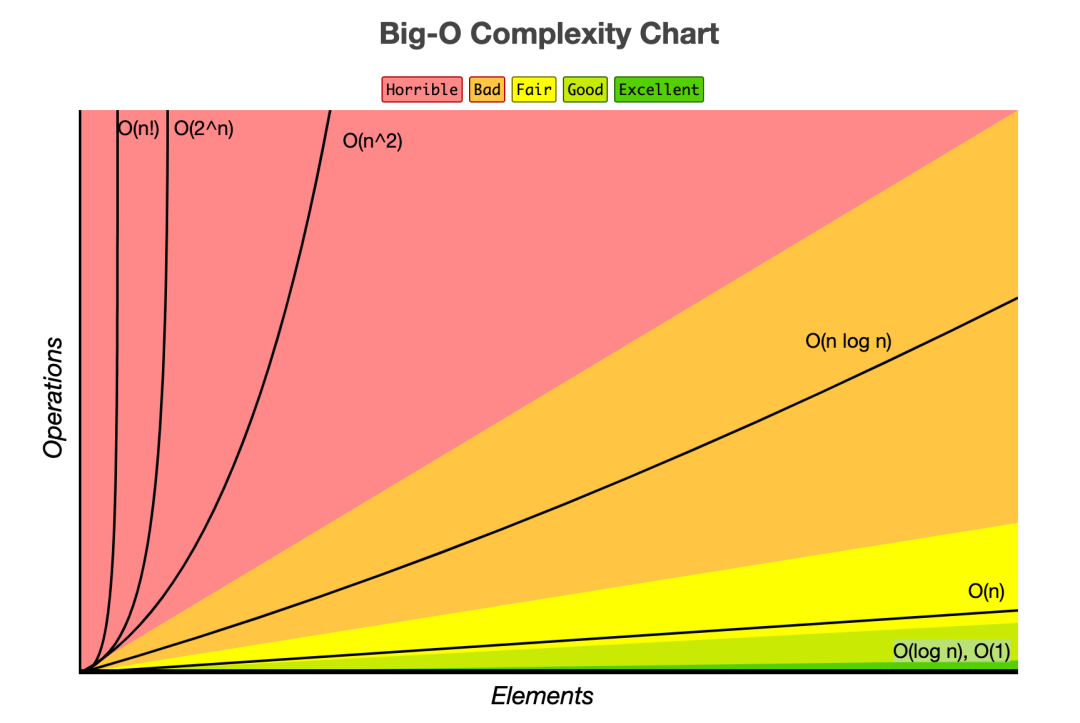
    • 시간 복잡도는 주로 빅-오 표기법을 사용해서 나타낸다.

    • 빅-오 표기법은 최악의 셩우를 고려 하여 , 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있기 때문에 많이 사용된다.

      시간 복잡도 참고 (빅-오, 빅-오메가, 빅-세타)

      Big-O 표기법 종류

  • 공간 복잡도
    - '얼마나 많은 자원이 필요한가?'

=> 좋은 알고리즘? - '시간도 적게 걸리고 자원의 사용도 적어야 하는 것.'
하지만, 시간과 공간은 반비례적인 경향이 있기 때문에 알고리즘의 척도는 시간 복잡도를 위주로 판단합니다.
그러니까 시간 복잡도만 괜찮다면 공간 복잡도는 어느 정도 이해를 해준다는 것! 특히나 요즘과 같은 대용량 시대에는!

  1. 선형 자료구조 (Array, Linked List, stack, queue)

Array

javascript array 시간복잡도

  • 자료구조의 기본
  • 논리적 순서와 물리적 순서가 일치한다.
    -> index를 통해 원소 접근이 용이 (장점)
    -> 삽입/삭제 등에 대한 cost가 높다 (단점)
    -> 순서를 맞추기 위해 뒤의 원소들을 모두 앞으로 shift해줘야한다.
  • 1차원 배열 / 2차원 배열(행렬)
장점: index를 통한 원소 접근 용이
단점: 삽입, 삭제등에 대해 cost높다. 
활용: 
코드 예시:
시간복잡도:  operation별로 나오는게 맞음! -> O(1)
공간 복잡도:
  • 시간복잡도
  • 접근: O(1) 배열 내에서 n번째 index에 해당하는 값 찾아내기
  • 검색: O(n)
  • 추가/삭제: 해당 index를 정확히 알고있다면 O(1)
    index를 찾아야한다면 O(n)
  • 이진 탐색으로 검색: O(logn)

javascript method

Linked List

  • 배열 요소는 메모리에 순차적으로 저장되지만, linked list의 요소는 흩어진 상태로 메모리에 저장된다.-> 메모리를 더 효과적으로 사용할 수 있다.
  • 리스트의 요소는 요소&포인터(참조)의 쌍으로 구성됨.
  • 포인터는 리스트 내의 바로 다음 요소가 저장된 메모리 위치를 가리킨다.
  • Array에서 삽입/삭제 연산의 비효율성을 극복하기위해 나옴
    -> data를 shift해줄필요 x
  • 논리적 순서o , 물리적 순서x

- 단방향 연결 리스트: 마지막 포인터는 null값을 가리키다.
- 양방향 연결 리스트: 데이터를 삭제할 때나 리스트를 양 방향으로 순회할 때 효율적
- 순환 연결 리스트: 마지막 노드는 첫 번째 노드와 연결 (버퍼링-다양한 처리를 원활하게 실행시키려고 버퍼라는 임시 저장 공간에 데이터를 저장하는 작업)에 많이 쓰임

장점: Array 삽입/삭제 비효율성 극복

(모두 노드가 하나 이상인 경우를 기본으로 함)

단방향 연결 리스트
1. head에 새 노드 삽입: O(1) (루프가 필요하지 않음)
2. tail에 새 노드 삽입: O(1) (루프가 필요하지 않음)
3. 중간에 삽입: O(n) - 먼저 n번째 자리를 찾고, 중간에 넣을 것을 n - 1 번째께 가르키도록 해야 하기 때문에 루프가 한번 돈다.
4. 삭제
- head node 삭제: O(1)
- tail node 삭제: O(1)
- 중간꺼 삭제: O(n)
5. 탐색: O(n) - 찾고자 하는 노드가 있다면 head부터 순차적으로 찾아감.

양방향 연결 리스트

  • 두 개의 단계로 나눠짐 (추가할 노드의 포인터를 설정해주는 단계, 양쪽(주변) 노드의 포인터를 설정해주는 단계)
  1. 중간에 삽입: O(n)
  2. 삭제: O(n)
  3. 탐색: O(n)

순환 연결 리스트
새 node가 기존 node를 가리키도록 하고, 새 node를 head로 지정합니다.
tail node가 새 node를 가리키도록 함.
1. head에 추가: O(n) - 위치를 찾아가는 작업이 최대니까
2. tail에 추가: O(n)
3. 중간에 추가: O(n)
4. head 삭제: O(n)
5. tail 삭제: O(n)
6. 중간 삭제: O(n)

Stack

  • FILO(First In Last Out)의 대표적인 예시
  • 활용: 미로찾기, 괄호 유효성 체크 등에 활용
  • 생성 방식에 따른 구별
    - 정적 스택: 데이터 구조의 크기나 규모가 고정
    • 동적 스택: 실행 중 크기를 늘릴 수 있다.
장점: 쉽게 시각화 
단점: 특정 요소를 검색하는 속도를 제한한다.
활용: 역추적이나 문자열을 반전시키는 응용 프로그램 (미로찾기, 괄요 유효성 체크), 함수호출, 스케줄링, 인터럽트 메커니즘 등 다양한 기본 컴퓨닝 프로세스에서 사용
코드 예시:
시간복잡도:
공간 복잡도: 
class Stack {
  constructor() {
    this.arr = [];
  }
  push(item) {
    this.arr.push(item);
  }
  pop() {
    return this.arr.pop();
  }
  peek() {
    return this.arr[this.arr.length - 1];
  }
}

const stack = new Stack();

stack.push(1);
stack.push(2);
stack.push(3);
stack.pop(); // 3
stack.peek(); // 2
stack.peek(); // 2

삽입: 맨 위에 있는거 찾을 때 O(1)
특정 데이터를 찾을 때 O(n)
삭제: O(1)
탐색: O(n)

Queue

  • FIFO(First In First Out - enqueue, dequeue) 구조
  • 활용: 작업 우선순위, Heap
장점:
단점:
활용: 작업 우선순위, Heap 
코드 예시: 순서대로 처리해야하는 작업을 임시로 저장해두는 버퍼로 많이 사용된다.
시간복잡도:
공간 복잡도: 
class Queue {
  constructor() {
    this._arr = [];
  }
  enqueue(item) {
    this._arr.push(item);
  }
  dequeue() {
    return this._arr.shift();
  }
}

const queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
queue.dequeue(); // 1

삽입: O(1)
삭제: O(1)
탐색: O(n)

비선형 자료구조

  • 계층적 구조를 표현하는 자료구조
  • tree, graph가 있다.
  • tree에서 자식 노드는 여러 개의 부모 노드를 가지지 않지만, graph는 자식 노드에 여러 개의 부모 노드가 있는 구조다.

tree

  • 데이터를 삽입, 삭제한다는 것 이전에 표현이 중요.

  • node: 트리를 구성하고있는 원소 그 자체 (key-value기본임? 아니면 이진 탐색에서만 그런거임 ㅡㅡ )

  • edge: node와 node를 연결하는 선

  • root(node): tree에서 최상위 노드

  • terminal(leaf node): tree에서 최하위 노드

  • internal(node): leaf node를 제외한 모든 노드

  • node에는 data를 저장하며, 이때 저장된 데이터를 식별하는데 사용되는 key와 value를 포함할 수 있다.(key-value구조)

  • tree를 탐색하는 과정을 '순회(traversal)'이라고 한다.

1. Binaty tree (이진트리)

  • 가장 많이 사용되는 데이터 구조
  • root node를 포함해서 leaf node를 제외한 모든 노드의 자식이 두 개인 것. (공집합도 노드로 ㅇㅈ)

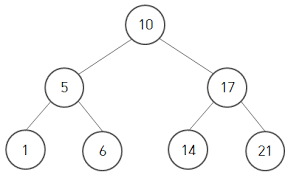
1) binary search tree (이진 탐색 트리)

  • 트리의 node가 key-value로 이루어져있고, 노드의 키를 기준으로 정렬한 상태임.
  • 가장 작은 키를 갖는 노드는 최상위 노드에서 가장 왼쪽에 있는 서브트리 말단에 있고, 가장 큰 키를 갖는 노드는 최상위 노드에서 가장 오른쪽에 있는 서브트리의 말단에 있다.

2) AVL adelson-velsky-landis tree (균형 이진 트리)

  • 어떤 이유로든 존재할 수 있다.
  • 트리의 균형을 조정하는 과정을 거쳐야한다. (왜? -> 메모리 관리를 위해 -> 즉, 균형잡힌 트리는 메모리를 더 효율적으로 사용할 수 있다./성능이 좋다.)
    - 트리의 역할은 유지하되, 가능한 한 최소 높이로 만들어야 함.ㅣ
장점:
단점:
활용: 작업 우선순위, Heap 
코드 예시:
시간복잡도: O(logn)
공간 복잡도:

3) Red Black Tree (rb 이진 탐색 트리)

  • 균형을 조정한다는 점에서 AVL이진 탐색트리와 비슷하지만, 균형을 조정하는 과정에서 트리 회전수가 적어 AVL트리보다 효율적이다.
  • 노드마다 빨강, 검정으로 해석되는 비트를 포함한다는 특징이 있음.
    - 검정: root node는 일반적으로 검정
    • 빨강: 검정 node를 자식 노드로 가진다.
장점:
단점:
활용: 
코드 예시:
시간복잡도: O(logn)
공간 복잡도:

Heap

  • 이진 트리 데이터 구조의 한 종류

  • 값이 최대 혹은 최소인 노드에 빠르게 접근해야하는 응용 프로그램에 적합.

  • 완전 이진 트리의 일종으로, '우선순위 큐'를 위해 만들어진 자료구조입니다.

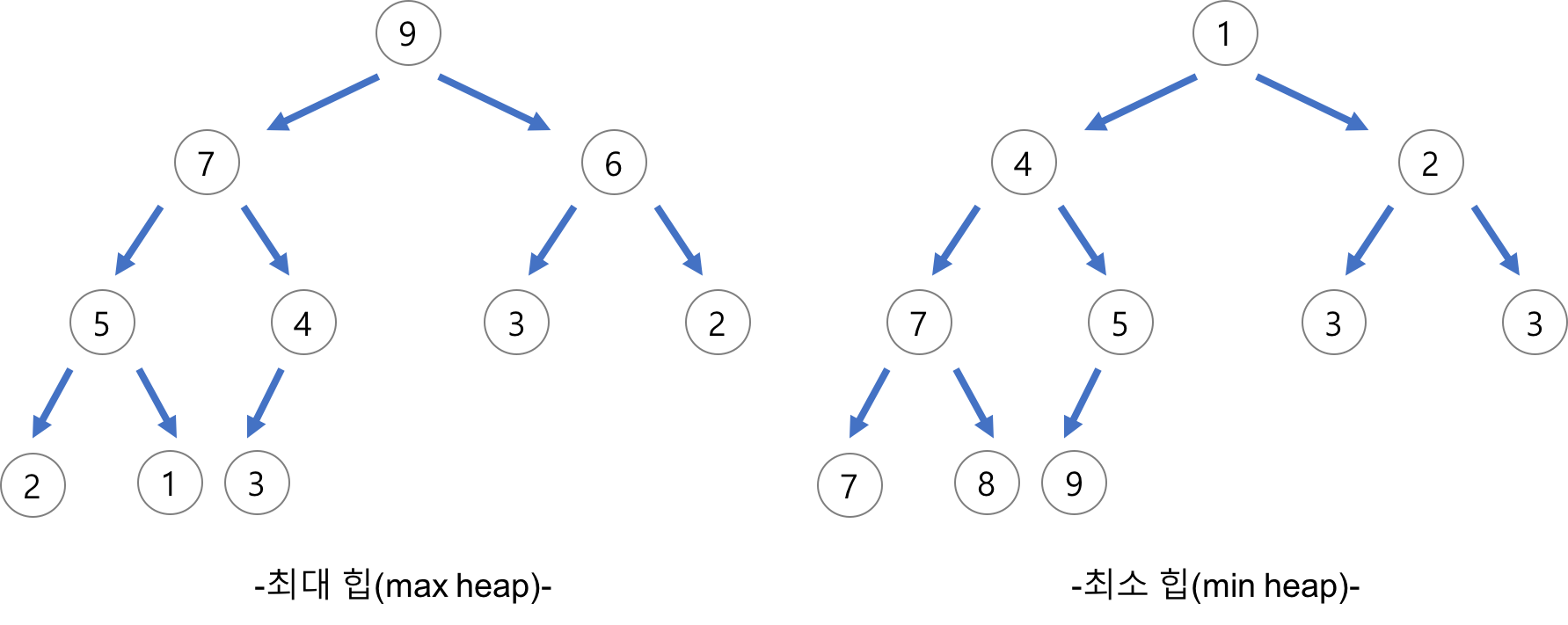
  • 앞에서 먼저 말한 큐는 힙을 사용해서 구현할 수 있으며, 힙의 구조를 설계하ㅡㄴ데는 2가지 방법이 있음. - 최대 힙, 최소 힙

  • 탐색: O(1)

  • 삽입: O(logn)
    1. 힙에 새로운 노드가 들어오면 일단 힙의 마지막 노드에 이어서 삽입한다.

    1. 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.

  • 제거: O(logn)

힙에서의 부모 노드와 자식 노드의 관계
왼쪽 자식의 인덱스 = (부모의 인덱스) 2
오른쪽 자식의 인덱스 = (부모의 인덱스) 2 + 1
부모의 인덱스 = (자식의 인덱스) / 2

priority queue
- 가장 우선순위가 높은 데이터
- 우선순위 큐는 Array, Linked List, Heap으로 구현 가능한데, heap으로 구현하는 것이 가장 효율적이다.
- 우선 순위 Queue를 위해 만들어진 자료구조이다.
- 배열을 이용해서 구현할 수 있다.

Min Heap


class Heap {
  constructor() {
    this.heap = []
  }
  
  // heap 부모-자식 관계
  getLeftChildIndex = (parentIndex) => parentIndex * 2 + 1
  getRightChildIndex = (parentIndex) => parentIndex * 2 + 2
  getParentIndex = (childIndex) => Math.floor((childIndex - 1) / 2)

  
  heapifyUp = () => {
    let index = this.heap.length - 1 // 계속해서 변하는 index 값
    const lastInsertedNode = this.heap[index]

    // 루트노드가 되기 전까지
    while (index > 0) {
      const parentIndex = this.getParentIndex(index)

      // 부모 노드의 key 값이 마지막에 삽입된 노드의 키 값 보다 크다면
      // 부모의 자리를 계속해서 아래로 내린다.
      if (this.heap[parentIndex].key > lastInsertedNode.key) {
        this.heap[index] = this.heap[parentIndex]
        index = parentIndex
      } else break
    }

    // break 를 만나서 자신의 자리를 찾은 상황
    // 마지막에 찾아진 곳이 가장 나중에 들어온 노드가 들어갈 자리다.
    this.heap[index] = lastInsertedNode
  }


 insert = (key, value) => { // 우선순위를 비교하기 위해서 key, value 로 받는다.
    const node = { key, value } // 객체로 node 를 만들고
    this.heap.push(node) // push 한다.
    this.heapifyUp() // 배열에 가장 끝에 넣고, 다시 min heap 의 형태를 갖추도록 한다.
  }
 
 heapifyDown = () => {
    let index = 0
    const count = this.heap.length
    const rootNode = this.heap[index]

    // 계속해서 left child 가 있을 때 까지 검사한다.
    while (this.getLeftChildIndex(index) < count) {
      const leftChildIndex = this.getLeftChildIndex(index)
      const rightChildIndex = this.getRightChildIndex(index)

      // 왼쪽, 오른쪽 중에 더 작은 노드를 찾는다
      // rightChild 가 있다면 key의 값을 비교해서 더 작은 값을 찾는다.
      // 없다면 leftChild 가 더 작은 값을 가지는 인덱스가 된다.
      const smallerChildIndex =
        rightChildIndex < count && this.heap[rightChildIndex].key < this.heap[leftChildIndex].key
          ? rightChildIndex
          : leftChildIndex

      // 자식 노드의 키 값이 루트노드보다 작다면 위로 끌어올린다.
      if (this.heap[smallerChildIndex].key <= rootNode.key) {
        this.heap[index] = this.heap[smallerChildIndex]
        index = smallerChildIndex
      } else break
    }

    this.heap[index] = rootNode
  }
 
  remove = () => {
    const count = this.heap.length
    const rootNode = this.heap[0]

    if (count <= 0) return undefined
    if (count === 1) this.heap = []
    else {
      this.heap[0] = this.heap.pop() // 끝에 있는 노드를 부모로 만들고
      this.heapifyDown() // 다시 min heap 의 형태를 갖추도록 한다.
    }

    return rootNode
  }
  
  peek = () => this.heap[0] // 항상 최상위 노드가 peek 가 된다.
}
장점:
단점:
활용: 전체 자료를 정렬하는 것이 아니라, 가장 큰 값 몇개만 필요할 때,  - 시뮬레이션 시스템, 네트워크 트래픽 제아, 운영체제에서의 작업 스케쥴링, 수치 해석적인 계산
코드 예시:
시간복잡도: 힙 트리의 전체 높이가 거의 log₂n(완전 이진 트리이므로)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 log₂n만큼 소요된다. O(log₂n)
공간 복잡도:

full binary tree (포화 이진 트리)

  • 모든 level이 가득 참

complete binary tree (완전 이진 트리)

  • 왼쪽에서 오른쪽으로 순서대로 채워진 트리

https://www.npmjs.com/package/node-btree

B tree

  • 데이터베이스 시스템을 설계할 때 사용하는 데이터구조로, 자체적인 균형 조정 기능을 갖춘 트리유형
  • 그러나 이진 탐색 트리와 달리 자식 노드를 3개 이상 갖는 부모 노드가 있다.

Tree traversal(트리순회)

선형 자료구조는 순차적으로 요소에 접근하지만 트리 자료구조는 다른 방식을 사용해야한다.

  1. 전위 순회
    - 제일 먼저 root node 방문
    - 루트노드 - 왼쪽 서브트리 - 오른쪽 서브트리
    - 각 서브트리의 root node에 접근

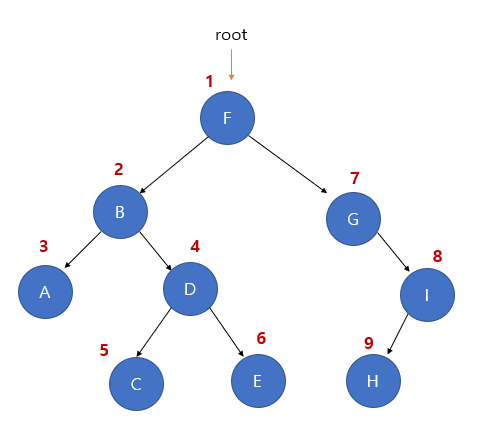
    -> F B A D C E G I H

  2. 중위 순회

    • 중간에 root node를 방문
    • 왼쪽 노드가 있는지 확인하고 더이상 없으면 root -> 오른쪽

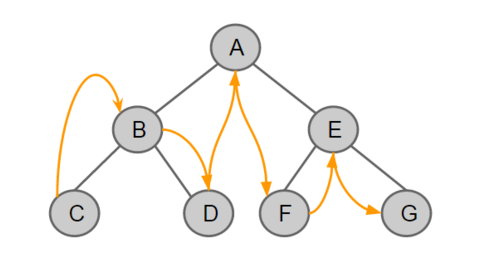
      -> C B D A F E G

  3. 후위 순회
    - root node를 마지막에 접근하는 순회방법.
    - 왼쪽 서브트리 - 오른쪽 서브트리 - 루트노드

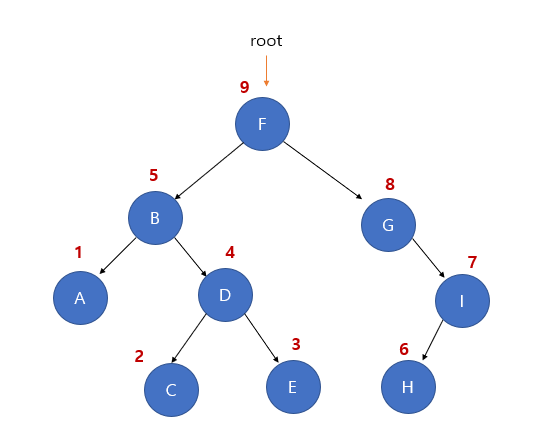
    -> A C E D B F H I G F

1. F의 왼쪽 서브트리 탐색
2. B의 왼쪽 서브트리 탐색
3. A노드 방문
4. B의 오른쪽 서브트리 탐색
5. D의 왼쪽 서브트리 탐색
6. C노드 방문
7. D의 오른쪽 서브트리 탐색
8. E노드 방문
9. D노드 방문
10. B노드 방문
11. F의 오른쪽 서브트리 탐색
12. G의 오른쪽 서브트리 탐색
13. I의 왼쪽 서브트리 탐색
14. H노드 방문
15. I노드 방문
16. G노드 방문
17. F노드 방문
출처: https://code-lab1.tistory.com/9 [코드 연구소:티스토리]

Hash Table

  • 키와 값으로 구성 된 검색 시스템

  • 해시 테이블에는 모든 키에 대응하는 값이 있다. (->시간 복잡도 O(1), 장점) 이런 데이터구성은 검색 수행 속도를 크게 증가시킨다.

  • 어떤 문자열을 넣으면 -> 해시함수는 index와 key-value를 생성한다. 그런데 이 방식은 효율적이지마 해시 값과 배열 크기 때문에 해시 충돌이 발생할 가능성이 있다. 이를 방지하기 위해 체이닝(단순한 배열이 아닌 'linked list'안 배열애 저장하는 방식) 으로 해시 테이블을 구현한다.

  • 해싱 vs 암호화

  • 암호화: 뒤죽박죽 섞어서 읽을 수 없게 만든 후 key가 있는 사람만 정보를 사용할 수 있게함. 이 과정에서 암호화 알고리즘을 사용해서 정보를 암호화-복호화 하는 것을 전제로 함. -> 양방향

  • 해싱: data를 입력받아 고정 길이의 출력을 생성 + 원래의 데이터가 필요하지 않음. -> 단방향

장점:
단점:
활용: 디지털 서명->data의 유효성 검증 -> 수신 된 data가 누구에게서 왔는지 확인, 사용자 인증 ...
코드 예시:
시간복잡도: O(1)
공간 복잡도:

Graph

  • tree보다 현실 세계에 존재하는 연결 관계를 더 잘 표현한다.
  • 그래프의 노드를 보통 '객체'또는 '정점'이라고 함.
  • 정점을 연결하는 선은 'edge'
  • 그래프에서 정점 하나에서 다른 정점으로 가면 edge를 따라가는데, 이를 '경로'
  • 에지가 정점 하나에서 시작해서 해당 정점으로 이어지는 형태를 '루프loop'라고 한다.(첫 번째 정점과 마지막 정점 일치)

Directed Graph (유향 그래프)

  • 노드에서 노드로 방향성을 가진다.edge에 화살표가 있어서 쉽게 식별할 수 있다.(한 방향)

Undirected Graph (무향 그래프)

  • 방향성이 없는 에지를 가진 그래프

가중치 그래프 (유향/무향)

https://helloworldjavascript.net/pages/282-data-structures.html

https://im-developer.tistory.com/121

heap 설명 오지게 잘되어있음

힙 설명 잘되어있음

profile
Bas
바스버거
이전 포스트

1. two sum

다음 포스트

Sorting (버블, 선택, 삽입)

0개의 댓글