1. 버블소트

code

// 버블소트
const bubbleSort =(arr)  => {
  for (let i = 0; i< arr.length - 1; i++) {
    // 루프1: 전체 범위 설정 (두 개씩 잡아서 바꾸기때문에 length-1 해도 됨)
    let swap;
    
    // 루프2: 첫 번째 루프에서 가장 큰 요소는 맨 두로 간다.
	// i, 즉 위치가 확정된 애들은 빼준다.
        for (let j = 0; j < arr.length - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        // 바꿔주는 부분!
        swap = arr[j];
        arr[j] = arr[j+1];
        arr[j+1] = swap;
      }
    }
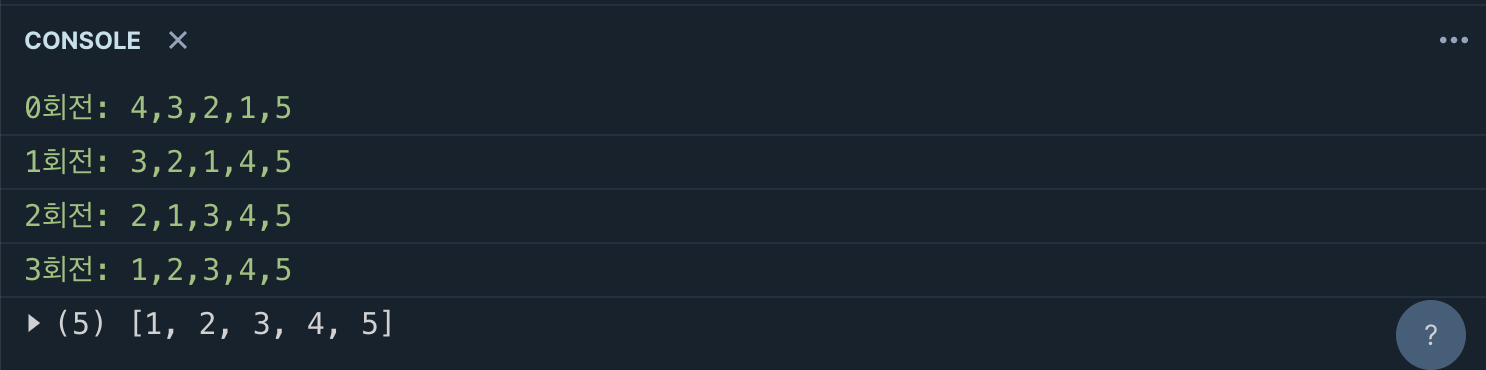
      console.log(`${i}회전: ${arr}`);
  }
   return array;
}

console.log(bubbleSort([5, 4, 3, 2, 1]));

정리

1. inner 루프가 돌 때, 큰 숫자가 오른쪽으로 이동
2. outer 루프가 돌 때, element 하나의 최종 위치(맨 뒤부터) 확정
3. 탐색 범위
   • outer: 0 -> n-1
     - 마지막 element는 이미 비교 되었음.
   • inner: 0 -> n-i-1
     - 이미 정렬 되어있는 부분 제외
4. 시간복잡도
   - worst O(n^2)
   - average O(n^2)
   - best O(n^2)
   (그로나 이미 정렬 된 경우에는 n - 한 번의 순회로 정렬 여부를 알 수 있다.)

장점

• in place 알고리즘으로 메모리가 절약된다.
  -in place: 자료를 정렬할 때 추가적인 메모리 공간이 필요하지 않고, 데이터가 저장된 그 공간 내에서 정렬한다는 뜻.

단점

• 자료의 개수가 많아질수록 성능이 떨어진다.

추가

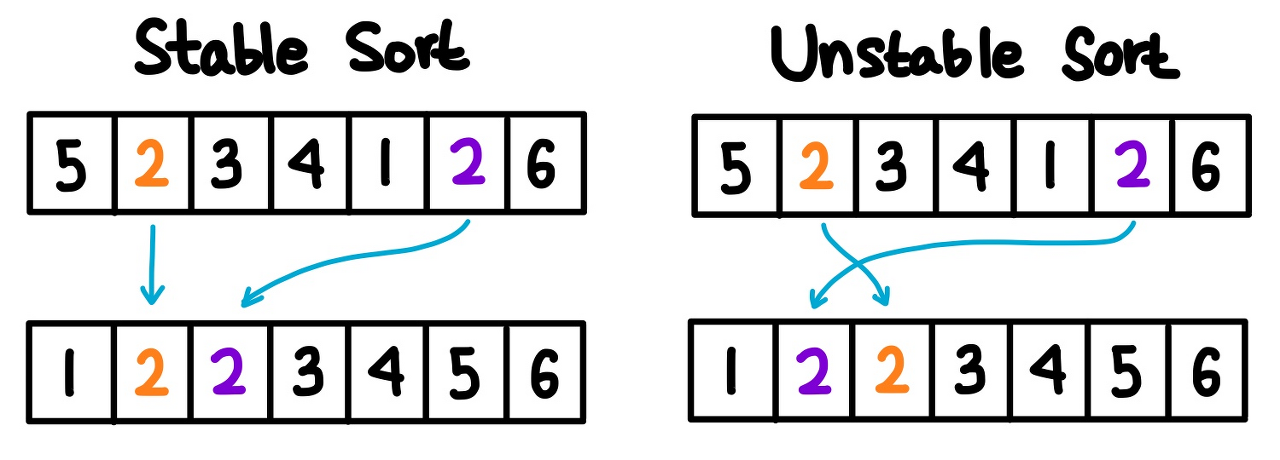
1. Stable한 정렬
   버블정렬은 중복 데이터가 있을 경우, 데이터 위치를 교환하지 않고 지나가는 stable 정렬이다.
   즉, 중복 데이터가 있는 경우에 기존 중복데이터의 순서가 정렬이 다 끝난 이후에고 유지된다.
   

2. 셀렉션소트/선택정렬

• 가장 작은 숫자를 차례로 탐색해서,
• 가장 왼쪽 자리부터 스왑
• 버블소트랑 달리 제일 작은(큰)숫자부터 왼쪽부터 정렬된다.

code

const selectionSort = (arr) => {  
  // 1. 첫 번째 루프에서 범위를 잡는다.
  for (let i = 0; i < arr.length; i++) {    
    // 비교해야 할 최소값 지정
    let minIndex = i;     
    
    // 2. i+1 부터 -> 최소값으로 정렬된 애 '다음'index부터 시작
    // arr.length -> 모든 element를 다 본다.
    for (let j = i + 1; j < arr.length; j++) { 
      if (arr[minIndex] > arr[j]) {        
        // 아직 swap을 하지 않고 기억
        minIndex = j;
            }    
          }
          
          // 2. swap
          if (minIndex !== i) {      
            let swap = arr[minIndex];      
            arr[minIndex] = arr[i];      
            arr[i] = swap;    
          }    
          console.log(`${i}회전: ${arr}`);  
        }  
       return arr;
	}
      
console.log(selectionSort([5, 4, 3, 2, 1]));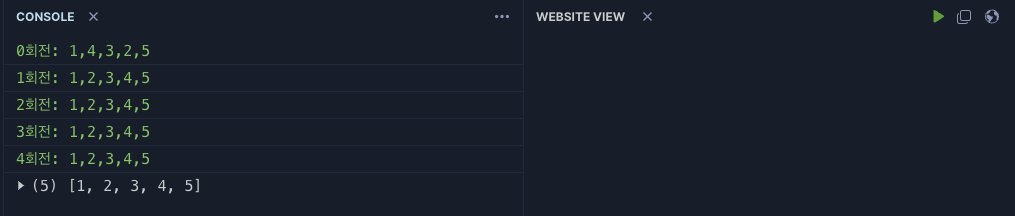

정리

1. 제일 작은(큰) 숫자를 찾기 위해 순차적으로 이동
2. outer 루프가 한 번 돌때마다 element 하나의 최종위치(앞부터)가 확정
3. 탐색범위
   • outer: 0 -> n-1
     - 첫 번째 element를 가장 작은 min숫자로 가정하고
   • inner: 0 -> i+1
     - 이미 정렬 되어있는 부분은 제외
     • 가장 작은 숫자 다음 index부터 비교하며 swap!
4. 시간복잡도
   • worst, average, best O(n^2)

장점

• inplace 알고리즘이라 메모리가 절약된다.

기타

1. UnStable

• 선택 정렬은 데이터가 중복된 경우 위치가 바뀔 수 있기 때문에 Unstable한 정렬이다. 
  

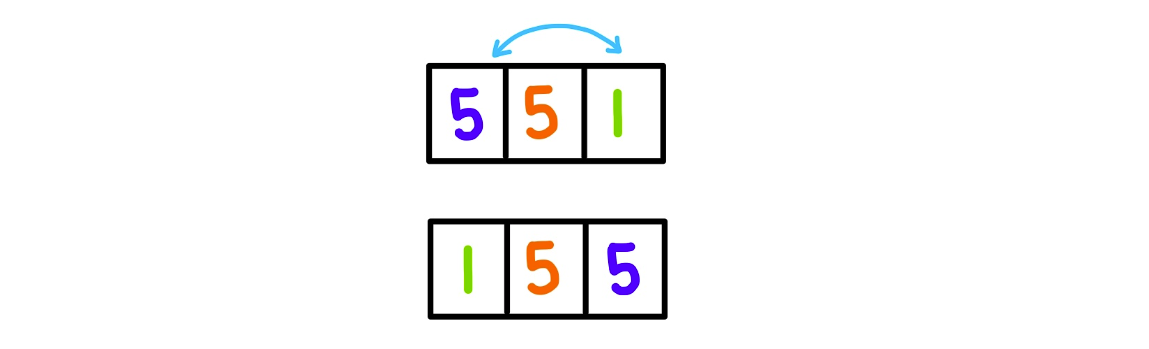
위의 그림을 살펴보면 첫 번째 회전 시에 5가 있는 0번째 칸에 위 리스트의 최소값인 1이 들어가야하므로
1과 5를 교환해야하고 그러면 중복 데이터인 5의 순서가 변하는 것을 알 수 있다.

출처: https://im-developer.tistory.com/133 [Code Playground:티스토리]

3. 삽입정렬

• 버블/선택 정렬과 다르게 한 번 돌때마다 최종 위치가 확정되지 않는다.
  - (그러나 앞에 j 앞에 있는 배열은 정렬이 되었다고 가정!)
• 크기를 하나씩 늘려가면서 정렬(?)
• 정렬 된 array를 유지하면서 진행.
• 즉, 새로운 숫자가 삽입되면, 정렬된 array안에서 자기의 자리를 찾아가면서 정렬

code

const insertionSort = (arr) => {  
  // 1. arr.length 끝까지. 
  // 삽입정렬은 두 번째 요소를 왼쪽 요소(j)와 비교하면서 시작히기떄문에 arr길이가 2개인 상태로 시작
  for (let i = 1; i < arr.length; i++) {    
    
    // i로 현재 정렬된 arr의 사이즈를 알 수 있다.
    let key = arr[i];
    let j = i - 1; // 파고들 준비!

    // 2. 들어가는 값 j와 그 앞의 정렬 된 element를 비교해가면서 루프
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];      
      j--;    
    }

    arr[j + 1] = key;    
    console.log(`${i}회전: ${arr}`);  
  }  
  return arr;
}


console.log(insertionSort([5, 4, 3, 2, 1]));

정리

1. 정렬된 부분적인 어레이를 유지하면서, 한 칸씩 늘려가며 정렬

2. 한 칸 늘릴 때, 새로 삽입 된 데이터를 정렬된 array에서 맞는 자리로 위치시킨다.

3. 탐색범위

   • outer: 1 -> n
     - 정렬된 array를 유지할 때 시작 사이즈를 2로 설정
   • inner: j -> 0 && arr[j] > current
     - 정렬된 array를 끝까지 탐색을 안했고, &&
     • j보다 current가 더 작으면 왼쪽으로 이동

장점

• inplace 알고리즘이라 메모리가 절약된다.

기타

1. Stable

• 삽입 정렬도 중복된 데이터는 위치를 교환하지 않기 때문에 stable한 정렬이다