📌 피보나치 수열(효율적으로 풀기)
우리가 흔히 알고 있는 피보나치 수열은 재귀를 이용하여 풀 수 있다. 그러나 토이문제에서 바라는 것은 바로 효율적으로 풀기 였다.
function fibonacci(n) { if( n === 0 ) { return 0; } else if( n===1 ) { retrun 1; } return fibonacci(n-2) + fibonacci(n-1)
이 형태가 가장 기본적인 형태일텐데 효율적으로 푸는 방법이 있다고 했다. 위 코드로만 풀 게되면 테스트케이스는 실행시간을 초과했다는 문구가 떠버린다ㅠ (효율성이 떨어진다는 것 같다)
그래서 다른 식으로 접근해야 했고, 나의 영원한 사수님 구글님을 통해 다른 코드로 접근할 수 있었다.
첫번째 접근 : 0과 1은 고정이다
피보나치 수열을 조금 적어보자.
0,1,1,2,3,5,8,13 ....
위에 적었던 코드 처럼 어떤 인자(=n)를 넣든 고정된 숫자는 0과 1이다.
그러니까 변수 newArr에 [0,1]을 세팅한다.
두번째 접근 : newArr에 0,1 뒤에 나올 숫자들을 처리할 함수 생성
새로운 함수를 만들되 n을 인자로 하는 새로운 함수이며, 이 함수는 앞서 만든 newArr 을 이용할 것이다. newArr의 0번째 인덱스는 0으로 고정이고, 1번째 인덱스는 1으로 고정이다. 요것들은 newArr[0] === 0 그리고 newArr[1] === 1로 나올것이기에 undefined가 나올 수 없다. 그러나 newArr[2] 는 현재 값이 없으므로 undefined가 나온다.
let newFinbonacci = (n) => { if( newArr[n] !== undefined) { return newArr[n] // n이 0이거나 1일 때는 [0,1]을 리턴한다 } // 그렇지 않을 때 }
newArr[n]의 값이 undefined 일 때는(newArr[n]이 값이 없을 땐) 재귀함수를 쓴다.
이제 newArr[n] 의 값이 undefined가 나올 때는 재귀함수를 이용하여 리턴한다.
newArr[n] = newFibonnaci(n-2) + newFibonnaci(n-1)
이후 이 함수 밖 스코프에서 새로 만들어준 함수를 리턴한다.
☑ 체크할 사항
여기서 염두해두어야 할 점은 함수가 호출되는 순간 차례대로 진행되지 않는다는 점이다. 아래를 확인한다.
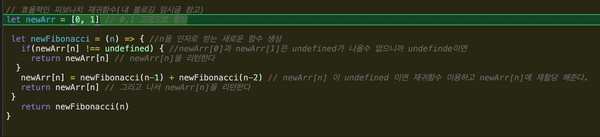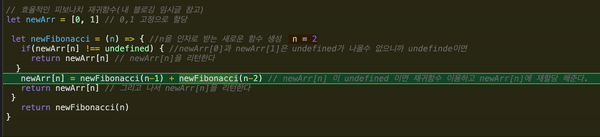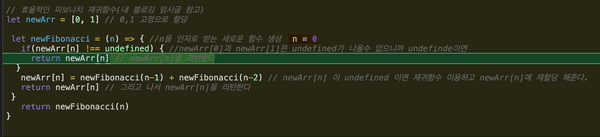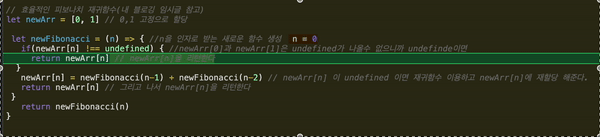
함수를 발견한 순간 가장 아래에 있는 newFibonacci를 실행하고 다시 함수로 돌아간다. 그러면서 재귀를 반복실행한다. n은 0이상의 정수라고 설정해주었기 때문에 n이 0이되면, 0을 리턴하면서 최종종료 한다.
참고
