[백준] BOJ_2293 동전 1 JAVA

BOJ_2293 동전 1

문제

n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.

사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.

---

입력

첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.

---

출력

첫째 줄에 경우의 수를 출력한다. 경우의 수는 2^31보다 작다.

---

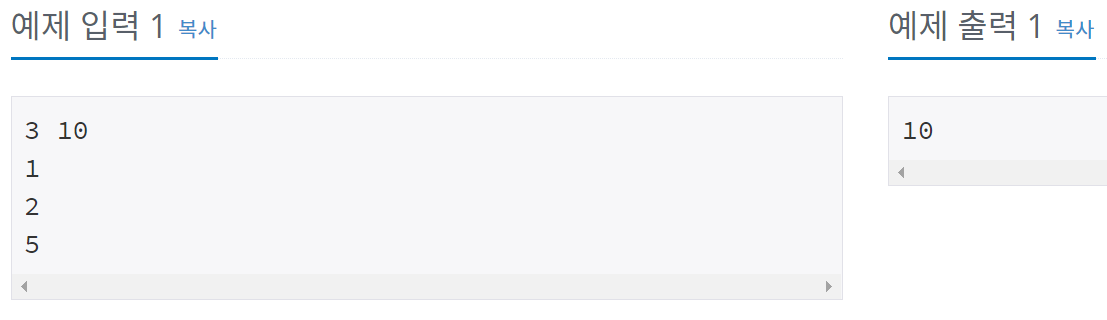
예제 입&출력

---

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    private static int n, k;
    private static int[] coins, dp;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        n = Integer.parseInt(st.nextToken());
        k = Integer.parseInt(st.nextToken());

        coins = new int[n];
        dp = new int[k + 1];
        dp[0] = 1;

        for (int i = 0; i < n; i++) {
            coins[i] = Integer.parseInt(br.readLine());

            for (int j = coins[i]; j <= k; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }

        System.out.println(dp[k]);
    }
}

---

Comment

• solved.ac가 제공하는 나이도 측정은 실버 1 난이도다. 하지만 dp를 채워나갈 점화식을 고안하지 못했다.
• dp[A] = B
  • A : 금액
  • B : A원을 만드는 가능한 경우의 수
• 예를 들어 보자!
  • 2를 만드는 경우의 수
    • 1을 사용해서 2를 만드는 경우의 수는 1+1로 총 1가지 이다.
    • 2를 사용해서 2를 만드는 경우의 수는 2로 총 1가지 이다.
  • 3을 만드는 경우의 수
    • 1을 사용해서 3을 만드는 경우의 수는 1+1+1로 총 1가지 이다.
    • 2를 사용해서 3를 만드는 경우의 수는 1+2로 총 1가지 이다.
  • 4를 만드는 경우의 수
    • 1을 사용해서 4를 만드는 경우의 수는 1+1+1+1로 총 1가지 이다.
    • 2를 사용해서 4를 만드는 경우의 수는 1+1+2, 2+2로 총 2가지 이다.
  • 5를 만드는 경우의 수
    • 1을 사용해서 5를 만드는 경우의 수는 1+1+1+1+1로 총 1가지 이다.
    • 2를 사용해서 5를 만드는 경우의 수는 1+1+1+2, 1+2+2로 총 2가지 이다.
    • 5를 사용해서 5를 만드는 경우의 수는 5로 총 1가지 이다.
  • 이를 통한 결과??
    • 2를 사용해서 5를 만드는 경우의 수를 생각해 보면, 1과 2를 사용해서 3을 만드는 총 경우의 수이다.
    • 즉, A를 사용해서 N를 만드는 경우의 수는 N-A를 만드는 총 경우의 수와 같다.
    • dp[j] = dp[j] + dp[j - coins[i]];

---