P-NP
1.P

출처 - 위키P(PTIME 또는 DTIME(nO(1)))는 결정론적 튜링 기계로 다항 시간 안에 풀 수 있는 판정 문제를 모아 놓은 복잡도 종류이다. 선형 계획 제품, 최대공약수 문제 등이 P에 포함되며, 2002년에는 주어진 숫자가 소수인지 판별하는 문제도 P에 속한
2.NP
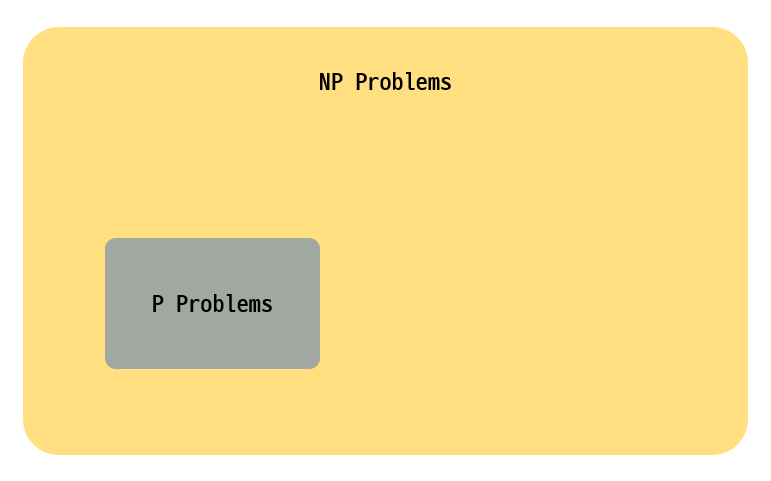
출처 - 위키NP는 비결정론적 튜링 기계(NTM)로 다항 시간 안에 풀 수 있는 판정 문제의 집합으로, NP는 비결정론적 다항시간(非決定論的 多項時間, Non-deterministic Polynomial time)의 약자이다.NP에 속하는 문제는 결정론적 튜링 기계로
3.NP 완전 (NP-complete, NP-C, NPC)
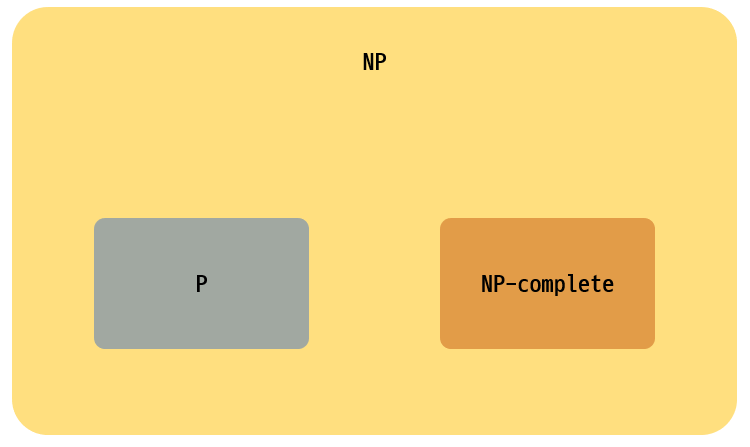
출처 - 위키NP-완전(NP-complete, NP-C, NPC)은 NP 집합에 속하는 결정 문제 중에서 가장 어려운 문제의 부분집합으로, 모든 NP 문제를 다항 시간 내에 NP-완전 문제로 환산할 수 있다. NP-완전 문제 중 하나라도 P에 속한다는 것을 증명한다면
4.NP 난해 (NP-hard)

출처 - 위키NP-난해, NP-hard는 NP에 속하는 모든 판정 문제를 다항 시간에 다대일 환산할 수 있는 문제들의 집합이다. 다시 말하면, NP-난해는 적어도 모든 NP 문제만큼은 어려운 문제들의 집합이다.NP-난해 집합에 속하는 문제가 NP에도 속하면 NP-완전에
5.P-NP 문제

출처 - 위키 >P-NP 문제는 복잡도 종류 P와 NP가 같은지에 대한 컴퓨터 과학의 큰 문제로 컴퓨터로 풀이법이 빠르게 확인된 문제가 컴퓨터로 빠르게 풀리기도 할 것인가 아닌가를 묻고 있다. 1971년 스티븐 쿡이 그의 논문 〈The Complexity of The